Lingkaran Dalam Segitiga - Matematika SMA Kelas XI Kurikulum Merdeka
Summary
TLDRIn this educational video, the concept of the incircle of a triangle is explored, defined as the circle that touches all three sides and is centered at the intersection of the angle bisectors. The video explains how to calculate the radius of the incircle using the relationship between the area of the triangle and its semiperimeter. A step-by-step example illustrates this calculation with a right triangle, detailing how to use the area formula and the sides of the triangle to derive the radius. Viewers are encouraged to practice with provided exercises for better understanding.
Takeaways
- 📐 A circle inscribed in a triangle touches all sides and is centered at the intersection of the angle bisectors of the triangle.
- 🔍 The radius of the inscribed circle is the distance from the center to the sides of the triangle.
- ⚖️ To find the radius, the relationship between the area of the triangle and its semiperimeter is used.
- 📏 The area of a triangle can be calculated using the formula: Area = 1/2 * base * height.
- 🧮 The three smaller triangles formed by the angle bisectors can be used to derive formulas for the radius.
- ⚙️ The formula for the radius of the inscribed circle is: r = Area of triangle / Semiperimeter (S).
- 📊 The semiperimeter (S) is calculated as: S = (a + b + c) / 2, where a, b, and c are the lengths of the triangle's sides.
- 📈 An example of a right triangle is given, with known side lengths used to find the radius of the inscribed circle.
- ✍️ A practical calculation is demonstrated: finding the radius by applying the derived formulas to specific values.
- 🎓 The session concludes with an encouragement to practice further problems to solidify understanding.
Q & A
What is the incircle of a triangle?
-The incircle of a triangle is a circle that lies entirely within the triangle, is tangent to all three sides, and has its center at the intersection of the angle bisectors.
How is the radius of the incircle (r) determined?
-The radius of the incircle is determined using the formula r = A/s, where A is the area of the triangle and s is the semiperimeter.
What is the semiperimeter (s) of a triangle?
-The semiperimeter of a triangle is calculated as s = (a + b + c) / 2, where a, b, and c are the lengths of the sides of the triangle.
How can the area (A) of a right triangle be calculated?
-The area of a right triangle can be calculated using the formula A = 1/2 × base × height.
What formula is used to find the hypotenuse of a right triangle?
-The hypotenuse of a right triangle can be found using the Pythagorean theorem: c = √(a² + b²), where a and b are the lengths of the other two sides.
In the example, what were the lengths of the sides of triangle ABC?
-In the example, the lengths of the sides of triangle ABC were AC = 8 cm, BC = 15 cm, and AB was calculated to be 17 cm.
What was the area of triangle ABC calculated in the example?
-The area of triangle ABC was calculated to be 60 cm² using the formula A = 1/2 × 8 × 15.
How do you find the radius of the incircle for triangle ABC in the example?
-The radius of the incircle for triangle ABC was found using the formula r = A/s, resulting in r = 60 cm² / 20 cm = 3 cm.
What is the significance of the angle bisectors in finding the incircle?
-The angle bisectors are significant because the center of the incircle is located at their intersection, which helps determine the radius and properties of the incircle.
What practice problems are suggested at the end of the video?
-The suggested practice problems involve finding the radius of the incircle for a triangle with sides 5 cm, 12 cm, and 13 cm, and calculating the radius for an equilateral triangle with a side length of 6 cm.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频

Bissetrizes e Incentro - MAT GIO: Matemática com Giovanna

Bisectors of Triangles // GEOMETRY
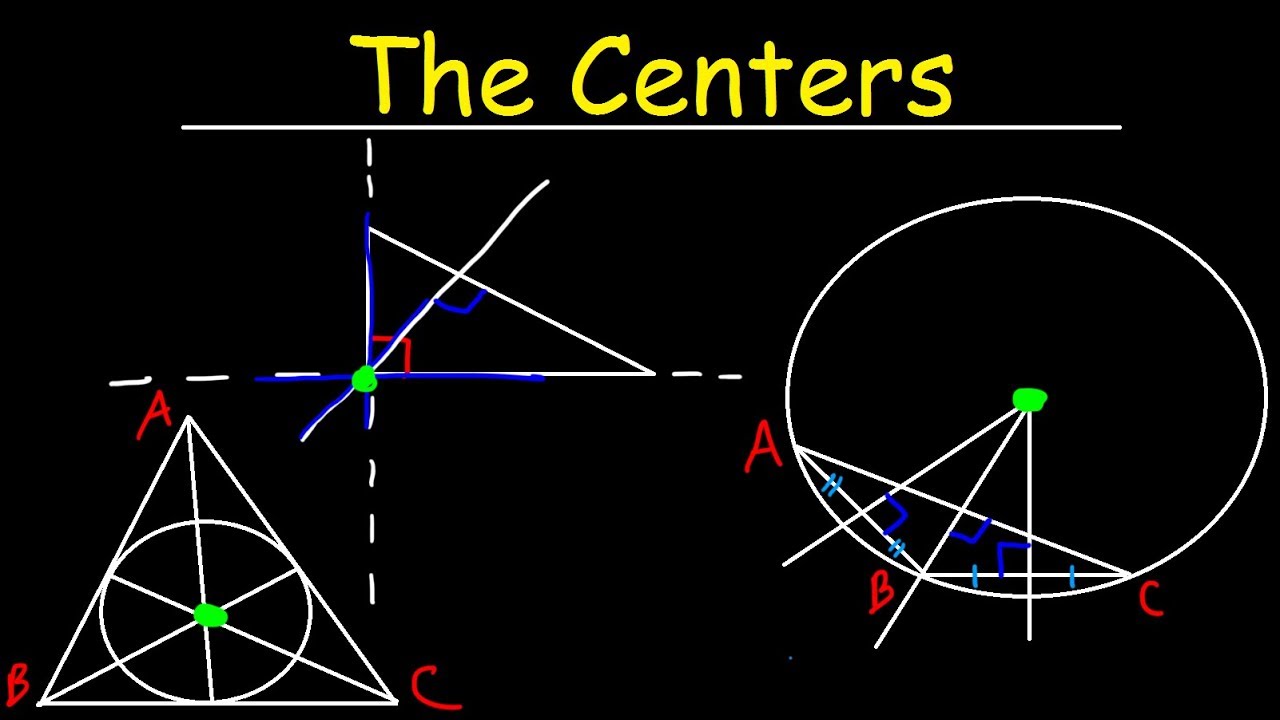
Incenter, Circumcenter, Orthocenter & Centroid of a Triangle - Geometry

LINGKARAN DALAM | LINGKARAN LUAR SEGITIGA | 8 SMP.
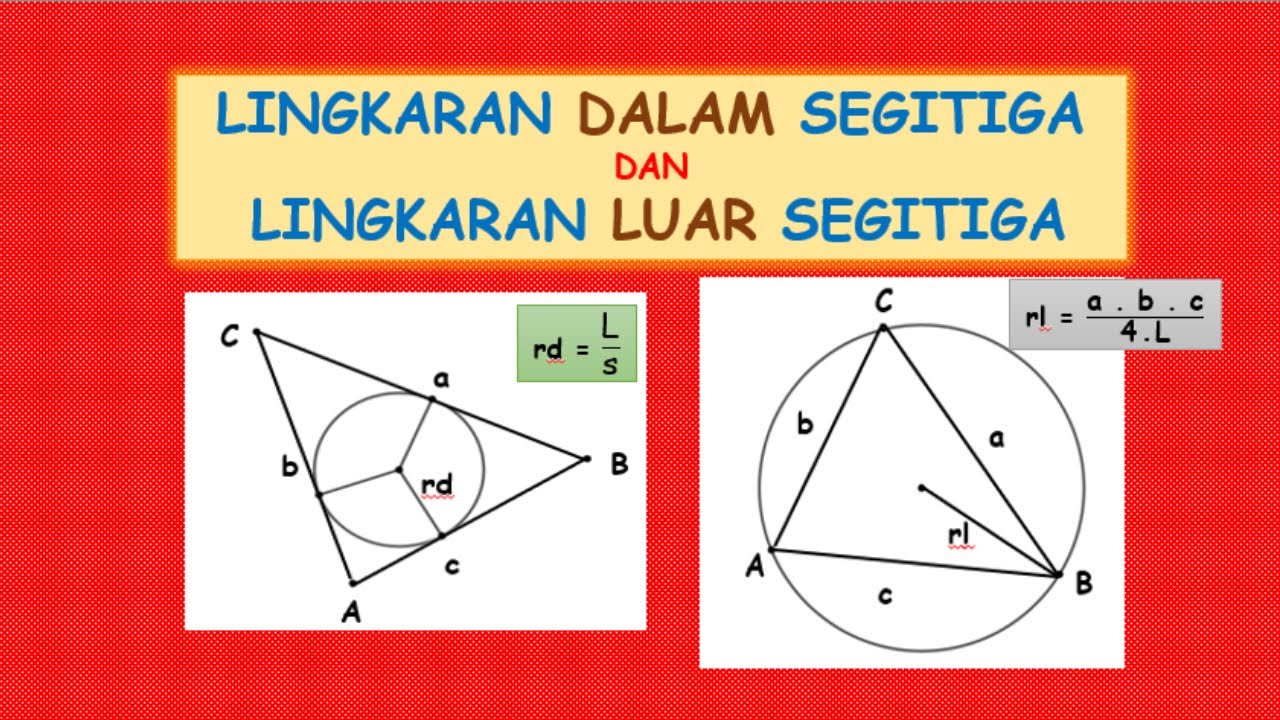
LINGKARAN DALAM SEGITIGA DAN LINGKARAN LUAR SEGITIGA
TRIGONOMETRY 1 (PRECALCULUS) (1 of 54) What Is The Unit Circle?
5.0 / 5 (0 votes)
