Linear Regression in 2 minutes
Summary
TLDRThis script introduces linear regression as a fundamental machine learning technique for prediction. It explains how to use a training dataset to determine a linear function that best fits the data, represented by variables x and y. The process involves finding optimal values for slope (alpha) and intercept (beta) to minimize the sum of squared differences between observed and predicted values. The script also touches on linear regression's simplicity, extensibility, and interpretability, contrasting it with more complex models like neural networks. Finally, it mentions how linear regression can be easily implemented in Python using libraries like scikit-learn.
Takeaways
- 📊 **Prediction Task**: A core task in machine learning is to predict one variable (dependent variable 'y') based on another (independent variable 'x').
- 📈 **Linear Regression**: The simplest form of regression assumes a linear relationship between 'x' and 'y', aiming to find the best fitting line.
- 📉 **Training Data**: A dataset containing values for both 'x' and 'y' is used to train the model and infer the function 'g'.
- 🔍 **Slope and Intercept**: In linear regression, 'alpha' represents the slope and 'beta' the intercept of the line.
- 🧮 **Cost Function**: The fit of the line is quantified by calculating the sum of squared differences between the actual and predicted values.
- 📐 **Optimization**: The goal is to find the values of 'alpha' and 'beta' that minimize the cost function, often done using gradient descent.
- 💻 **Implementation**: Linear regression can be implemented from scratch or using libraries like `scikit-learn` in Python.
- 🔧 **Extensibility**: Linear regression can be extended to handle multiple variables and can be augmented with non-linear features.
- 📊 **Interpretability**: Unlike complex models like neural networks, linear regression coefficients can be easily interpreted.
- 🎯 **Prediction**: Once the model is trained, new 'y' values can be predicted by plugging in new 'x' values into the learned function.
Q & A
What is the primary goal of linear regression in machine learning?
-The primary goal of linear regression in machine learning is to predict the value of a dependent variable (y) based on the value of an independent variable (x) by finding the best-fit linear function.
What is the training data set in the context of linear regression?
-The training data set is a table containing values for both the independent variable (x) and the dependent variable (y) that are used to infer the function g for prediction.
Why is linear regression considered an attractive method for prediction problems?
-Linear regression is attractive because it simplifies the prediction problem by assuming a linear relationship between variables, avoiding the complexity of more sophisticated models like neural networks.
What are alpha and beta in the context of linear regression?
-In linear regression, alpha represents the slope of the line, and beta is the intercept. These are the parameters of the linear function that best fit the training data.
How do you quantify the fit of a line to a set of data points in linear regression?
-The fit of a line to a set of data points is quantified by calculating the sum of the squares of the differences between the actual data points and the points predicted by the line.
What is the process to find the optimal alpha and beta in linear regression?
-To find the optimal alpha and beta, you take the gradient of the sum of squared differences, set it to zero, and solve for alpha and beta to minimize the quantity.
Can linear regression be used to predict the weight of a new person based on their height?
-Yes, once the linear regression model is trained with the appropriate alpha and beta, you can predict the weight of a new person by plugging their height into the formula.
How can linear regression be made more sophisticated without changing its fundamental approach?
-Linear regression can be made more sophisticated by adapting it to fit models with more than one variable as input or by augmenting the data with non-linear features.
What is the advantage of linear regression in terms of interpretability compared to other models like neural networks?
-Linear regression provides interpretable coefficients that can indicate the direction and strength of the relationship between variables, unlike neural networks where the weights are harder to interpret.
How can one implement linear regression without manually deriving the model?
-One can implement linear regression without manual derivation by using libraries like scikit-learn in Python, where you can declare a linear regression model, feed it training data, and use the fit function to train and predict.
What does the term 'extensible' mean in the context of linear regression?
-In the context of linear regression, 'extensible' means that the model can be easily adapted or expanded, for example, by adding more input variables or incorporating non-linear transformations of the data.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级浏览更多相关视频
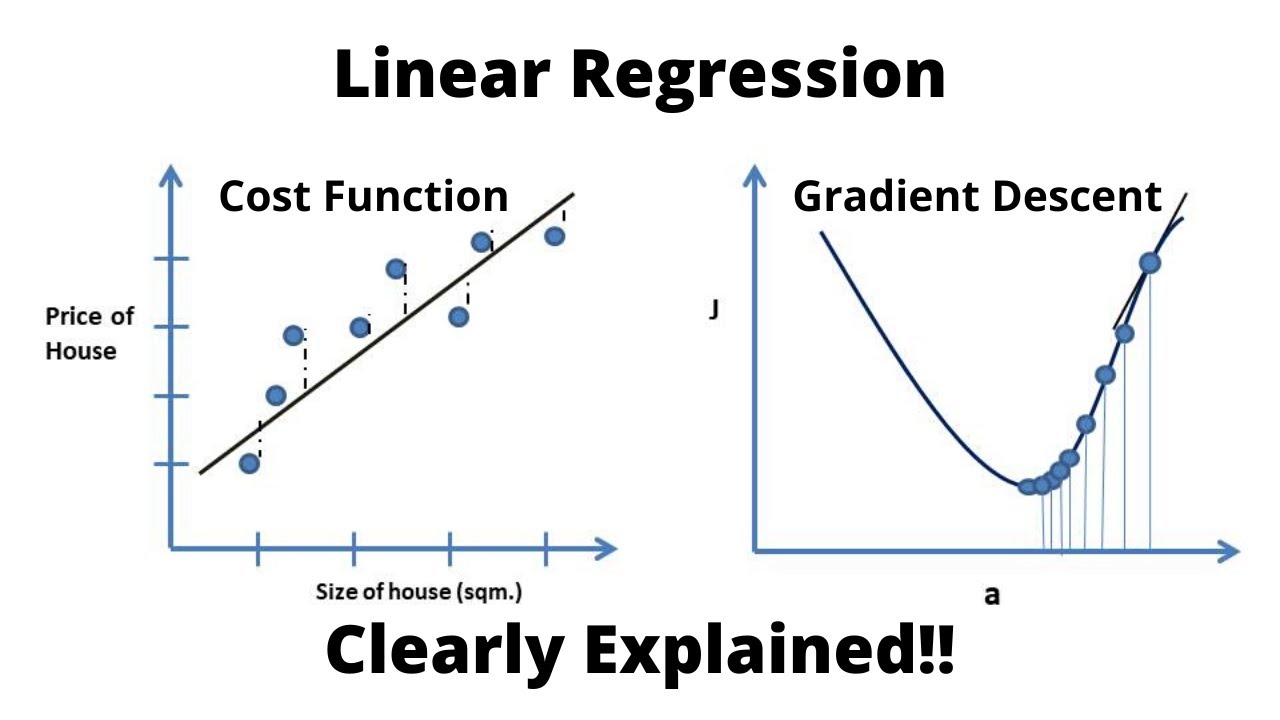
Linear Regression, Cost Function and Gradient Descent Algorithm..Clearly Explained !!

Key Machine Learning terminology like Label, Features, Examples, Models, Regression, Classification

Lec-3: Introduction to Regression with Real Life Examples
3. Learning untuk Klasifikasi dari MACHINE LEARNING

Data Mining 09 - Korelasi & Analisa Regresi (1/2)

Machine Learning Tutorial Python - 8: Logistic Regression (Binary Classification)
5.0 / 5 (0 votes)
