How fractals can help you understand the universe | BBC Ideas
Summary
TLDRThe video explores the concept of fractals, self-similar patterns found in nature and complex systems. It highlights examples like broccoli and snowflakes, and credits Benoit Mandelbrot for coining the term and developing the Mandelbrot set, an infinite fractal visualization. The video suggests fractals' applications in various fields, including climate change, meteorite trajectories, and cancer research, and ponders the possibility of the universe being a fractal. It ends with a teaser about the potential undiscovered uses of fractals.
Takeaways
- 🌌 Galaxies, cloud formations, nervous systems, mountain ranges, and coastlines all exhibit fractal patterns, which are self-similar and infinitely complex.
- 🥦 Broccoli and snowflakes are natural examples of fractals, where smaller parts resemble the whole, highlighting nature's tendency to create unique yet self-replicating structures.
- ❄️ The uniqueness of snowflakes is a result of fractals, where even the smallest differences can lead to entirely new patterns.
- 👨💻 Benoit Mandelbrot coined the term 'fractal' and used IBM's computing power to develop the Mandelbrot set, a visualization of fractals.
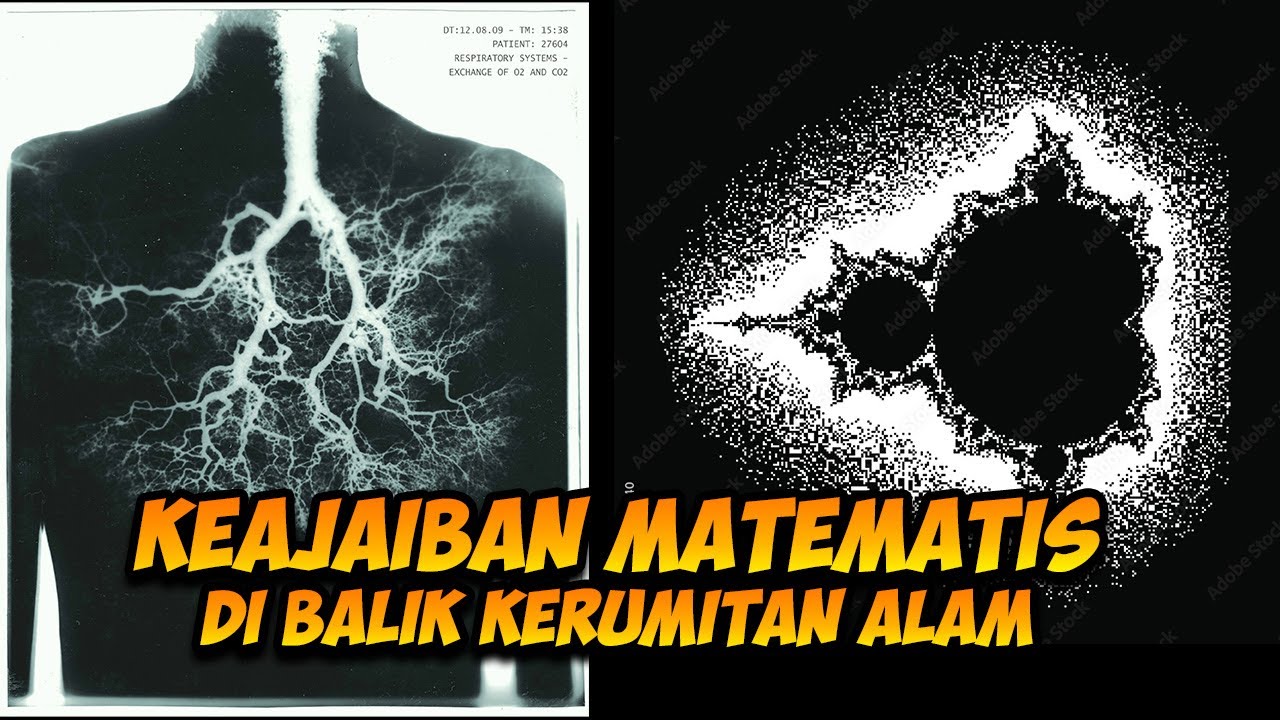
- 🔢 The Mandelbrot set is a breakthrough in mathematics, representing an infinite geometrical pattern that can be magnified indefinitely without repeating.
- 🌐 Fractal geometry has practical applications in various fields, including climate change research, meteorite trajectory analysis, and cancer research by identifying the growth of mutated cells.
- 🌟 Some theories suggest that the universe itself might be a fractal, with structures at every level resembling each other on a smaller scale.
- 🧠 From galaxies to planets, to humans and cells, fractals can be seen at every level of existence, suggesting a deep interconnectedness in the universe.
- 🔬 The exploration of fractals continues to delve deeper into the fabric of reality, from atoms to subatomic particles, hinting at the possibility of an infinitely complex structure.
- 🔮 The full potential of fractals is yet to be discovered, with their complex and mysterious nature promising significant future insights and applications.
Q & A
What is a fractal?
-A fractal is a never-ending pattern that can be found in nature, characterized by self-replicating and unique structures at different scales.
Why are fractals considered important in nature?
-Fractals are important in nature because they explain the continuous creation of new, self-replicating, yet unique structures, and they show how the smallest components are integral to the larger whole.
What is an example of a fractal found in nature?
-Broccoli is a classic example of a fractal in nature, where the whole stalk is a similar version of one of its branches, demonstrating self-similarity.
How do fractals explain the uniqueness of snowflakes?
-Fractals explain the uniqueness of snowflakes by showing that nature works in a way that creates new, self-replicating structures, resulting in infinite variations.
Who coined the term 'fractal' and in what context?
-Benoit Mandelbrot coined the term 'fractal' while working at IBM in 1980, inspired by the mathematical discoveries of the early 19th Century that attempted to define what a curve is.
What is the significance of the Mandelbrot set?
-The Mandelbrot set is significant because it is an infinite geometrical visualization of a fractal, demonstrating that something could be magnified forever, creating infinitely new patterns from the original structure.
How did Mandelbrot's work with IBM contribute to the understanding of fractals?
-Mandelbrot used IBM's computing power to run complex mathematical equations millions of times, leading to the breakthrough equation that combined patterns from previous 'monsters' and resulted in his own set of numbers, the Mandelbrot set.
In what fields is fractal geometry currently applied?
-Fractal geometry is applied in various fields, including climate change research, meteorite trajectory analysis, cancer research to identify mutated cell growth, and even in theories about the structure of the universe.
What is the potential implication of fractals in understanding the universe?
-Some believe that the universe itself may be a fractal, suggesting that if you were to zoom in infinitely, you would find it made up of smaller and smaller self-similar structures.
What are some of the smallest components in the universe that fractals might help us understand?
-Fractals might help us understand components as small as quarks, neutrinos, and potentially even deeper into the fabric of existence, suggesting a continuous structure into infinity.
Why are fractals considered to have a highly complex and mysterious nature?
-Fractals are considered complex and mysterious because they reveal intricate patterns that repeat at every scale, and their applications and implications are still being explored, with many potential uses yet to be discovered.
Outlines

此内容仅限付费用户访问。 请升级后访问。
立即升级Mindmap

此内容仅限付费用户访问。 请升级后访问。
立即升级Keywords

此内容仅限付费用户访问。 请升级后访问。
立即升级Highlights

此内容仅限付费用户访问。 请升级后访问。
立即升级Transcripts

此内容仅限付费用户访问。 请升级后访问。
立即升级5.0 / 5 (0 votes)