Fractals in Nature

Summary

Fractals, the self-repeating patterns found in nature and mathematics, offer profound insights into both the natural world and human innovation. From the growth patterns of leaves and shells to the chaotic structure of galaxies, fractals embody efficient designs driven by recursive processes. These patterns have influenced fields such as biology, engineering, and medicine, with applications ranging from blood vessel growth modeling to advanced material design. With their unique ability to represent complexity in simple forms, fractals continue to inspire technological advancements, promising future breakthroughs in science and design.

Takeaways

• 😀 Fractals are patterns of self-similarity found in nature, ranging from the microscopic scale of leaves to the vast scale of galaxies.
• 😀 Despite their chaotic appearance, natural phenomena like lightning, coastlines, and tree branches exhibit fractal-like self-similarity.
• 😀 The study of fractals has advanced various scientific fields, including computing, telecommunications, biology, and medicine.
• 😀 Fractals can be considered patterns of change, with natural processes like erosion and plant growth often forming fractal structures.
• 😀 Examples of fractals in nature include the nautilus shell, the branching of leaves, and the fractal-like pattern of Romanesco broccoli.
• 😀 Fractals are also present in non-biological structures such as snowflakes, dendrites in metals, and coastal formations.
• 😀 Natural fractals form because of repetitive processes like water erosion or plant growth, creating efficient ways to distribute resources.
• 😀 Fractal patterns are highly efficient in nature, allowing organisms to simplify their structure while maintaining functionality.
• 😀 Human creations, such as town layouts and artwork, have often been subconsciously inspired by fractal patterns.
• 😀 The study of fractals was revitalized by Benoit B. Mandelbrot in the 1970s, who applied them to natural and unnatural phenomena, such as coastlines and the stock market.
• 😀 Fractals have broad applications in modern science, such as in medicine for understanding blood vessel growth, in engineering for fluid dynamics, and in environmental science for modeling porous media and diffusion processes.

Q & A

What are fractals, and how do they appear in nature?

Fractals are repeating patterns in nature that exhibit self-similarity at different scales. They appear in natural objects and processes, such as the branching of trees, the structure of snowflakes, and the growth of leaves on plants, where the same pattern repeats on different levels of detail.

How do fractals relate to chaos in the universe?

Fractals are often associated with chaos due to their complex and seemingly disordered nature. However, they show underlying self-similarity, indicating a higher level of organization within the chaos. For example, the formation of coastlines, clouds, and mountain ranges follows fractal patterns despite appearing random.

How do fractals contribute to the efficiency of natural systems?

Fractals optimize efficiency in natural systems. For instance, the fractal structure of a leaf's veins allows for efficient nutrient and water transport, and the spiral shape of a nautilus shell helps in maximizing space while maintaining structural strength.

Can you explain the role of fractals in the growth of plants?

In plants, fractal patterns help optimize growth. For example, Romanesco broccoli grows in a self-replicating pattern where each bud contains smaller buds, which helps maximize surface area for nutrient absorption, ensuring efficient growth.

What is the Mandelbrot set, and how is it related to fractals?

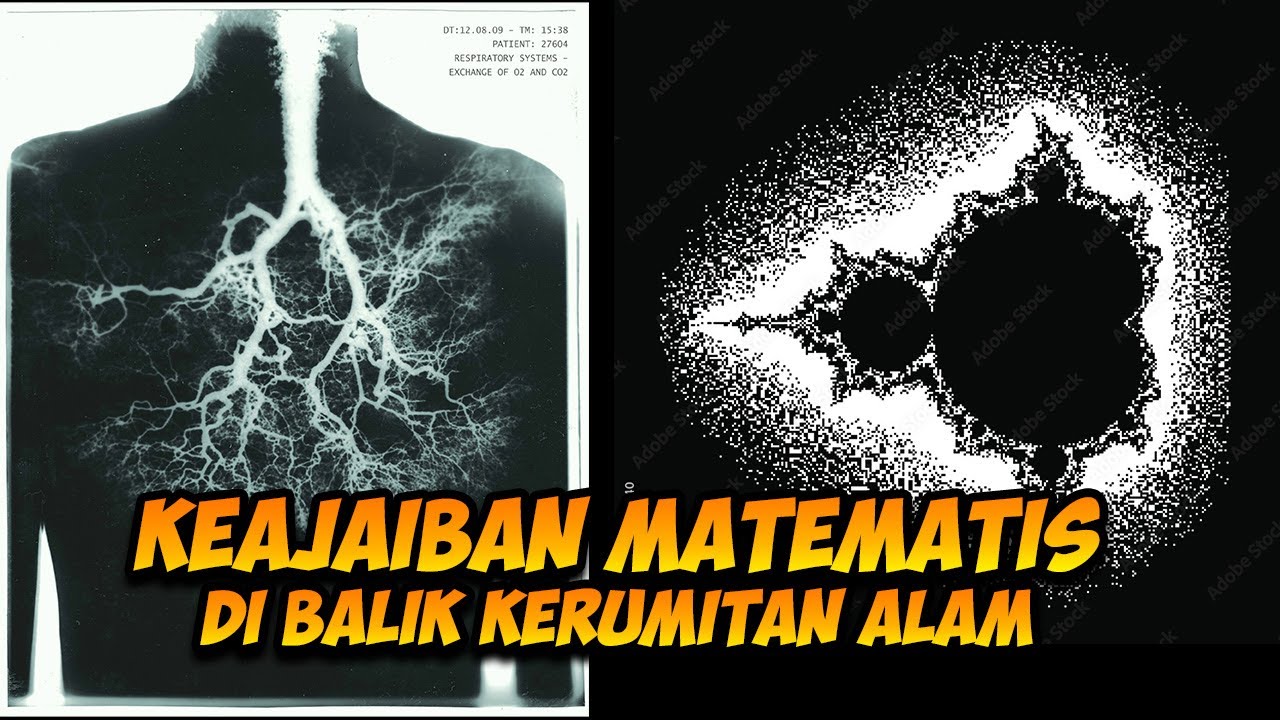
The Mandelbrot set is a famous fractal pattern discovered by Benoit B. Mandelbrot. It is a set of complex numbers that produces intricate, self-similar structures when plotted. Mandelbrot's work advanced the field of fractals and illustrated how they can model natural phenomena like coastlines and even the stock market.

How does fractal geometry differ from traditional geometry?

Unlike traditional geometry, which deals with integer dimensions (1D, 2D, and 3D), fractals have non-integer or Hausdorff dimensions, allowing them to more accurately represent complex, self-similar structures in nature. This ability to represent irregular shapes gives fractals an edge in modeling natural processes.

What role do fractals play in biology and medicine?

Fractals have numerous applications in biology and medicine. For example, the growth of blood vessels follows fractal patterns, and studying these patterns can help detect cancerous tissues. Fractal models are also used to analyze the distribution of plants in forests and the organization of neurons in the brain.

How are fractals applied in engineering and technology?

In engineering, fractals are used to improve designs by optimizing surface areas. They are employed in fields like fluid dynamics, material science, and antenna design to reduce material usage while maintaining or enhancing performance. For example, fractal patterns are applied to cooling units and antenna designs to maximize surface area without increasing size.

What is the significance of fractals in art and architecture?

Fractals have influenced art and architecture by inspiring designs that mirror the self-similar patterns found in nature. The logarithmic spiral, a key feature of fractals, is commonly seen in Renaissance art, and human settlements have often been organized in fractal patterns, reflecting a subconscious understanding of these natural structures.

How has the advent of computing advanced the study of fractals?

The advent of computing in the late 20th century revolutionized the study of fractals. Using computers, mathematicians like Benoit Mandelbrot were able to visualize and explore fractals in ways that were not possible before, leading to the discovery of complex fractal structures such as the Mandelbrot set and applications in various fields like biology, engineering, and economics.