Why trees look like rivers and also blood vessels and also lightning…

Summary

The video explores the fascinating concept of fractals, self-similar patterns found in nature and beyond, such as in trees, rivers, and even our own bodies. It delves into how these patterns maximize efficiency in various systems, from trees absorbing sunlight to our circulatory system delivering nutrients. The video also touches on the mathematical dimensions of fractals and their prevalence in both living and non-living entities.

Takeaways

• 🌳 Fractals are self-similar shapes that repeat their patterns at different scales and are found in both living and non-living things.
• 🔍 The concept of self-similarity is exemplified by parts of a tree resembling the whole tree, a characteristic shared by many natural and artificial structures.
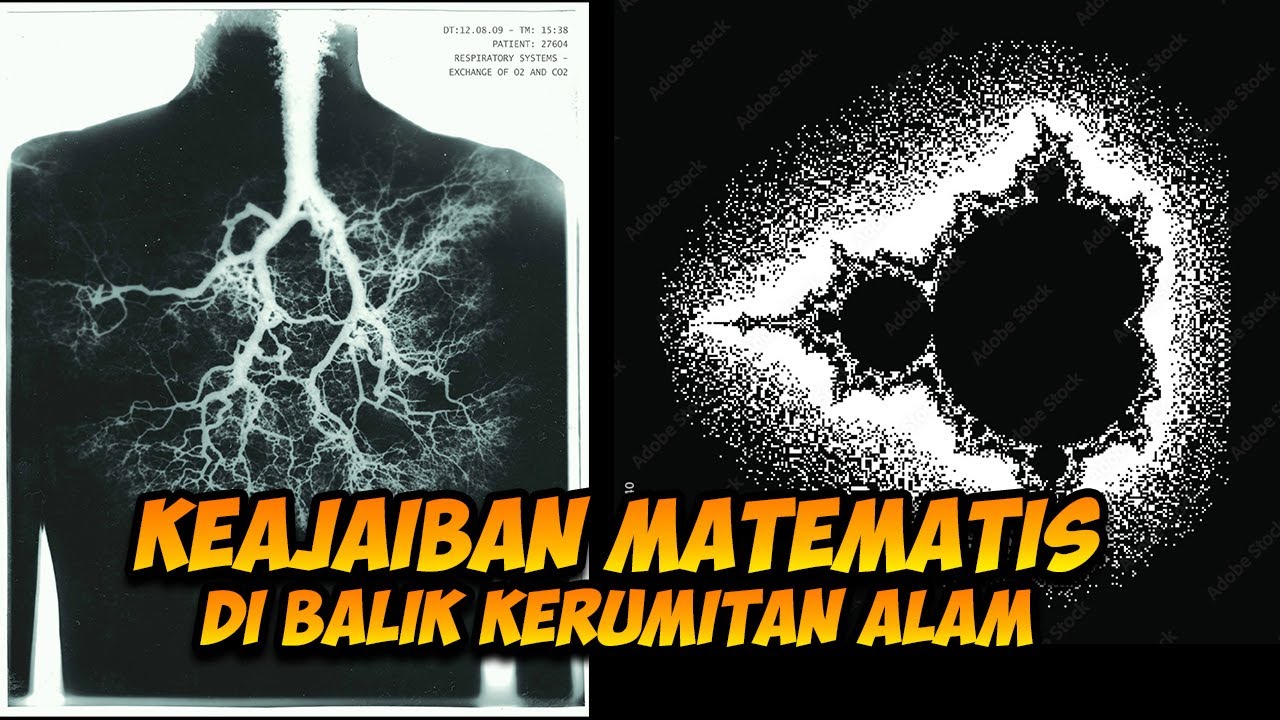
• 🌐 Fractals were named by Benoit Mandelbrot because they exist in 'fractured dimensions', occupying a space between traditional dimensions.
• 📏 The dimension of a fractal is determined by how it fills space when scaled, which can result in non-integer dimensions, like 1.585.
• 🌿 Trees and plants use fractal patterns to maximize surface area for sunlight absorption and nutrient intake without expending unnecessary energy on growth.
• 💨 Fractal branching is efficient for the human circulatory system, allowing a vast network of blood vessels to be packed within the body efficiently.
• 🌪 Rivers naturally form fractal patterns for efficient water drainage from land and sediment distribution at river mouths.
• ⚡ Both cracks and lightning bolts exhibit fractal patterns as they are efficient ways to dissipate energy within a space.
• ❄️ Fractals also appear in non-living phenomena like snowflakes and mineral deposits, influenced by environmental conditions and chemical concentrations.
• 🧬 There isn't a universal rule or gene causing fractal patterns; rather, they emerge as efficient solutions to various natural and biological problems.
• 🤔 The script encourages viewers to stay curious about the fascinating patterns and dimensions in nature and the world around us.

Q & A

What is the concept of self-similarity as mentioned in the script?

Self-similarity is a property of an object where it resembles itself at different scales. It's like a part of a tree looking like a smaller version of the whole tree, which is a characteristic of fractals.

Who is Benoit Mandelbrot, and what did he contribute to the understanding of fractals?

Benoit Mandelbrot was a mathematician who named and popularized the concept of fractals. He described these self-repeating shapes as existing in 'fractured dimensions,' highlighting their unique scaling properties.

What does the term 'fractal dimension' refer to?

Fractal dimension refers to the scaling behavior of a fractal. Unlike traditional dimensions, it can be a non-integer value that indicates how a fractal pattern fills space differently as it scales up or down.

How do trees utilize fractal patterns to their advantage?

Trees use fractal patterns to maximize surface area for absorbing sunlight and CO2 within a finite volume, allowing them to grow efficiently without expending unnecessary energy.

What is the relationship between fractals and the human circulatory system?

The human circulatory system exhibits fractal patterns in the branching of blood vessels, which allows for an extensive network to efficiently deliver oxygen and nutrients throughout the body while minimizing energy expenditure.

Why do rivers form branching patterns?

Rivers form branching patterns as an efficient way to drain water from an area. The fractal branching at the river's mouth is a result of sediment deposition and division of the river into smaller streams.

How do fractals relate to the concept of energy dissipation in natural phenomena like cracks and lightning?

Fractals are the most efficient way to dissipate energy within a given space, which is why patterns like cracks in the ceiling and lightning bolts often exhibit fractal branching.

What is the role of fractals in the growth of crystals and snowflakes?

In the growth of crystals and snowflakes, fractals appear due to repeating rules influenced by factors like temperature, humidity, and chemical concentrations, resulting in self-similar patterns at multiple scales.

Why do different natural systems evolve to exhibit fractal patterns?

Different natural systems evolve to exhibit fractal patterns because they represent an efficient solution to various problems they face, such as maximizing surface area or energy dissipation, without wasting resources.

What is the significance of fractals in understanding the natural world?

Fractals are significant in understanding the natural world because they reveal a common, efficient solution to diverse problems across living and non-living systems, offering a new dimension to observe and analyze natural phenomena.

How can the concept of fractals be applied in the study of nature and science?

The concept of fractals can be applied in the study of nature and science to model and understand complex systems that exhibit self-similar patterns at different scales, such as in the growth of plants, the structure of the circulatory system, and the flow of rivers.

Outlines

00:00

🌳 The Mystery of Self-Similarity in Nature

This paragraph delves into the concept of self-similarity, particularly in the context of trees and other natural and man-made structures. The narrator, Joe, begins by highlighting the uncanny resemblance of a tree's branch to the tree itself, and extends this observation to other entities like blood vessels, rivers, and even cracks in the ceiling. The central theme revolves around the idea that these seemingly disparate objects share a common pattern, which is identified as fractals. Fractals are self-similar shapes that repeat at different scales, a concept introduced by mathematician Benoit Mandelbrot. The explanation further explores how fractals exist in a 'fractured dimension', a notion that deviates from the traditional understanding of dimensions. The paragraph sets the stage for understanding the prevalence and significance of fractals in various natural and biological phenomena.

05:02

🌿 Fractals in Nature: Efficiency in Growth

This paragraph expands on the concept introduced in the first, focusing on the practical applications and benefits of fractals in nature. The narrator discusses how trees, despite their diverse biological classifications, share a common fractal pattern in their growth. This pattern allows trees to maximize surface area for sunlight absorption and CO2 intake, thus optimizing their energy expenditure. The explanation extends to the roots of trees and the human circulatory system, both of which utilize fractal branching to maximize surface area for nutrient and oxygen exchange. The paragraph also touches on the efficiency of fractal patterns in non-living systems, such as river systems and lightning, illustrating how these patterns are not confined to biological entities. The narrator emphasizes that fractals are not just mathematical curiosities but are integral to understanding the efficiency of various natural systems.

10:04

🌐 Fractals Beyond Biology: Universal Patterns in Nature

The final paragraph of the script shifts the focus from biological systems to non-biological phenomena, reinforcing the ubiquity of fractals in nature. The narrator discusses how rivers, cracks, and lightning bolts exhibit fractal patterns, which are efficient means of energy dissipation within a confined space. The explanation also includes the formation of crystals and snowflakes, which, despite being driven by different environmental factors, follow similar fractal patterns. The paragraph concludes by emphasizing that while fractal patterns are widespread, they are not governed by a single universal rule. Instead, various systems have independently evolved these patterns as an efficient solution to their specific challenges. The narrator encourages viewers to stay curious and hints at further exploration of these patterns in a different show called 'Overview'.

Keywords

💡Fractals

Fractals are self-similar shapes that repeat the same pattern at different scales. They are a key concept in the video, illustrating how various natural and artificial structures exhibit similar branching patterns. The video discusses how fractals are seen in trees, rivers, lightning, and even human blood vessels, highlighting their ubiquity and significance in nature and human biology.

💡Self-similarity

Self-similarity refers to the property of an object to be similar to a smaller copy of itself. In the context of the video, self-similarity is a defining characteristic of fractals, observed in the branching patterns of trees and other structures. It is used to explain how parts of a tree or other fractal objects resemble the whole, emphasizing the repeating patterns across different scales.

💡Benoit Mandelbrot

Benoit Mandelbrot was a mathematician who is credited with coining the term 'fractal' and popularizing the study of fractals. His work is central to the video's discussion on fractals, as he introduced the concept of fractal dimensions, which are dimensions that fall between whole numbers, helping to describe the complex geometry of fractals.

💡Dimension

In the video, 'dimension' is used in a mathematical sense to describe how shapes fill space as they scale up or down. Mandelbrot's concept of fractal dimensions is introduced to explain how fractals, like trees and rivers, occupy space in a way that is not strictly one, two, or three dimensions. This concept is crucial for understanding the unique properties of fractals.

💡Branching patterns

Branching patterns are a recurring theme in the video, used to describe the way trees, blood vessels, and rivers form their structures. These patterns are fractal in nature, repeating similar shapes at different scales. The video uses branching patterns to illustrate the efficiency and beauty of fractals in various natural systems.

💡Efficiency

Efficiency is a key concept in the video, as it explains why fractal structures are prevalent in nature. Fractals allow for maximum surface area in a given volume, which is beneficial for processes like photosynthesis in trees or oxygen exchange in lungs. The video highlights how fractal branching is an efficient solution to various biological and environmental challenges.

💡Trees

Trees are used as a primary example in the video to illustrate the concept of fractals. The branching structure of trees, both in their above-ground foliage and below-ground roots, is shown to be fractal. This allows trees to maximize their surface area for photosynthesis and nutrient absorption, making them an excellent example of fractal efficiency in nature.

💡Blood vessels

Blood vessels are mentioned in the video as another example of fractal structures in biology. The circulatory system's branching pattern allows for efficient distribution of oxygen and nutrients throughout the body. The video uses this example to show how fractals are not just a mathematical curiosity but also a fundamental aspect of biological systems.

💡Rivers

Rivers are discussed in the video as an example of fractal patterns in nature. The branching structure of rivers, from their sources to their mouths, is shown to be an efficient way to drain water from an area. The video uses rivers to demonstrate how fractals can be seen in both living and non-living systems.

💡Lightning

Lightning is mentioned in the video as an example of a fractal pattern in nature. The branching paths of lightning bolts are shown to be an efficient way to dissipate energy. This example is used to illustrate how fractals are not limited to static structures but can also describe dynamic processes.

Highlights

The concept of self-similarity in nature, where parts of an object resemble the whole, is highlighted through the comparison of trees and their branches to blood vessels.

Fractals are introduced as self-similar shapes that repeat patterns at different scales, a fascination for mathematicians and beyond.

Benoit Mandelbrot's contribution to the understanding of fractals, naming them for their existence between dimensions.

A mathematical explanation of dimensions in relation to scaling up shapes and the unique dimension concept applied to fractals.

The efficiency of fractal patterns in nature, such as trees, for maximizing surface area for resource absorption without excessive energy expenditure.

The biological reasoning behind why 'trees' as a category are more about appearance than strict biological relation.

The role of fractals in the human body, specifically in the lungs and circulatory system, for efficient gas exchange and nutrient delivery.

Rivers and their natural fractal branching as an efficient means of water drainage and sediment deposition.

The appearance of fractal patterns in non-living phenomena such as cracks and lightning, as an efficient way to dissipate energy.

The modeling of growth patterns in nature that result in fractal dimensions, differing from the traditional understanding of dimensions.

The variety of fractal patterns observed in different natural systems, each evolving to the same efficient solution independently.

The contrast between fractals in nature and those formed through crystallization, which follow different rules but result in similar self-similar patterns.

The absence of a single rule or gene responsible for fractal patterns, suggesting a convergence on efficiency in various natural systems.

A call to stay curious and an invitation to explore more complex and interesting topics in the 'Overview' show on PBS Terra.

An acknowledgment of Patreon supporters as a driving force behind the research and creation of content for the show.

A humorous anecdote about the correct pronunciation of Benoit Mandelbrot's name, adding a light-hearted touch to the end of the video.

Transcripts

- Hey, smart people, Joe here.

Ever notice how if you look at part of a tree,

it looks a lot like an entire tree?

And why does this underground part of a tree

look so much like the rest of the tree?

That's pretty weird.

This isn't a tree, but it sort of looks like one.

And so does this, hmm.

And these branches, sure look an awful lot

like these branches, except those are blood vessels

and so are these, which also kind of look like a tree,

although this part reminds me of a river

or maybe every river?

Lightning, lungs, cracks in the ceiling,

what's going on here?

Why do all these things look so similar?

Once you start seeing it, you see it everywhere.

It haunts your dreams!

It's like there's some spooky connection

between rivers and lightning bolts and broccoli and trees

and all sorts of living and non-living things.

Well, all these objects have one thing in common,

zoom in or out, and we see the same branching pattern

repeat itself over and over at different scales.

These are fractals, a special kind of self-similar shape

that mathematicians, and the rest of us, go extra crazy for.

And this video is about why we see them everywhere.

(pensive music)

I don't know if you've ever looked at a tree

as deeply as I have, but that weird thing

where part of the tree also looks like a tree,

that's called self similarity.

It's like one of those triangles

with an infinite number of smaller triangles inside it

or whatever this thing is.

And unlike the self-similar shapes we see in nature,

these perfectly self-similar shapes are infinite.

We could zoom in or out

and continue to see those patterns repeat forever!

Mathematician Benoit Mandelbrot

named these self repeating shapes, fractals,

because they exist sort of in between dimensions

or in fractured dimensions.

What the heck does that mean?

Let's take a quick sidebar

to talk about how the way that mathematicians use a word,

it isn't always the same

as how you and I use a word.

(upbeat music)

You and I think of dimensions as the three that we live in

or the two that exist on paper

or even the one dimension of a line,

because that's what we learned in geometry class.

What Mandelbrot meant by, "Dimension,"

has to do with how different shapes fill space

as they get bigger or smaller

and this is kind of the key thing for us

as we explore fractals in nature.

You can 2X the length of this line

and you get twice as much line.

Another way of saying that is you scale it up

by two to the power of one.

If we do the same to a square,

2X its length and width, you get four times as much square,

or you scale it up by two to the two.

Do it to a cube, 2X length, width, and height

and we get eight times as much cube or two to the three.

This power right here

is the dimension Mandelbrot was talking about

and for simple shapes,

it matches with our usual idea of dimension.

But what's interesting about a fractal like this one

is when you scale it up by 2X,

you get three times as much fractal.

(fractal reverberating)

That exponent isn't one or two, you get 1.585 dimensions.

Even though the fractal sits in a two dimensional plane,

just like a regular triangle does,

when you scale it up, it doesn't fill space

quite the same as a two dimensional object.

The same thing is true for fractals with volume, like this.

To a mathematicianologist or whatever,

it's more than two dimensional,

but not quite three dimensional.

Fractals exist in this weird in-between space

and that's part

of what Mandelbrot found so fascinating about 'em.

By the way,

you know what Benoit B. Mandelbrot's middle name is?

Benoit B. Mandelbrot.

Nerdiest joke I know right there.

Anyway, Mandelbrot pointed out

that fractals are not just a toy

for mathematicians to make psychedelic art

for your dorm room wall.

They can help us understand nature better,

because they're everywhere.

To start off, why do trees even look like trees?

Well, the thing is, biologically speaking,

there's no such thing as a tree.

Sure, there are things you and I call, "Trees,"

because of the way they look.

(buoyant music)

But if you look at a tree like this one,

many of the plants we call, "Trees,"

are more closely related to things that aren't trees

and more distantly related to other things

that do look like trees.

So, "Tree," is just a way of describing plants

that look kind of tree-like.

It's almost as if growing fractal-like branches

that look similar at different scales

was the solution to some problem

that all these different plants faced

and that problem is soaking up a bunch of sun and CO2.

Growing tall is one solution to that problem

or maybe growing just a few gigantic leaves

on top of a trunk or even a canopy the size of a city block

with all the leaves on the very tip.

But all of these options require spending a bunch of energy

to grow for not that much gain,

basically, you gotta make a whole lot of wood

for not that much sun.

Luckily there's a better way to do it

and that's where being a fractal is really useful.

A perfect fractal lets you put infinite surface area

in a finite amount of space.

This snowflake isn't getting any bigger,

but you can keep zooming in

then you'll keep finding another smaller layer

just like the first.

And you can keep doing this forever,

meaning its outer edge,

the line you need to draw this shape,

is infinitely long.

Trees do something similar,

by growing out each level as a smaller version

of the previous level

a tree can pack a bunch of surface area in its volume,

not an infinite amount,

like a mathematically perfect fractal,

but it's a pretty cool way of soaking up more sun

without wasting energy by getting all bulky.

And it's no coincidence

that trees roots grow in a similar way,

they need lots of surface area

to soak up water and nutrients

and fractal branching is the best bang for their buck,

maximizing the volume that the tree can draw from

without wasting unneeded energy

building plumbing that's too big.

Meanwhile, inside our bodies, we have our own little trees.

A lung's job is to take in oxygen

and an adult body needs around 15 liters of O2 every hour.

If our lungs were just two balloons, they'd never keep up.

Fractal branching means our lungs can hold half the area

of a tennis court while staying packed up

nicely inside our chest.

(graphics whirring)

(crowd clapping)

And our lungs aren't the only trees we have inside us.

Our entire circulatory system

looks kind of like a bunch of fractal branches too.

We have almost a 100,000 kilometers of blood vessels

in our bodies delivering oxygen and nutrients

and removing wastes.

Fractal branching lets our circulatory system

pack in as many blood vessels as we need

to protect every point A with every point B,

while also spending the least possible energy

building our body's plumbing

and manufacturing all the blood that runs through it.

In a way, it's like each of these living systems has a goal.

A tree wants to soak up a bunch of light and CO2,

a lung wants to take in a bunch of air,

a blood vessel wants to exchange nutrients

with every cell in the body.

In all these cases,

fractal branches are the most efficient way

to scale up while staying basically the same size.

This secret pattern shows up in non-living things too.

All around the world, from their sources to their ends,

rivers arrange themselves into branching shapes.

And by now you can probably guess why,

at their source, fractal branching is the most efficient way

to drain water from a given area of land.

And at their mouths we see fractal branching

as sediment piles up and splits a river

into smaller and smaller strands.

Cracks and lightning bolts are both ways

of dissipating energy and it shouldn't surprise you

that fractal branches are the most efficient way to do that

inside of a given space.

And when scientists model all these ways of growing,

it turns out that, like perfect mathematical fractals,

these branching shapes are best described

as in between dimensions.

At this point, it might be tempting to think

there's one universal rule

that underlies every branching fractal pattern

that we see around us,

but as usual, nature isn't so predictable.

We also see fractal branches in crystals,

the shapes of snowflakes, even strange mineral deposits

people sometimes mistake for ancient plant fossils.

Similar fractals, but a different reason.

Here, things like temperature, humidity,

and the concentration of different chemicals

act as a set of rules for building the thing.

And as these structures grow,

those rules repeat themselves at multiple scales

giving us self-similar fractal shapes.

What's amazing is that as much

as these fractal shapes pop up in nature,

there isn't a single gene or law of physics or brain

making all these things grow fractal branches.

But one by one, as each of these systems evolved

to be as efficient as possible,

they all landed on the same solution

to their individual problems,

letting us look at things in an interestingly new dimension

and making them infinitely interesting.

Stay curious.

Hey guys, just jumping in here with a quick announcement.

Look, it's an undisputed fact that everything looks cooler

when you film it with a drone, right?

I don't make the rules, it's just how it is.

And I think there are some stories

that, well, you can only tell

from that perspective, the overview perspective.

Which is why I have a whole other show called, "Overview,"

about stories just like that.

And we are back with new videos,

it's over on the PBS Terra channel.

You're gonna love this,

We've won like real life science journalism awards

for the stuff we make over there.

It's really cool.

Go check it out, there's a link down the description

or you can click, you know, up there,

wherever it's gonna be and I'll see you on, "Overview."

Now, back to your regularly scheduled end-card.

You know what else is infinitely complex and interesting?

All of you lovely people who support the show on Patreon.

Thank you, every one of you.

You are the reason that we can research questions like this

and bring you interesting answers,

like the one that you just filled your brain with.

If you would like to join our community,

directly support this show, help us make videos like this,

and also find out about new videos before anybody else,

and a whole bunch of other cool stuff,

there's a link down to the description

where you can learn more.

See you in the next video.

By the way,

you know what Benoit B. Mandelbrot's middle name is?

"Ben Watt," did I just call him, "Ben Watt?"

- [Crew Member] Yeah!

That's not how we say that...

Ben-oit!