LIMITE: a Ideia Fundamental do Cálculo
Summary
TLDRDaniel Nunes takes us on a journey to understand the concept of limits, a fundamental idea in calculus. He explains limits intuitively, using the example of estimating the square root of 2, and then delves into the formal definition involving epsilon and delta. The video clarifies the misconceptions around limits and emphasizes their importance in defining exponential functions and the calculus operations of derivatives and integrals. Nunes encourages a blend of intuitive thinking with rigorous mathematical understanding to appreciate the depth of limits in mathematics.
Takeaways
- 😀 Calculus is one of the greatest creations in the history of mathematics, and it relies fundamentally on the concept of limits.
- 📚 The script introduces the concept of limits as a crucial idea in calculus, which is often the first contact with higher mathematics.
- 🕰 Historically, calculus was taught in secondary education but has since been phased out, which is seen as a loss due to the reduced exposure to important mathematical ideas.
- 🌟 The intuitive notions of continuous change, such as continuous heating and motion, have challenged brilliant minds for millennia, leading to the development of calculus in the 17th century.
- 👨🔬 Isaac Newton is credited with the independent creation of calculus, though it was built upon the intuitive concept of limits without formal rigor.
- 🔢 The script uses the example of estimating the square root of 2 to illustrate the concept of limits and approximations, highlighting the connection between limits and real numbers.
- 📉 The importance of functions in modern science is discussed, with functions being a natural way to describe relationships, such as the position of a particle as a function of time.
- 📈 The concept of limits is explored in the context of functions, explaining how the behavior of a function can be understood as it approaches a certain value.
- 🚫 The script clarifies that the limit is not about the function's value at a specific point but rather its behavior as it approaches that point without actually reaching it.
- 📚 The formal definition of a limit using the Greek letters epsilon (ε) and delta (Δ) is introduced, emphasizing the rigorous mathematical approach to understanding limits.
- 📐 The geometric interpretation of epsilon and delta is provided to help visualize the concept of limits, showing how any level of error can be accommodated with an appropriate distance Delta.
- 🔑 The script mentions that the concept of limits is essential for understanding exponential functions and is integral to the definitions of derivatives and integrals in calculus.
Q & A
What is the main topic of the video?
-The video discusses the concept of limits in mathematics, particularly in the context of calculus, and how it is fundamental to understanding continuous change.
Why is calculus considered one of the greatest creations in the history of mathematics?
-Calculus is considered one of the greatest creations because it provides a framework for understanding continuous change, which is essential in many fields of science and mathematics. It relies on the concept of limits, which is crucial for defining derivatives and integrals.
What historical context is provided about the teaching of calculus?
-The video mentions that there was a time when the basics of calculus were taught in high school, but with the increasing specialization in curricula, this is no longer the case. This change has reduced people's exposure to some of the most important ideas in the history of mathematics.
How did ancient mathematicians approach the idea of continuous change?
-Ancient mathematicians had intuitive notions of continuous change, such as continuous heating or movement, but it wasn't until the 17th century, with the rise of modern science, that a more formal understanding of continuous variation developed alongside calculus.
What role did Isaac Newton play in the development of calculus and the concept of limits?
-Isaac Newton is one of the independent creators of calculus. He treated the concept of limits intuitively, without a formalized approach. His work laid the foundation for the development of calculus, even though the rigorous definition of limits came about 200 years later.
What is the significance of the square root of 2 in the context of limits?
-The square root of 2 is used as an example to illustrate the idea of limits. The video explains how this number, while well-defined, can only be approximated on the real number line, demonstrating the deep connection between limits and the structure of real numbers.
How do limits relate to functions in mathematics?
-Limits are closely related to functions. They describe the behavior of a function as the input approaches a certain value. This concept is central to understanding continuous functions and the behavior of functions near specific points.
What is an intuitive understanding of a limit as described in the video?
-An intuitive understanding of a limit involves imagining what value a function would approach as its input gets closer and closer to a specific point, without actually reaching that point. This approach helps to grasp the idea of a function's behavior near a given value.
What is the formal definition of a limit using epsilon and delta, and why is it important?
-The formal definition of a limit states that for any arbitrarily small error margin (epsilon), there exists a small distance (delta) such that if the input of the function is within this distance of a certain point (but not equal to it), the function's output will be within the error margin of the limit value. This definition is important because it provides a rigorous framework for understanding limits and avoids incorrect conclusions based on intuition alone.
How does the video explain the concept of limits in higher dimensions?
-The video explains that in higher dimensions, the concept of a limit can be visualized similarly to the one-dimensional case. For example, in two dimensions, the limit is defined in terms of a disk of arbitrary radius (epsilon) around a point, with a corresponding smaller disk (delta) that ensures all points within this smaller disk are mapped within the larger disk by the function.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Calculus - Introduction to Calculus

Limit of a Function using a Graph - Basic/Differential Calculus

Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)
Universo Mecánico 07 Integración
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
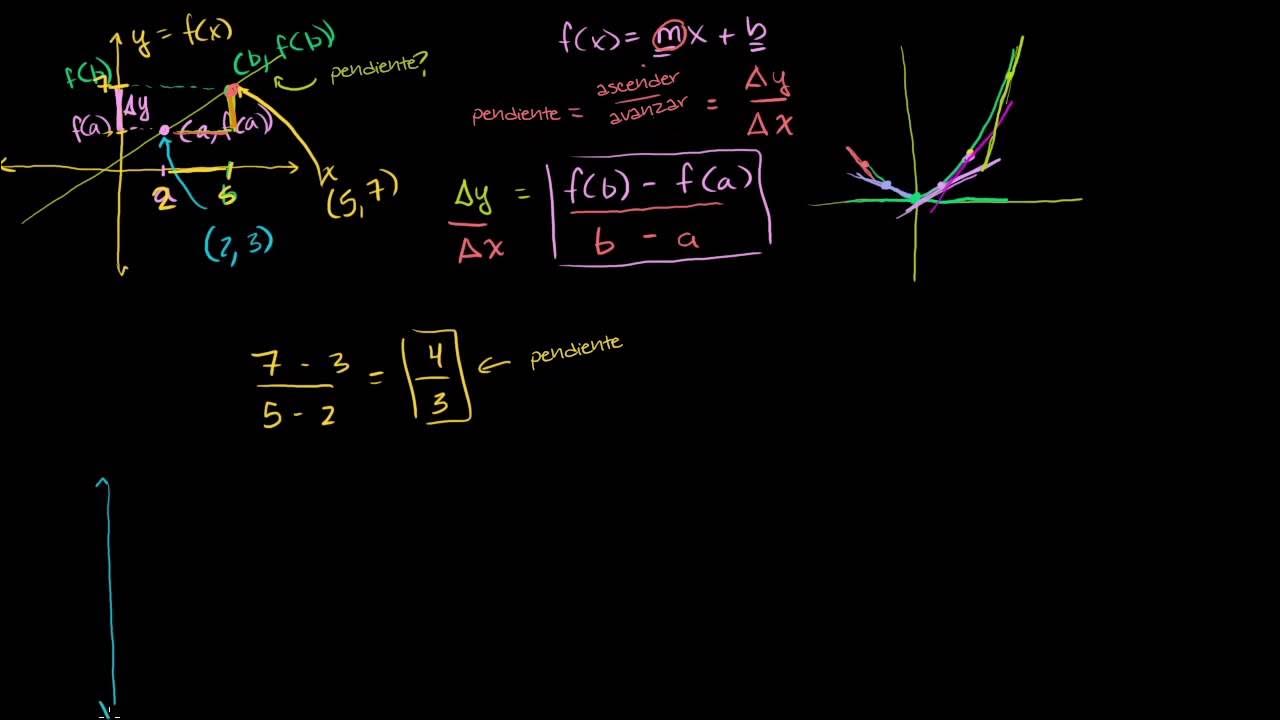
Cálculo: Derivadas 1 (nueva versión HD)
5.0 / 5 (0 votes)