Cálculo: Derivadas 1 (nueva versión HD)

Summary

This video script introduces the concept of slope, first revisiting basic algebra before transitioning into calculus. The script starts with defining the slope of a line using two points and their coordinates, explaining how to calculate it through differences in x and y values. The script then extends the concept to curves, demonstrating how the slope varies at different points on a curve. It introduces the idea of a tangent line and the derivative, explaining how limits help find the exact slope at any given point, thus laying the foundation for understanding derivatives in calculus.

Takeaways

• 😀 The concept of slope is typically introduced in early algebra courses, where we learn how to calculate the slope of a line.
• 😀 The slope of a line is defined as the change in y (vertical change) divided by the change in x (horizontal change) between two points.
• 😀 A line has a constant slope, whereas in a curve, the slope changes at each point along the curve.
• 😀 To calculate the slope of a line, select two points on the line and apply the formula: slope = (change in y) / (change in x).
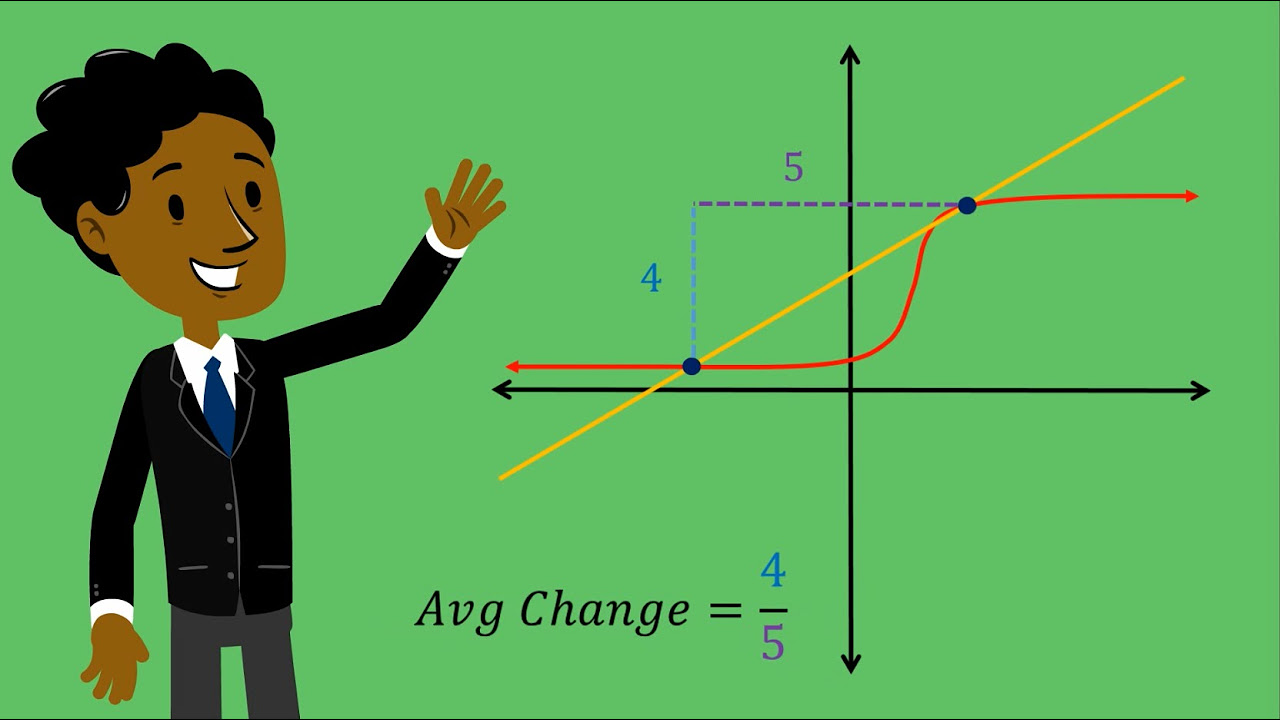
• 😀 For example, for the points (2, 3) and (5, 7), the slope would be calculated as (7 - 3) / (5 - 2) = 4 / 3.
• 😀 In curves, the slope at a specific point can vary, and this requires a more advanced concept to calculate.
• 😀 For a curve, we need two points close to each other to calculate the slope, leading us to define a secant line between these points.
• 😀 The formula for the slope of a secant line is similar to the line's slope calculation, but with two points on the curve.
• 😀 To find the exact slope at a single point on the curve, we take the limit of the slope of the secant line as the second point gets infinitely close to the first.
• 😀 The process of finding the limit as the points get closer gives us the derivative of the function, representing the instantaneous slope of the curve at a specific point.
• 😀 The derivative, denoted as f'(x), provides the slope of the tangent line to the curve at any given point, and is a crucial concept in calculus.

Q & A

What is the basic formula for calculating the slope of a line?

The slope of a line is calculated by the formula: (change in y) / (change in x), which is written as (F(b) - F(a)) / (b - a) when using two points on the line.

How do we calculate the slope of a line when given two points on the line?

To calculate the slope between two points, we subtract the y-coordinate of the first point from the y-coordinate of the second point (change in y), and subtract the x-coordinate of the first point from the x-coordinate of the second point (change in x). Then, divide the change in y by the change in x.

What happens to the slope when the points on the line are closer together?

As the points on the line get closer together, the slope remains constant for a straight line. This means that regardless of where you measure, the slope of a straight line is always the same.

How is the concept of slope different when applied to a curve?

Unlike a straight line where the slope is constant, the slope of a curve changes at every point along the curve. To find the slope at a specific point on the curve, we need to look at the slope of the tangent line at that point.

What is the slope of a tangent line at a specific point on a curve?

The slope of a tangent line at a point on a curve represents the rate of change of the function at that point. It is calculated as the derivative of the function at that specific point.

What is a secant line, and how is it used to find the slope of a curve?

A secant line is a line that intersects the curve at two distinct points. By calculating the slope of the secant line between two points, we approximate the slope of the curve. As the two points get closer, the slope of the secant line approaches the slope of the tangent line.

What role does the concept of a limit play in calculating the slope of a curve?

The concept of a limit is crucial because it allows us to find the slope of the tangent line by considering the slope of the secant line as the two points approach each other. As the distance between the two points (h) tends to zero, the slope of the secant line converges to the slope of the tangent line, which is the derivative.

How is the derivative of a function related to the slope of a curve?

The derivative of a function represents the slope of the tangent line at any point on the curve. It is the limit of the slope of the secant line as the two points used to calculate the secant line become infinitesimally close to each other.

What is the formula for the slope of a secant line when given two points on the curve?

The formula for the slope of the secant line is: (f(x0 + h) - f(x0)) / h, where x0 is the first point, x0 + h is the second point, and h is the horizontal distance between the two points.

How do we calculate the slope of the tangent line at a point on a curve using limits?

To calculate the slope of the tangent line at a point on a curve, we take the limit of the slope of the secant line as h approaches zero. The formula becomes: lim (h → 0) [(f(x0 + h) - f(x0)) / h]. This gives the derivative of the function, which is the slope of the tangent line at the point.