Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)
Summary
TLDRThis video introduces a comprehensive calculus course, starting with the fundamental concept of limits. Using relatable examples like the expansion of a heated metal plate, the instructor explains how limits describe the behavior of a function as a variable approaches a certain value. The video also covers symbolic notation, graphing limits, and provides step-by-step examples, including limits of linear and rational functions. The content is designed to help students build a solid understanding of limits, laying the groundwork for more advanced calculus topics in various scientific and engineering fields.
Please replace the link and try again.
Q & A
What is the concept of a limit in calculus?
-A limit in calculus describes the behavior of a function as the input (x) approaches a specific value, without necessarily reaching it. It focuses on how the function behaves near a certain point, rather than exactly at that point.
How is the concept of a limit applied to a metal plate in the video?
-In the video, a metal plate is used to demonstrate limits. As the plate is heated, its side length (x) approaches 3 cm. As x approaches 3, the area of the plate approaches 9 cm². This illustrates how the function's behavior near a specific point (x = 3) leads to a limit.
What happens when x approaches 3 for the function f(x) = x²?
-When x approaches 3 for the function f(x) = x², the area (f(x)) approaches 9. In limit notation, we write this as lim(x → 3) x² = 9, meaning the value of the function approaches 9 as x gets closer to 3.
What does the notation lim(x → 3) x² = 9 represent?
-The notation lim(x → 3) x² = 9 indicates that as x approaches 3, the value of the function x² approaches 9. It is a formal way to express that the limit of x² as x tends to 3 is 9.
What is the importance of limits when x is close but not equal to a specific value?
-The importance of limits lies in determining the behavior of a function as x approaches a specific value. In many cases, we don't care about the function's value exactly at that point, but rather how the function behaves as it gets closer to that point.
What is the outcome when the function f(x) = 2x - 1 is evaluated as x approaches 3?
-As x approaches 3, the function f(x) = 2x - 1 approaches 5. In limit notation, we write this as lim(x → 3) (2x - 1) = 5.
What does it mean when a function gives an indeterminate form like 0/0?
-An indeterminate form like 0/0 occurs when direct substitution of a value into a function results in a division by zero. This indicates that further analysis is required to determine the limit, as simple substitution doesn't give a clear result.
What is the limit of the function f(x) = (x² - 1) / (x - 1) as x approaches 1?
-The function f(x) = (x² - 1) / (x - 1) gives an indeterminate form 0/0 when x = 1. However, by factoring and simplifying the expression, we can determine that the limit as x approaches 1 is 2. In limit notation: lim(x → 1) (x² - 1) / (x - 1) = 2.
Why can't we directly substitute x = 1 in the function f(x) = (x² - 1) / (x - 1)?
-Direct substitution of x = 1 into the function f(x) = (x² - 1) / (x - 1) results in 0/0, which is an indeterminate form. This means we can't determine the limit directly by substitution, and we need to analyze the function's behavior as x approaches 1.
How do the left-hand and right-hand limits differ when evaluating a function?
-The left-hand limit (denoted as x → a⁻) refers to the behavior of a function as x approaches a value from the left (with x < a), while the right-hand limit (denoted as x → a⁺) refers to the behavior as x approaches from the right (with x > a). If the left-hand and right-hand limits are not the same, the limit does not exist.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Limit of a Function using a Graph - Basic/Differential Calculus

Eps.8 KALKULUS 1: Limit - Pendahuluan Limit

Give Me 20 minutes, and Calculus Will Finally Make Sense.
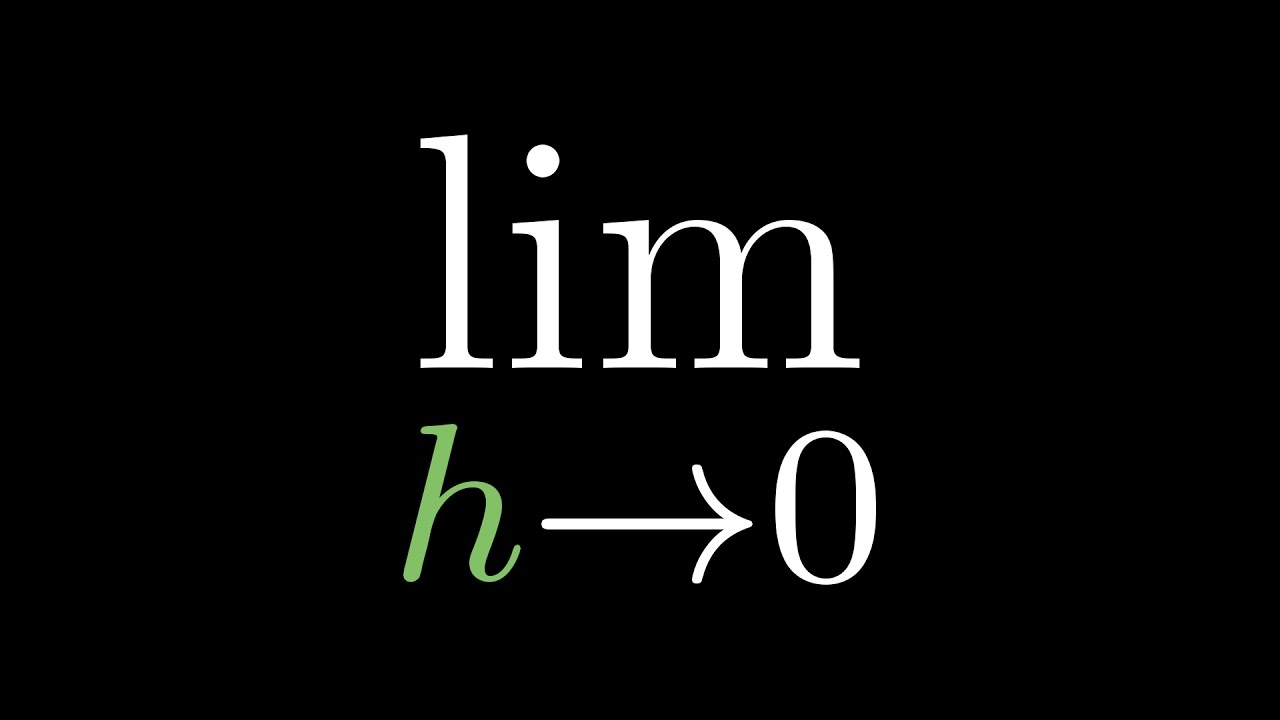
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

Calculus - Introduction to Calculus

Límite de una función real
5.0 / 5 (0 votes)