RÁPIDO e FÁCIL | SEMELHANÇA DE TRIÂNGULOS
Summary
TLDRThis video provides a comprehensive guide to triangle similarity in geometry, explaining key concepts such as the conditions for similarity, proportionality of corresponding sides, and how to use cross-multiplication to solve for unknown values. Through clear examples, the video demonstrates how to apply these principles in real-world scenarios, including calculating missing side lengths, heights, and areas using triangle proportions. Viewers will learn how to confidently tackle problems related to similar triangles and use these techniques effectively in their studies and exams.
Takeaways
- 😀 Similar triangles have equal corresponding angles and proportional sides.
- 😀 The ratio of corresponding sides in similar triangles remains constant.
- 😀 When calculating proportional sides, use corresponding angles and sides as the basis for the ratio.
- 😀 The ratio of similarity can be applied to calculate missing side lengths using cross-multiplication.
- 😀 Problems involving shadows or heights can be solved using the properties of similar triangles.
- 😀 The key to solving triangle similarity problems is recognizing corresponding angles and setting up correct proportions.
- 😀 The perimeter of similar triangles is also proportional, meaning the perimeter of the smaller triangle is a fraction of the larger triangle's perimeter.
- 😀 The principle of similarity can be applied to a variety of real-world situations, such as calculating shadows cast by objects.
- 😀 For shadow-related problems, the height of an object and its shadow can form similar triangles, allowing for the calculation of missing dimensions.
- 😀 Always double-check the proportions to ensure they are based on the correct corresponding sides to avoid errors in calculations.
Q & A
What is the main topic of the video script?
-The main topic of the video is the concept of triangle similarity, specifically how to calculate the proportional ratios between corresponding sides and angles of similar triangles.
What is the first key concept introduced in the video?
-The first key concept introduced is the similarity of triangles, which is determined by the equality of their angles. This allows the establishment of proportionality between corresponding sides.
How can we identify if two triangles are similar?
-Two triangles are similar if they have the same corresponding angles, and the sides of one triangle are proportional to the sides of the other triangle.
What does 'homologous sides' refer to in the context of triangle similarity?
-Homologous sides refer to the sides of two similar triangles that are opposite corresponding equal angles. The ratio of these homologous sides gives the similarity ratio.
How can we calculate the similarity ratio between two similar triangles?
-The similarity ratio can be calculated by comparing the lengths of corresponding sides or other related elements, such as heights, perimeters, or altitudes of the triangles.
What is the formula for the similarity ratio based on side lengths?
-The formula for the similarity ratio based on side lengths is: (side of the smaller triangle) / (corresponding side of the larger triangle). This ratio must be consistent across all corresponding sides.
In the example with the shadow of a post, how is the shadow length calculated?
-The shadow length is calculated by applying the similarity of triangles. The corresponding sides of the smaller triangle (formed by the height of the post and the shadow) and the larger triangle (formed by the light source and its shadow) are proportional.
What does the expression 'MN parallel ABC' mean in the script?
-'MN parallel ABC' indicates that the line MN is parallel to the line ABC, which ensures that the corresponding angles between the two triangles are equal, making them similar.
What is the importance of having a common angle between two similar triangles?
-Having a common angle between two similar triangles ensures that both triangles share one angle, which is crucial for proving their similarity. This angle helps establish proportionality between their corresponding sides.
Why is the height ratio important in the context of similar triangles?
-The height ratio is important because it follows the same proportionality rule as the sides and can be used to calculate other unknowns, such as the height of a triangle or the length of a shadow.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Semelhança de Triângulos - Professora Angela
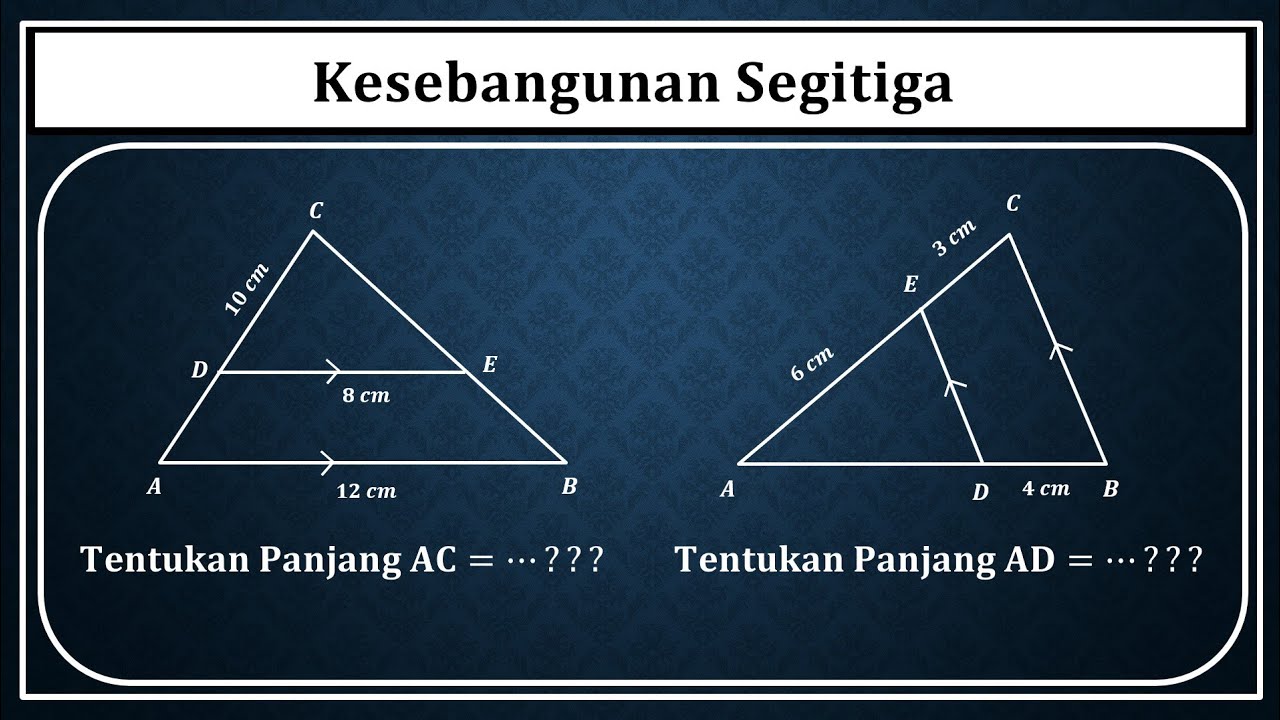
Kesebangunan segitiga
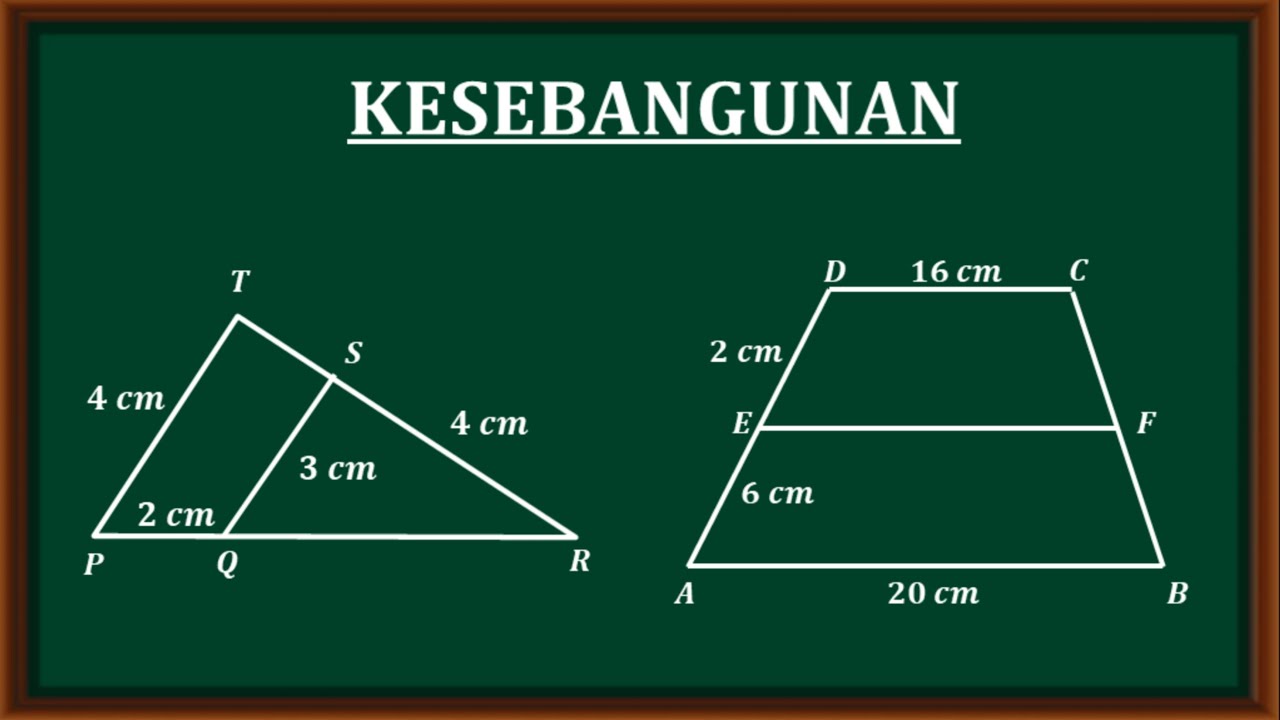
Kesebangunan - soal dan pembahasan materi kesebangunan matematika tingkat SMP kelas ix

Kurikulum Merdeka Materi Matematika Kelas 7 Bab 5 Kesebangunan

Kesebangunan Pada Segitiga. Part 2, Rumus-rumus

Kesebangunan Segitiga: Kesebangunan Segitiga Siku-siku (Belajar Matematika Kelas 7) - Kak Hasan
5.0 / 5 (0 votes)