Semelhança de Triângulos - Professora Angela

Summary

This video explains the concept of triangle similarity, focusing on conditions such as congruent corresponding angles and proportional sides. It covers how to recognize similar triangles and how to use proportions to solve for unknown values in practical examples. The video also discusses the fundamental theorem of similarity, applying it to real-world problems with clear, step-by-step demonstrations. Viewers will learn about the different types of triangle similarity cases—angle-angle, side-angle-side, and side-side-side—and how to apply these concepts for accurate solutions.

Takeaways

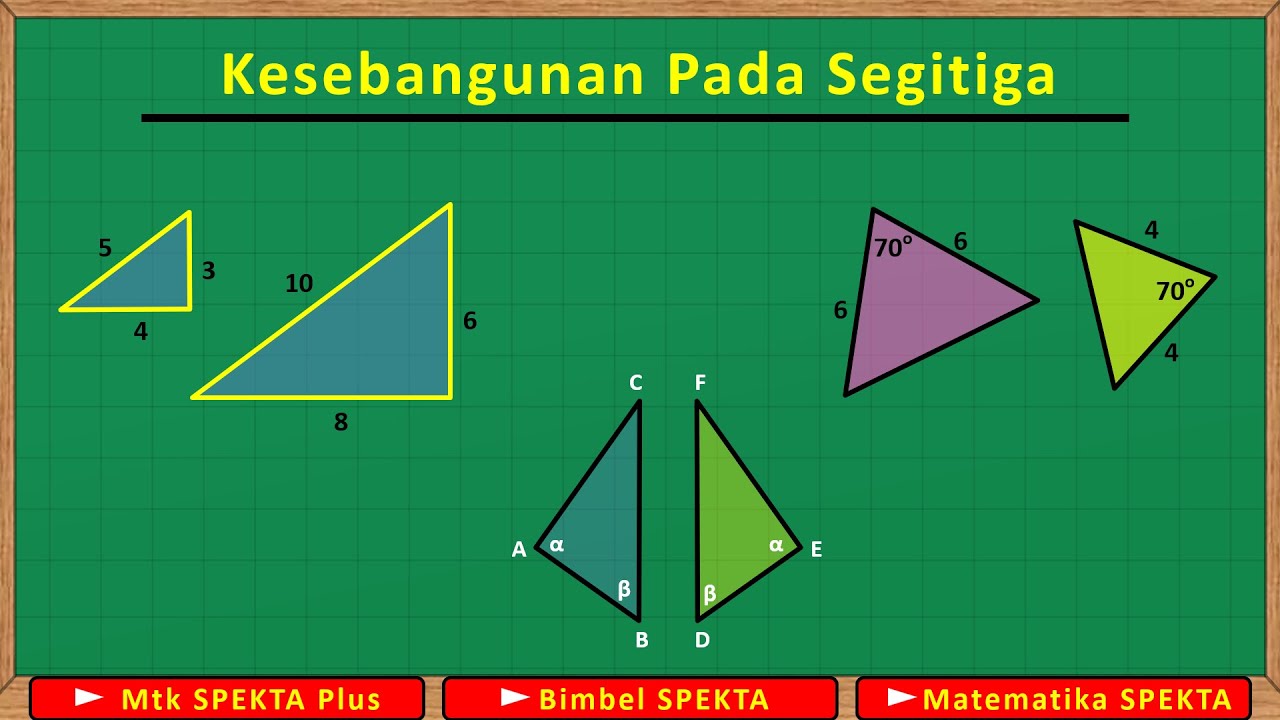
• 😀 Two triangles are similar if their corresponding angles are congruent and their corresponding sides are proportional.
• 😀 The Angle-Angle (AA) criterion states that two triangles are similar if two corresponding angles are equal.
• 😀 The Side-Angle-Side (SAS) criterion states that if two sides are proportional and the included angle is the same, the triangles are similar.
• 😀 The Side-Side-Side (SSS) criterion states that if all three sides of two triangles are proportional, the triangles are similar.
• 😀 Corresponding sides of similar triangles are proportional, allowing for the setup of ratios to solve for unknown values.
• 😀 The constant of proportionality (also known as the similarity ratio) indicates how much one triangle is a scaled version of the other.
• 😀 Using proportions and the rule of three, unknown values like side lengths can be calculated in similar triangles.
• 😀 The principle of parallel lines is used to create smaller similar triangles by drawing a line parallel to one side of the triangle.
• 😀 The sum of the interior angles of any triangle is always 180°, which helps in determining unknown angles in similar triangles.
• 😀 When working with similar triangles, it's essential to ensure that corresponding sides and angles are matched properly for accurate calculations.

Q & A

What are the two conditions for triangles to be similar?

Two triangles are similar when their corresponding angles are congruent and their corresponding sides are proportional.

How can we express the proportionality of corresponding sides in similar triangles?

The proportionality of corresponding sides is expressed as a ratio, and a proportion can be formed by comparing the corresponding sides of two similar triangles.

What is the constant of proportionality in similar triangles?

The constant of proportionality, also known as the ratio of similarity, indicates how much one triangle has been scaled relative to the other. It tells us how many times larger or smaller one triangle is compared to the other.

How do we solve for missing side lengths in similar triangles?

To solve for missing side lengths, we set up a proportion using the known corresponding side lengths from both triangles. Then, we use cross-multiplication to solve for the unknown value.

What is the method for solving for 'x' and 'y' in similar triangles?

To solve for 'x' and 'y', we first set up a proportion for the corresponding sides of the two triangles. We then apply the cross-multiplication method or the rule of three to solve for the unknown variables.

How does the concept of similar triangles apply when a line is drawn parallel to one side of a triangle?

When a line is drawn parallel to one side of a triangle, it creates two smaller triangles within the original triangle that are similar to each other. This is known as the fundamental property of similar triangles.

What is the sum of the interior angles in any triangle?

The sum of the interior angles in any triangle is always 180 degrees.

How can we calculate the missing angles of a triangle using the sum of its angles?

To calculate the missing angles of a triangle, we add up the known angles and subtract the sum from 180 degrees. The remaining angle is the missing one.

What is the importance of using proportions when solving problems with similar triangles?

Using proportions helps to maintain the relationship between corresponding sides of similar triangles. By setting up a proportion, we can solve for unknown side lengths efficiently and accurately.

Can the rule of three be applied to any type of proportional relationship?

Yes, the rule of three can be applied to any proportional relationship where three values are known, and the fourth value needs to be calculated. It is especially useful in problems involving similar triangles.