Kesebangunan Pada Segitiga. Part 2, Rumus-rumus

Summary

In this video, the concept of similarity in triangles is explored, focusing on proving the similarity of two triangles through corresponding angles and proportional sides. The presenter demonstrates how two triangles, created by drawing a parallel line within a triangle, show equal corresponding angles and proportional sides. The video further explains how to derive formulas using variables to express the relationships between the corresponding sides. Key formulas for solving triangle similarity problems are introduced, providing valuable tools for geometric calculations. This serves as an essential guide for understanding and applying triangle similarity principles.

Takeaways

• 😀 The video covers the concept of similarity in triangles, specifically focusing on the properties and formulas related to similar triangles.
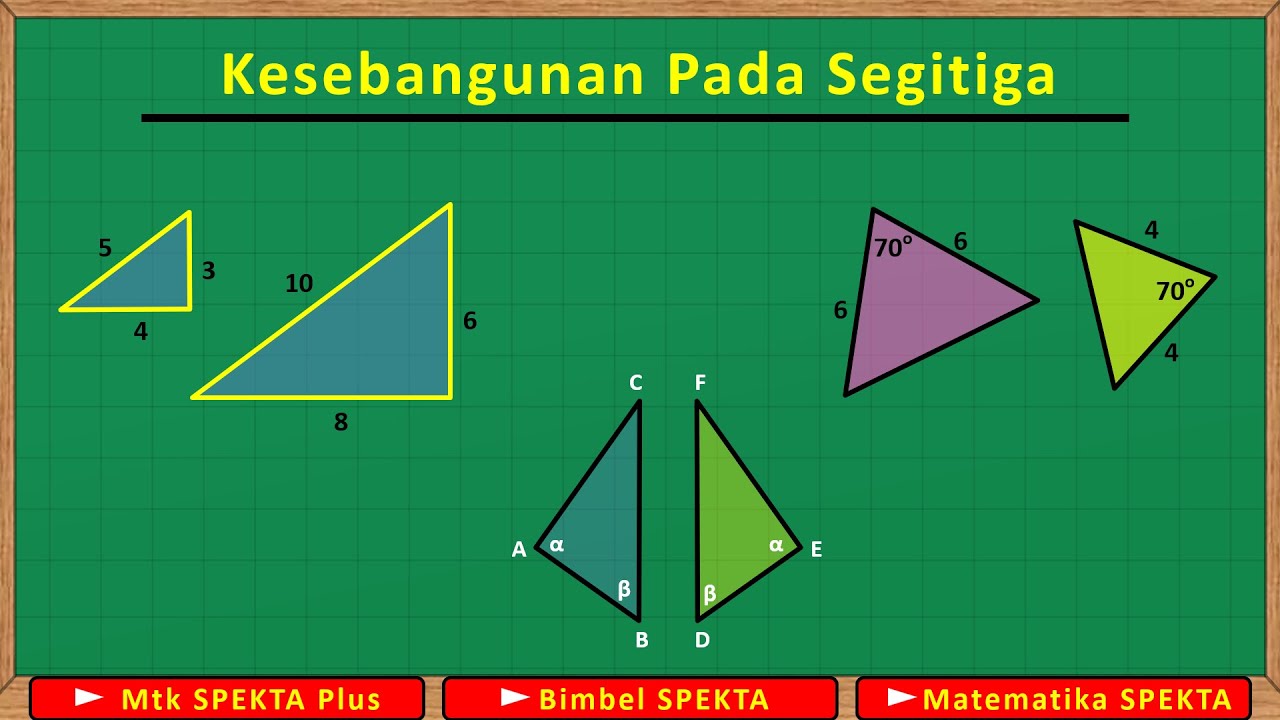
• 😀 Two triangles are considered similar if two pairs of corresponding angles are equal in measure.
• 😀 In the example, triangle ABC and triangle DEC are shown to be similar because angles A and D, B and E, and C and C are congruent.
• 😀 When two triangles are similar, the ratios of the lengths of their corresponding sides are proportional.
• 😀 The parallel line DE inside triangle ABC is key to establishing the similarity between the two triangles.
• 😀 The corresponding sides of similar triangles, such as AC and DC, BC and EC, AB and DE, maintain a constant ratio.
• 😀 The formula for the proportionality of corresponding sides is expressed as: CD/CA = CE/CB = DE/AB.
• 😀 Variables such as P, R, A, B, Q, and S are introduced to represent the lengths of the sides of the triangles.
• 😀 Using these variables, the relationship between the corresponding sides can be written as: P/(P + R) = Q/(Q + S) = A/B.
• 😀 Algebraic manipulation of these proportions leads to important formulas, such as PR = QR and P/Q = R/S, which are used to solve problems involving similar triangles.
• 😀 The lesson concludes by indicating that more examples and calculations related to triangle similarity will be covered in part 3 of the series.

Q & A

What is the main topic of the video?

The main topic of the video is the concept of triangle similarity, specifically focusing on the conditions that define similarity and the proportionality of corresponding sides.

How do we identify two triangles as similar?

Two triangles are considered similar if two pairs of corresponding angles are equal and the ratios of their corresponding sides are proportional.

What are the corresponding angles in the two triangles discussed?

The corresponding angles are: Angle A in triangle ABC corresponds to Angle D in triangle DEC, Angle B corresponds to Angle E, and Angle C corresponds to Angle C.

Why are the triangles ABC and DEC similar?

The triangles ABC and DEC are similar because line DE is parallel to line AB, and the angles A, B, and C correspond to angles D, E, and C respectively. The parallel lines ensure that the angles are equal due to geometric properties.

What is the proportionality rule for the sides of similar triangles?

For two similar triangles, the ratios of corresponding sides are equal. Specifically, for triangles ABC and DEC: AC/DC = CB/CE = AB/DE.

How can we express the proportionality of the sides using variables?

Using variables, the proportionality of the sides can be expressed as: CD/CA = CE/CB = DE/AB.

What happens when we substitute the side lengths into the proportionality equation?

When substituting the side lengths into the proportionality equation, we get expressions like: P/(P+R) = Q/(Q+S) = A/B, where the variables represent the lengths of the sides.

What is the significance of the algebraic manipulation shown in the video?

The algebraic manipulation simplifies the proportional relationships into equations like PR = QS and P/Q = R/S, which can be used to calculate unknown side lengths in similar triangles.

What is the formula derived from the proportionality of the sides?

The formula derived from the proportionality of the sides is: CD/CA = CE/CB = DE/AB, which is the fundamental rule for similar triangles.

What does the teacher suggest for further learning about this topic?

The teacher suggests watching part 3 of the video for practical examples and further explanations on how to apply the concepts of triangle similarity in calculations.