Kurikulum Merdeka Materi Matematika Kelas 7 Bab 5 Kesebangunan

Summary

In this educational video, the topic of mathematical similarity is explored, focusing on angles and triangles. Key concepts include complementary angles, straight angles, vertically opposite angles, and angles on parallel lines. The video covers practical problem-solving techniques, such as calculating unknown angles using simple subtraction. It also introduces the concept of similarity in geometry, explaining how the sizes of corresponding sides in similar triangles are proportional. The video provides step-by-step solutions and tips to solve geometry problems related to these concepts, making it accessible and engaging for 7th-grade students.

Takeaways

• 😀 Sudut berpenyiku always forms a 90° angle, like the L-shaped corner, and when the sum of two angles is 90°, you can easily find the missing angle by subtracting from 90°.
• 😀 Sudut berpelurus always forms a 180° angle, and if two angles are supplementary, you can subtract the known angle from 180° to find the missing angle.
• 😀 Opposite angles (sudut bertolak belakang) are always equal. For example, if one angle is 90°, the opposite will also be 90°.
• 😀 When two lines are parallel, corresponding angles are equal. Sudut pada dua garis sejajar has matching angles on opposite sides of the transversal.
• 😀 The principle of kesebangunan (similarity) involves two shapes that have corresponding angles and proportional sides, like zooming in or out with a camera.
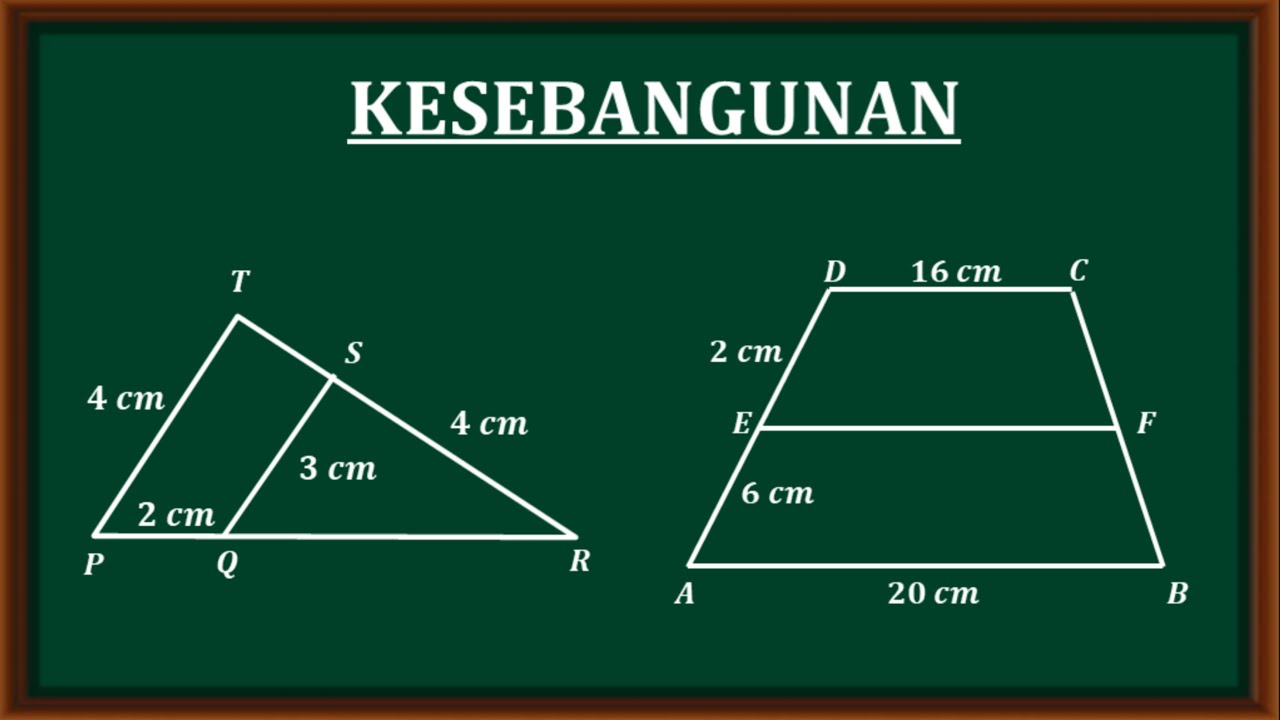
• 😀 Kesebangunan on triangles means that corresponding angles are equal, and corresponding sides have proportional lengths. This relationship allows comparison between different-sized triangles.
• 😀 The ratio of corresponding sides in similar triangles can help calculate missing side lengths by maintaining consistent ratios, such as AB/DE = BC/EF.
• 😀 In a practical example, if you have the lengths of sides in similar triangles, you can use the proportionality to find unknown values by setting up ratios.
• 😀 When solving for missing sides in similar triangles, always simplify the ratios and perform cross-multiplication to find the unknown values.
• 😀 Understanding the basics of angles and similarity is essential for solving problems in geometry, especially when dealing with parallel lines and triangles.

Q & A

What is the sum of two complementary angles?

Two complementary angles always add up to 90 degrees, as demonstrated when angle R (50 degrees) and angle S (40 degrees) form a right angle.

How do you calculate the missing angle in a straight line?

To calculate the missing angle on a straight line, subtract the known angle from 180 degrees. For example, if angle U is 120 degrees, angle T is 60 degrees, as 180 - 120 = 60.

What is the relationship between vertically opposite angles?

Vertically opposite angles are always equal. For instance, angle 1 equals angle 3, and angle 2 equals angle 4, regardless of the angle size.

What are parallel lines, and what is their significance in angle relationships?

Parallel lines are lines that run in the same direction and never intersect. Angles formed by a transversal cutting through parallel lines follow specific rules, such as corresponding angles being equal.

How can you find the measure of an unknown angle when two angles are supplementary?

When two angles are supplementary (adding up to 180 degrees), subtract the known angle from 180 degrees to find the unknown angle. For example, if angle A is 45 degrees, then angle B is 135 degrees because 180 - 45 = 135.

What does similarity mean in geometry?

Similarity in geometry refers to two figures that have the same shape but may differ in size. The corresponding angles are equal, and the sides have proportional lengths.

How do you verify that two triangles are similar?

To verify two triangles are similar, check that their corresponding angles are equal and the lengths of corresponding sides are proportional.

What is the rule for corresponding angles in parallel lines?

When a transversal cuts through two parallel lines, the corresponding angles formed are equal. For example, angle 1 equals angle A, angle 2 equals angle B, and so on.

What is the relationship between the sides of two similar triangles?

In similar triangles, the corresponding sides are proportional. For example, if one triangle has sides of length 8, 6, and 10, and the other has sides of length 4, 3, and 5, the ratio of the corresponding sides is 2:1.

How do you solve for an unknown side in a similar triangle problem?

To solve for an unknown side in similar triangles, set up a proportion using the corresponding sides of the two triangles. Cross-multiply and solve for the unknown side. For example, if the sides of two triangles are in the ratio 2:1, you can use this ratio to find the unknown side by solving the proportion.