Gráfica Función Lineal con Pendiente y Ordenada al Origen
Summary
TLDREn este video, Riccardo explica cómo graficar funciones lineales utilizando la pendiente y la ordenada al origen. Comienza describiendo cómo identificar y usar la pendiente, ya sea positiva o negativa, y cómo la ordenada al origen es el punto donde la gráfica corta el eje vertical. A través de ejemplos prácticos, muestra cómo moverse en el plano cartesiano para trazar la línea correctamente. La pendiente positiva genera una recta creciente, mientras que la pendiente negativa una recta decreciente. Al final, enfatiza cómo la gráfica de una función lineal depende de estas dos constantes y cómo interpretarlas fácilmente.
Takeaways
- 😀 La función lineal tiene dos constantes clave: la pendiente y la ordenada al origen.
- 😀 La pendiente es el valor que multiplica a 'x' y determina la inclinación de la recta.
- 😀 La ordenada al origen es el punto donde la función corta el eje vertical de las y.
- 😀 La pendiente puede ser positiva o negativa, lo que afecta si la recta es creciente o decreciente.
- 😀 Si la pendiente es negativa, como en el caso de -3, se debe mover una unidad a la derecha y luego bajar tres unidades.
- 😀 Si la pendiente es positiva, como en el caso de 2/3, se mueve tres unidades a la derecha y luego se sube dos unidades.
- 😀 Para graficar una función lineal, primero se marca el punto de la ordenada al origen en el eje y.
- 😀 Una vez marcado el punto de partida, se utiliza la pendiente para determinar los siguientes puntos a trazar en la gráfica.
- 😀 Con dos puntos ya marcados en la gráfica, se traza una línea recta que representa la función lineal.
- 😀 La pendiente de la recta indica cuán rápido la función sube o baja por cada unidad de x.
- 😀 Al graficar funciones lineales, es importante recordar que la pendiente positiva muestra una recta creciente y la negativa una decreciente.
Q & A
¿Qué es la pendiente en una función lineal?
-La pendiente es el valor que determina la inclinación de la recta en la gráfica de la función lineal. Se reconoce porque es el número que multiplica a la variable 'x'. Si la pendiente es positiva, la recta será creciente, y si es negativa, la recta será decreciente.
¿Qué es la ordenada al origen en una función lineal?
-La ordenada al origen es el valor donde la recta corta al eje vertical de las 'y'. Es el valor de la función cuando 'x' es igual a 0. En la fórmula de la función lineal, es el término independiente.
¿Cómo se identifica el punto de partida de la gráfica de una función lineal?
-El punto de partida se identifica a partir de la ordenada al origen, que es el valor de 'y' cuando 'x' es igual a 0. Este es el primer punto que se marca en la gráfica.
¿Cómo se grafica una función lineal con pendiente negativa?
-Para graficar una función con pendiente negativa, primero se marca la ordenada al origen en el eje 'y'. Luego, desde ese punto, se mueve una unidad hacia la derecha y se baja tantas unidades como lo indique la pendiente negativa.
Si la pendiente es -3, ¿cómo se mueve en la gráfica?
-Si la pendiente es -3, te mueves una unidad hacia la derecha y luego bajas 3 unidades, ya que la pendiente negativa indica que la recta desciende.
¿Cómo se grafica una función con pendiente positiva?
-Para una pendiente positiva, se marca primero la ordenada al origen. Luego, desde ese punto, se mueve hacia la derecha y se sube tantas unidades como lo indique la pendiente positiva.
¿Qué significa un denominador de 3 en la pendiente de la función lineal?
-Un denominador de 3 en la pendiente indica que, por cada 3 unidades que te mueves hacia la derecha, subes 2 unidades. Esto es porque la pendiente se expresa como una fracción, en este caso 2/3.
¿Qué relación tiene el signo de la pendiente con la dirección de la recta?
-El signo de la pendiente determina la dirección de la recta. Si la pendiente es positiva, la recta será creciente, y si es negativa, la recta será decreciente.
¿Qué ocurre si se tiene una pendiente de 2/3?
-Si la pendiente es 2/3, se mueve 3 unidades hacia la derecha y 2 unidades hacia arriba para graficar la recta, ya que la pendiente indica que por cada 3 unidades en el eje 'x', la recta sube 2 unidades en el eje 'y'.
¿Cómo se puede graficar una función lineal sin una calculadora?
-Para graficar una función lineal sin calculadora, primero se marca la ordenada al origen en el eje 'y'. Luego, se utiliza la pendiente para determinar cómo se mueve la recta, es decir, cuántas unidades se sube o baja por cada unidad que se mueve a la derecha. Uniendo los puntos obtenidos, se traza la recta.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Graficando una recta en la forma pendiente ordenada al origen

B2.03 Gráfica de la recta. Pendiente-ordenada al origen. (Parte 1 de 2)

Rectas paralelas y perpendiculares. Función lineal.

✂️📏📏RECTAS PARALELAS y PERPENDICULARES FUNCIÓN LINEAL | Juliana la Profe

Ecuaciones de la recta y sus transformaciones
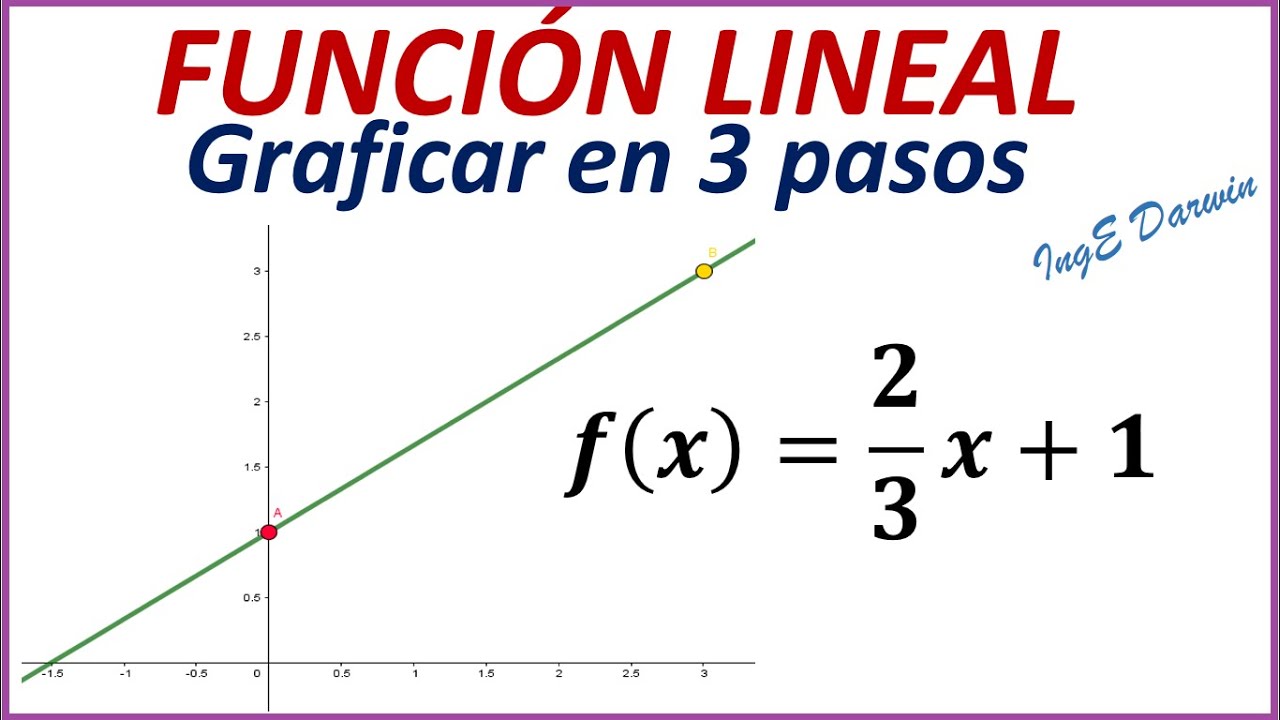
Graficar Funciones Lineales en 3 pasos (ordenada y pendiente) | Ejemplos
5.0 / 5 (0 votes)
