Graficar Funciones Lineales en 3 pasos (ordenada y pendiente) | Ejemplos
Summary
TLDREste video explica cómo graficar funciones lineales de manera fácil y rápida. Comienza recordando que las funciones lineales tienen una variable independiente de grado uno y un término independiente. Luego, el proceso se ejemplifica con tres funciones diferentes. Se muestran pasos para ubicar los puntos clave en el plano, utilizando el término independiente y el número que acompaña a la variable x, desplazándose en el eje y y en el eje x. También se destaca cómo manejar funciones sin término independiente, y se dan recomendaciones para tratar coeficientes decimales. Es un método práctico para graficar líneas rectas.
Takeaways
- 📊 Las funciones lineales tienen una variable independiente de grado uno y un término independiente.
- 📏 La gráfica de una función lineal es una línea recta, y basta con conocer dos puntos para graficarla.
- 📝 Se puede usar una tabla de valores o puntos de corte con los ejes, pero en este caso se utilizará un método más corto.
- 🟢 En la primera función f(x) = 2/3x + 1, el término independiente es 1 y se ubica en el eje y.
- 🔢 El numerador (2) indica el desplazamiento hacia arriba o abajo, y el denominador (3) indica el desplazamiento hacia la derecha.
- 📐 Después de marcar dos puntos en la gráfica, se unen con una regla para formar la recta.
- 🔴 En la segunda función g(x) = -4x + 2, el término independiente es 2, y se desplaza 4 unidades hacia abajo y 1 unidad a la derecha.
- ⚫ La tercera función y(x) = -5/2x no tiene término independiente, por lo que el primer punto es el origen.
- ⬇️ Se desplazan 5 unidades hacia abajo y 2 hacia la derecha para graficar la tercera función.
- 📎 Si el término independiente es cero, la función pasa por el origen, y es recomendable convertir decimales a fracciones.
Q & A
¿Qué característica principal tienen las funciones lineales?
-Las funciones lineales tienen la variable independiente 'x' de grado uno, es decir, con exponente 1, y un término independiente o un número sin variable.
¿Cómo es la gráfica de una función lineal?
-La gráfica de una función lineal es una línea recta.
¿Qué método se utiliza en el video para graficar una función lineal?
-Se utiliza un procedimiento basado en identificar el término independiente y el número que acompaña a la variable 'x' para ubicar los puntos en el plano y luego trazar la recta.
¿Qué representa el término independiente en una función lineal?
-El término independiente es el número que se ubica en el eje 'y' cuando 'x' es igual a cero.
En la función f(x) = (2/3)x + 1, ¿qué significa el numerador y el denominador del coeficiente 2/3?
-El numerador 2 indica cuántas unidades se desplaza hacia arriba (porque es positivo), y el denominador 3 indica cuántas unidades se desplaza hacia la derecha.
¿Cómo se traza la gráfica de la función f(x) = (2/3)x + 1?
-Primero se ubica el valor 1 en el eje 'y', luego se suben 2 unidades y se desplazan 3 unidades hacia la derecha para marcar el segundo punto. Finalmente, se trazan ambos puntos con una regla.
En la función g(x) = -4x + 2, ¿cómo se interpreta el coeficiente de 'x'?
-El coeficiente -4 indica que se deben bajar 4 unidades (por ser negativo) y luego desplazarse una unidad hacia la derecha.
¿Cómo se grafica la función g(x) = -4x + 2?
-Primero se ubica el 2 en el eje 'y', luego se bajan 4 unidades y se desplaza una unidad hacia la derecha para marcar el segundo punto. Finalmente, se trazan ambos puntos con una regla.
En la función y(x) = (-5/2)x, ¿qué indica que no haya un término independiente?
-Cuando no hay un término independiente, significa que la gráfica pasa por el origen de coordenadas (0,0).
¿Qué se recomienda hacer si el coeficiente de 'x' es un decimal?
-Se recomienda convertir el decimal a fracción y luego aplicar el mismo procedimiento para graficar la función.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Tutorial como crear encuestas en Google Drive Fácil y Rápido 2020

I - ¿Qué es una curva paramétrica? ¿Cómo la graficamos?

GRAFICAR FUNCIONES LINEALES PARTE 3 Super facil - Para principiantes

¿Qué es LA FUNCIÓN LINEAL? l Explicación sencilla l La pendiente l Ejemplos l Gráfica
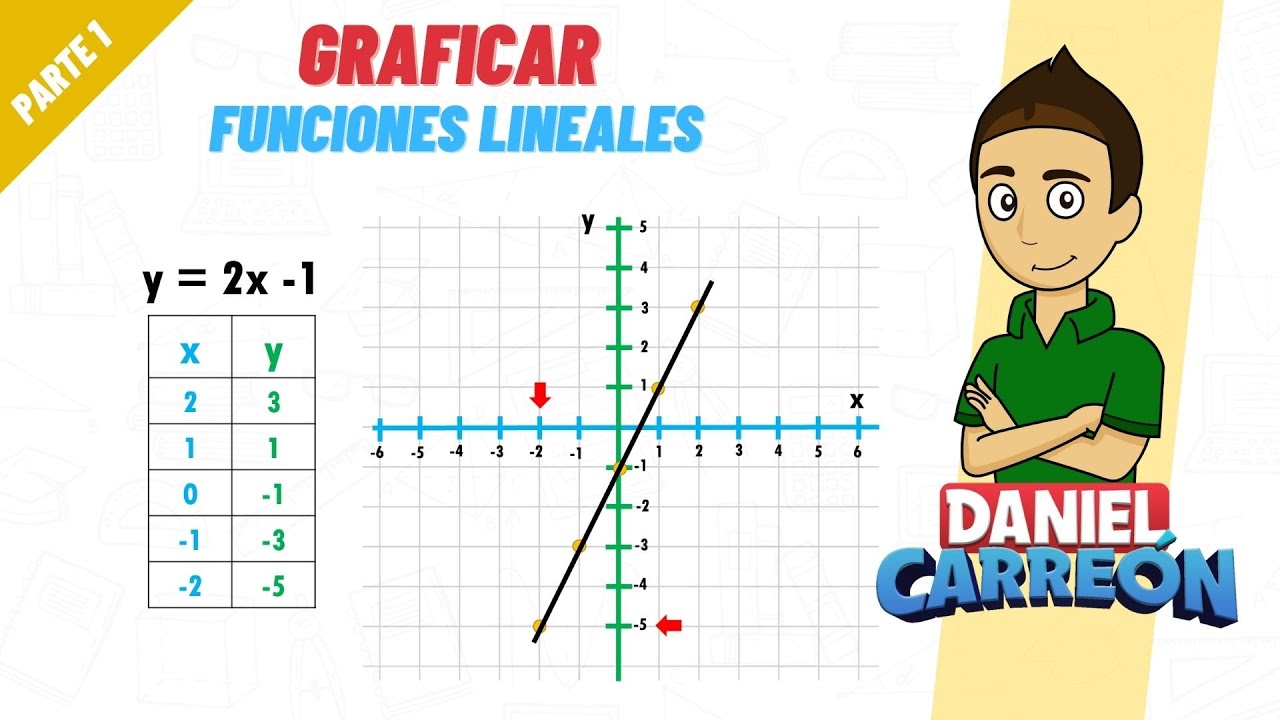
GRAFICAR FUNCIONES LINEALES PARTE 1

Sistemas de ecuaciones | Solución Método Gráfico | Ejemplo 2
5.0 / 5 (0 votes)
