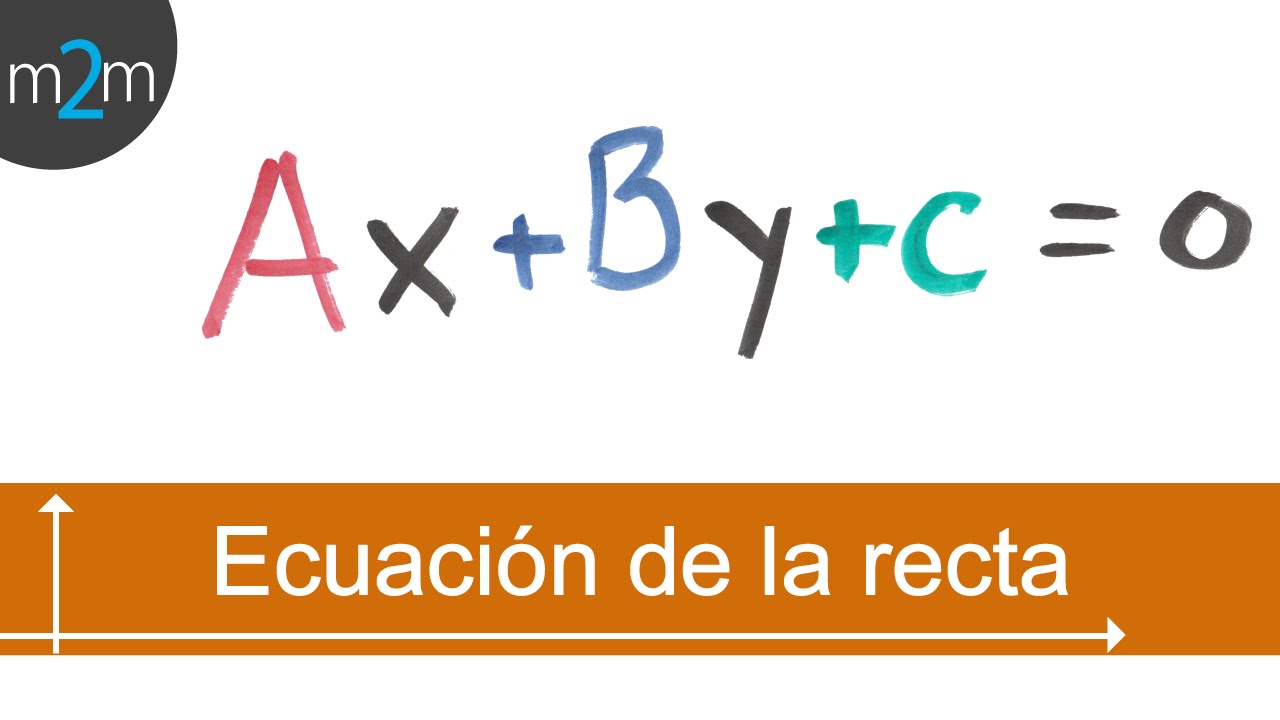Ecuaciones de la recta y sus transformaciones

Summary

En este video, se explica cómo trabajar con ecuaciones de la recta y sus transformaciones, utilizando diferentes formas, como la ecuación general y la forma punto-pendiente. Se detallan los pasos para calcular la pendiente, la abscisa al origen y la ordenada al origen, mediante ejemplos prácticos. El proceso incluye la sustitución de coordenadas en las fórmulas correspondientes, pasando de una forma a otra hasta obtener la ecuación final. A lo largo del ejercicio, se hace énfasis en la importancia de entender y aplicar las fórmulas de manera precisa para resolver problemas de rectas y sus transformaciones.

Takeaways

• 😀 La ecuación de la recta puede ser expresada usando dos puntos y la fórmula general, donde se sustituyen los valores de las coordenadas para encontrar la ecuación de la recta.
• 😀 La fórmula básica para la ecuación de una recta a partir de dos puntos es: (y - y1) = ((y2 - y1) / (x2 - x1)) * (x - x1).
• 😀 Se debe calcular la pendiente (m) primero, utilizando los valores de los puntos dados. En este caso, la pendiente resultó ser m = 3.
• 😀 Tras calcular la pendiente, se puede usar la fórmula de punto-pendiente para obtener la ecuación de la recta: y - y1 = m * (x - x1).
• 😀 En este caso, la ecuación de la recta derivada de los puntos dados fue simplificada a la forma general: 3x - 6 - y = -5.
• 😀 La forma general de la recta puede reordenarse para obtener una ecuación más sencilla: 3x - y - 5 = 0.
• 😀 Para convertir la ecuación de la recta a la forma pendiente-ordenada al origen, se despejan los términos adecuados, resultando en y = 3x - 5.
• 😀 Para calcular la ordenada al origen (b), se puede despejar de la ecuación general o utilizar la fórmula, resultando en b = -5.
• 😀 La abscisa al origen (la intersección de la recta con el eje X) se calcula utilizando la fórmula x = -c / a, obteniendo el valor x = 5/3.
• 😀 El proceso también puede utilizarse para encontrar la ecuación de la recta en su forma general a partir de la forma canónica o asimétrica.

Q & A

¿Cuál es la ecuación de la recta cuando se da por dos puntos?

La ecuación de la recta cuando se da por dos puntos se expresa como: (y - y1) = m(x - x1), donde m es la pendiente, calculada como (y2 - y1) / (x2 - x1).

¿Cómo se calcula la pendiente de la recta?

La pendiente (m) de la recta se calcula como la diferencia de las coordenadas y entre los dos puntos, dividida entre la diferencia de las coordenadas x: m = (y2 - y1) / (x2 - x1).

¿Qué se hace después de calcular la pendiente para obtener la ecuación en la forma general?

Una vez calculada la pendiente, se sustituye en la fórmula de la ecuación de la recta y se despeja para obtener la forma general, que es: Ax + By + C = 0.

¿Cómo se obtiene la forma general de la ecuación después de usar la fórmula punto-pendiente?

Para obtener la forma general, se multiplica la ecuación punto-pendiente por la pendiente y se reordenan los términos para tener la variable x y la variable y de un lado y un constante del otro lado, finalmente se iguala a cero.

¿Qué significa la ordenada al origen en el contexto de las ecuaciones de la recta?

La ordenada al origen es el valor de y cuando x es igual a cero, es decir, el punto en el que la recta corta el eje y.

¿Cómo se encuentra la ordenada al origen usando la ecuación en forma general?

Para encontrar la ordenada al origen, se sustituye x = 0 en la ecuación de la recta y se resuelve para y, lo que da el valor de la intersección con el eje y.

¿Cómo se obtiene la abscisa al origen?

La abscisa al origen es el valor de x cuando y es igual a cero. Se encuentra sustituyendo y = 0 en la ecuación de la recta y resolviendo para x.

¿Qué forma tiene la ecuación de la recta cuando se expresa en forma pendiente-intersección?

La forma pendiente-intersección de la ecuación de la recta es: y = mx + b, donde m es la pendiente y b es la ordenada al origen.

¿Qué es la forma canónica o asimétrica de una ecuación de la recta?

La forma canónica o asimétrica de la ecuación de la recta se refiere a una versión de la ecuación que involucra fracciones, y se usa para representar la ecuación de forma diferente a la forma general o pendiente-intersección.

¿Qué procedimiento se debe seguir si no se conocen los valores de la pendiente y la ordenada al origen?

Si no se conocen los valores de la pendiente y la ordenada al origen, se pueden calcular utilizando la fórmula de la pendiente a partir de dos puntos dados y luego derivar la ecuación en forma general a partir de la fórmula punto-pendiente.