Fungsi Transenden 2 (Invers Fungsi dan Turunannya)

Summary

This video explains the concept of inverse functions and their derivatives. It covers how to find the inverse of a function, including practical examples with polynomials and rational functions. The importance of monotonicity in ensuring a function has an inverse is emphasized, alongside the process of solving for an inverse algebraically. Additionally, the video discusses the relationship between the derivative of a function and the derivative of its inverse, highlighting the reciprocal rule. The content is geared towards students seeking a deeper understanding of functions, their inverses, and related calculus concepts.

Takeaways

• 😀 Inverse functions are obtained by solving for x in terms of y in a given function.
• 😀 A function has an inverse if it is one-to-one (bijective), meaning it passes the horizontal line test or is strictly monotonic (either increasing or decreasing).
• 😀 The inverse of a linear function, like y = 2x, is easily found by solving for x (e.g., x = y/2).
• 😀 Not all functions have an inverse. For example, y = x² doesn’t have an inverse unless the domain is restricted (e.g., x ≥ 0).
• 😀 Derivatives help determine if a function is monotonic (always increasing or decreasing), which is necessary for the existence of an inverse.
• 😀 The derivative of a function f(x) = x⁵ + 2x + 1 is f'(x) = 5x⁴ + 2, which is always positive, indicating the function is strictly increasing and thus has an inverse.
• 😀 The relationship between a function and its inverse can be understood graphically, where the graph of the inverse is a reflection of the original function over the line y = x.
• 😀 To find the derivative of an inverse function, the formula is (f⁻¹)'(x) = 1 / f'(f⁻¹(x)). This shows that the derivative of the inverse is the reciprocal of the derivative of the original function.
• 😀 To find the inverse of a rational function, such as y = x / (1 - x), you can manipulate the equation algebraically to solve for x in terms of y.
• 😀 The process of finding an inverse function includes three main steps: (1) set y = f(x), (2) solve for x to express the inverse, (3) replace y with x in the final expression to get f⁻¹(x).

Q & A

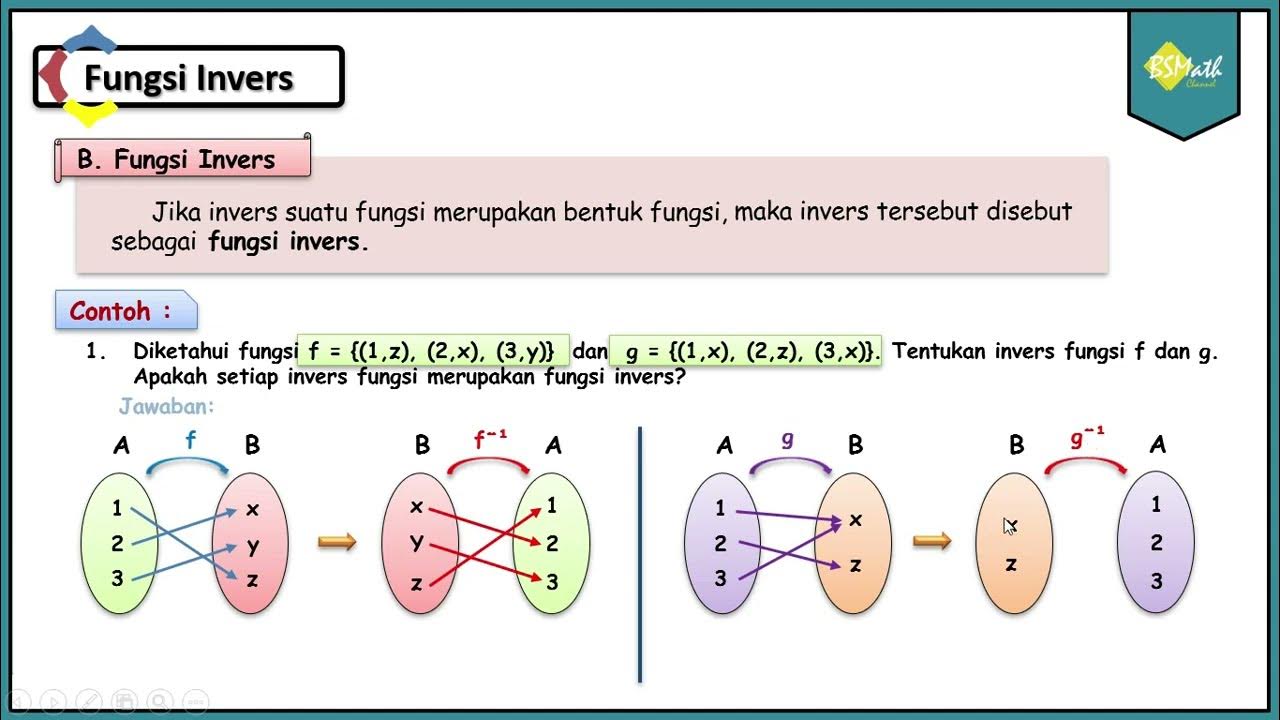
What is an inverse function?

An inverse function reverses the operation of the original function. If a function maps an input 'x' to an output 'y', then its inverse maps 'y' back to 'x'.

How do you find the inverse of a function?

To find the inverse of a function, replace the output variable (usually 'y') with the input variable (usually 'x'), solve for 'x', and then replace 'y' with 'x' in the final expression.

What is the condition for a function to have an inverse?

A function must be one-to-one, meaning that for any two distinct values of 'x', the outputs must also be distinct. This ensures that each 'y' value corresponds to only one 'x' value.

What does it mean for a function to be monotonically increasing or decreasing?

A monotonically increasing function consistently increases as 'x' increases, and a monotonically decreasing function consistently decreases as 'x' increases. These types of functions are one-to-one and thus have an inverse.

How can we determine if a function is monotonically increasing or decreasing?

To check if a function is monotonically increasing or decreasing, examine its derivative. If the derivative is positive for all values of 'x', the function is increasing. If the derivative is negative, the function is decreasing.

Why does the function f(x) = x^2 not have an inverse?

The function f(x) = x^2 is not one-to-one because for some values of 'y', there are multiple corresponding values of 'x'. For example, both x = 1 and x = -1 give f(x) = 1, so it fails the one-to-one criterion.

What is the relationship between the derivatives of a function and its inverse?

The derivative of the inverse function is the reciprocal of the derivative of the original function, evaluated at the inverse of 'x'. Mathematically, this is expressed as: (f^{-1})'(x) = 1 / f'(f^{-1}(x)).

How do you find the derivative of an inverse function using an example?

To find the derivative of an inverse function, first find the derivative of the original function, then evaluate it at the point corresponding to the inverse. For example, if f(x) = x^5 + 2x + 1, its derivative is f'(x) = 5x^4 + 2. If f(1) = 4, we substitute x = 1 into f'(x) to get f'(1) = 7, so the derivative of the inverse at x = 4 is 1/7.

What is the graphical interpretation of an inverse function?

The inverse of a function can be visualized as the reflection of the original function across the line y = x. This means that for each point (a, b) on the original function, there is a corresponding point (b, a) on the inverse function.

How do you compute the inverse of a rational function, such as f(x) = x / (1 - x)?

To compute the inverse of f(x) = x / (1 - x), you start by setting y = x / (1 - x), then solve for x in terms of y. After simplifying, you find that the inverse is f^-1(y) = y / (1 - y). Finally, replace 'y' with 'x' to obtain the inverse function in terms of 'x'.