Lec 52 - Logarithmic Functions
Summary
TLDRThis educational video delves into the inverse of exponential functions, focusing on their properties, graphs, and the domain and range of these inverse functions. It introduces the concept of logarithmic functions as the inverse of exponential functions, explains the '7 rule' for understanding their one-to-one correspondence, and illustrates how to determine the domain and range of basic and derived logarithmic functions. The video also demonstrates the reversibility of logarithmic and exponential functions through examples and discusses the graphical representation of these inverse functions, emphasizing the reflection along the line y=x.
Takeaways
- 📚 The video discusses the inverse of exponential functions, focusing on their properties, graphs, and the domain and range of these inverse functions.
- 🔍 An exponential function is defined as f(x) = a^x, with conditions that 'a' must be greater than 0 and not equal to 1 to ensure the function is one-to-one and has an inverse.
- 🔄 The inverse of an exponential function is a logarithmic function, denoted as log_a(x), and is defined as the inverse of a^x.
- 📉 The domain of the exponential function (a^x) is all real numbers, and its range is from 0 to infinity, not including negative values.
- 📈 The range of the logarithmic function is all real numbers, while its domain is from 0 to infinity, not including 0 and negative values.
- 🔢 The '7 rule' is introduced as a memory technique to recall the one-to-one correspondence between logarithmic and exponential functions: if y = log_a(x), then x = a^y.
- 📝 The script verifies that the logarithmic function is indeed the inverse of the exponential function by applying the rules f(f^-1(x)) = x and f^-1(f(x)) = x.
- 🤔 The importance of understanding the domain and range of both exponential and logarithmic functions is emphasized for problem-solving and function composition.
- 📉 The video explains how to determine the domain of more complex functions composed with logarithms, such as log_a(1-x), by ensuring the argument of the logarithm is within its valid domain.
- 📈 The script demonstrates the reversibility of logarithmic and exponential functions with examples, showing how to find values and solve equations using their inverse relationship.
- 📊 The video concludes with a discussion on graphing the inverse functions, describing the process of reflecting the graph of the exponential function across the line y=x to obtain the logarithmic function's graph.
Q & A
What is the main focus of the video?
-The video focuses on the inverse of exponential functions, discussing their properties, graphs, and the relationship between domain and range of these inverse functions.
What is an exponential function?
-An exponential function is a function of the form f(x) = a^x, where 'a' is a base that is greater than 0 and not equal to 1.
Why is the base 'a' in an exponential function restricted to be greater than 0 and not equal to 1?
-The restriction on 'a' being greater than 0 and not equal to 1 ensures that the function is one-to-one and has an inverse. If 'a' were 1, the function would be constant and not interesting to study as it would not have an inverse.
What is the definition of a logarithmic function?
-A logarithmic function to the base 'a' is defined as y = log_a(x), where 'x' is the argument of the function and it is the inverse of the exponential function f(x) = a^x.
What is the '7 rule' mentioned in the video?
-The '7 rule' is a mnemonic to remember the one-to-one correspondence between logarithmic and exponential functions. It states that if y = log_a(x), then x = a^y.
How can you verify if a function is the inverse of another function?
-You can verify if a function is the inverse by checking if f(f^-1(x)) = x and f^-1(f(x)) = x, where f^-1 represents the inverse function.
What are the domain and range of the logarithmic function?
-The domain of the logarithmic function is (0, ∞), meaning it cannot have negative values or zero. The range of the logarithmic function is the entire set of real numbers.
How does the domain of a function affect its graph?
-The domain of a function determines the set of all possible input values for which the function is defined. This directly affects the graph of the function, as the graph will only include points that correspond to values within the domain.
What is the relationship between the graph of an exponential function and its inverse logarithmic function?
-The graph of the inverse logarithmic function is the reflection of the original exponential function along the line y = x. This means the graphs are mirror images of each other across this line.
How can you use logarithmic functions to solve problems involving exponents?
-You can use the property that a^(log_a(x)) = x to solve problems. For example, if you know a^y = x and you want to find y, you can use log_a(x) to find that y = log_a(x).
What is the significance of the base 'a' in the logarithmic function in relation to the domain?
-The base 'a' of the logarithmic function determines the range of the original exponential function, which in turn becomes the domain of the logarithmic function. This means that the logarithmic function is defined for arguments greater than zero.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

FUNCTION (IGCSE/GCE O Level ADD MATHS) 0606

REPRESENTATIONS OF AN INVERSE FUNCTIONS | General Mathematics | Quarter 1 - Module 13
(Part 1) FUNGSI KOMPOSISI DAN FUNGSI INVERS MATEMATIKA SMA KELAS 11 #kurikulummerdeka #matematikasma

Fungsi Komposisi dan Fungsi Invers SMA/MA/SMK

Evaluating Inverse Trigonometric Functions
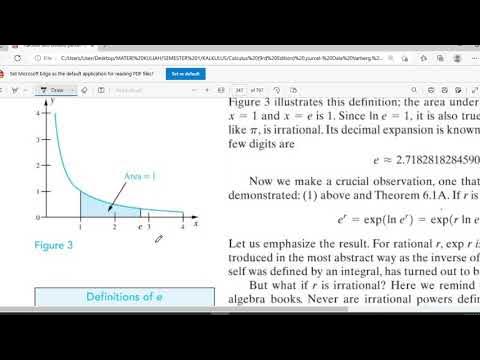
Fungsi Transenden 3 (Fungsi Eksponensial Natural)
5.0 / 5 (0 votes)