Fungsi Hiperbolik dan Balikannya
Summary
TLDRThis lecture on calculus focuses on hyperbolic functions, their derivatives, and inverses. Key topics include the definitions and formulas for hyperbolic sine, cosine, and tangent functions, along with their respective derivatives. The session also covers the inverse hyperbolic functions, including their formulas and how to derive them. The professor illustrates the concepts with examples, such as solving equations involving hyperbolic functions and finding their derivatives. Students are encouraged to practice solving related problems to gain a deeper understanding of the material.
Takeaways
- 😀 The lecture begins with an introduction to hyperbolic functions, including definitions and formulas for sinh(x), cosh(x), and tanh(x).
- 😀 The definition of the hyperbolic sine function is given as sinh(x) = e^x - e^(-x) / 2, and similar formulas for cosh(x) and tanh(x) are provided.
- 😀 The lecture covers the derivatives of hyperbolic functions, such as the derivative of sinh(x) being cosh(x) and the derivative of cosh(x) being sinh(x).
- 😀 Several examples of hyperbolic function derivatives are shown, highlighting the similarities with regular trigonometric functions.
- 😀 A proof is provided showing that e^(2x) = cosh(2x) + sinh(2x) by expanding the expressions and simplifying.
- 😀 The concept of inverse hyperbolic functions is introduced, with examples like sinh^(-1)(x) and how they are derived.
- 😀 The lecture emphasizes that the inverse functions of hyperbolic functions can be found using logarithms and square roots, as shown in the example with sinh^(-1)(x).
- 😀 Detailed steps are given for calculating the inverse of the sinh function, with a focus on solving for x and simplifying the expressions.
- 😀 Derivatives of inverse hyperbolic functions are explained, such as the derivative of sinh^(-1)(x) being 1/√(x^2 + 1).
- 😀 Several practice problems are provided for the students to work through, including derivative and integral problems involving hyperbolic functions and their inverses.
Q & A
What is the definition of hyperbolic sine function (sinh)?
-The hyperbolic sine function, denoted as sinh(x), is defined by the formula sinh(x) = (e^x - e^(-x))/2, where e is the base of the natural logarithm.
How is the hyperbolic cosine function (cosh) defined?
-The hyperbolic cosine function, cosh(x), is defined by the formula cosh(x) = (e^x + e^(-x))/2. It is closely related to the hyperbolic sine function.
What is the relationship between the hyperbolic tangent function (tanh) and hyperbolic sine and cosine?
-The hyperbolic tangent function, tanh(x), is the ratio of sinh(x) to cosh(x), i.e., tanh(x) = sinh(x)/cosh(x).
What is the derivative of the hyperbolic sine function?
-The derivative of sinh(x) is cosh(x), i.e., d/dx [sinh(x)] = cosh(x).
What is the derivative of the hyperbolic cosine function?
-The derivative of cosh(x) is sinh(x), i.e., d/dx [cosh(x)] = sinh(x).
How does the derivative of the hyperbolic tangent function (tanh) differ from its trigonometric counterpart?
-The derivative of tanh(x) is sech^2(x), whereas the derivative of the regular tangent function is sec^2(x). The hyperbolic tangent function's derivative involves the hyperbolic secant function, sech(x), instead of the standard secant.
What is the inverse of the hyperbolic sine function (sinh^(-1))?
-The inverse of the hyperbolic sine function, denoted as sinh^(-1)(x), is given by the formula sinh^(-1)(x) = ln(x + √(x² + 1)), where ln is the natural logarithm.
What is the key difference between hyperbolic functions and trigonometric functions?
-The key difference is that hyperbolic functions, like sinh, cosh, and tanh, are based on exponential functions involving e^x and e^(-x), while trigonometric functions are based on the unit circle and involve sine, cosine, and tangent functions with respect to angles.
How do you differentiate the inverse hyperbolic cosine function?
-The derivative of the inverse hyperbolic cosine function, cosh^(-1)(x), is given by d/dx [cosh^(-1)(x)] = 1/√(x² - 1), for x ≥ 1.
What is the application of the derivative of inverse hyperbolic functions in calculus problems?
-The derivatives of inverse hyperbolic functions are useful for solving integrals and differentiating functions involving expressions such as sqrt(x² ± 1), which commonly arise in calculus problems.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Derivatives of Inverse Hyperbolic Functions

Matematika Teknik I: 101 Fungsi Logaritma Natural - Definisi ln x dan turunannya

Diferensial Fungsi Sederhana

Fungsi Naik, fungsi turun, nilai stasioner, titik stasioner, nilai maksimum dan minimum suatu fungsi
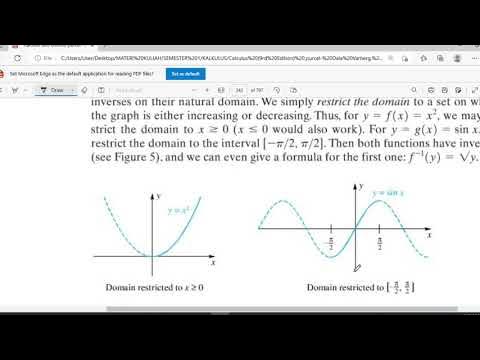
Fungsi Transenden 2 (Invers Fungsi dan Turunannya)

Higher Order Derivatives
5.0 / 5 (0 votes)