Kenapa jalur melengkung ini lebih pendek daripada jalur lurus? (Dr STONE S4)

Summary

In this video, the concept of geodesics, or the shortest path between two points on a curved surface, is explained using the example of the Earth’s spherical shape. The script demonstrates how, unlike on flat surfaces where straight lines are the shortest distance, the shortest path on the Earth is a curved line that follows the surface. This concept is illustrated with a reference to *Dr. Stone* Season 4, Episode 1, where the path between Japan and the U.S. is shown to be a curved geodesic, despite appearing straight on flat maps. The explanation blends mathematical principles and real-world examples to showcase the fascinating nature of curved geometry.

Takeaways

• 😀 The shortest distance between two points on a flat surface is a straight line.
• 😀 On a curved surface like the Earth, the shortest path between two points is a geodesic (a curved line).
• 😀 The *Doctor Stone* anime episode illustrates the comparison between straight-line distance and geodesic on Earth.
• 😀 A straight line on a flat map distorts the actual shortest path on Earth's spherical surface.
• 😀 Geodesics are the true shortest paths on curved surfaces, like the Earth's surface, and are different from straight lines.
• 😀 When comparing straight-line and curved paths from Japan to America, the geodesic is often shorter than the straight-line path.
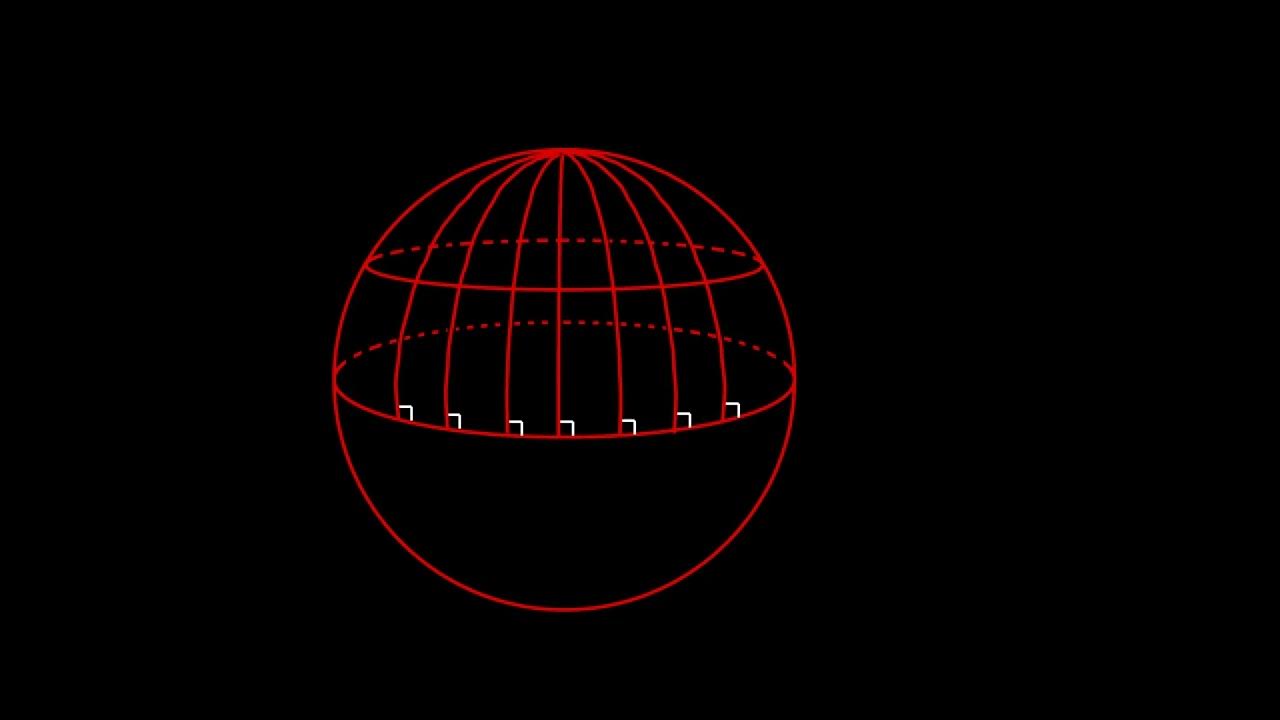
• 😀 The Earth is spherical, so calculating distances between two points requires spherical geometry, not flat-plane geometry.
• 😀 The concept of geodesics can be understood by visualizing a great circle that connects two points and passes through the center of the Earth.
• 😀 The *Doctor Stone* scene inaccurately depicts a straight line as the shortest path when, in fact, it is the curved geodesic path that’s shorter.
• 😀 The shortest distance on a sphere (like Earth) involves traveling along a curved path, which looks straight when viewed from the sphere's center.

Q & A

What is the concept of the shortest distance between two points on a flat surface?

The shortest distance between two points on a flat surface is a straight line, which can be demonstrated using calculus or by directly measuring the distance.

How does the concept of the shortest distance change when applied to the Earth's surface?

On the Earth's surface, which is curved, the shortest path between two points is no longer a straight line but a curved path known as a geodesic.

What is a geodesic?

A geodesic is the shortest path between two points on a curved surface, such as the Earth's spherical surface.

Why is the straight line not the shortest distance on the Earth’s surface?

Because the Earth is a curved surface, a straight line does not represent the shortest path. The shortest path must follow the curve of the Earth's surface, which is a geodesic.

What example is used in *Doctor Stone* to explain the concept of geodesics?

In *Doctor Stone*, the characters compare the distances between Japan and America, measuring both a straight line and a curved path. It is shown that the curved path is shorter.

Why does the curved path appear shorter than the straight line in the example from *Doctor Stone*?

The curved path is shorter because it follows the actual shape of the Earth's surface, which is spherical. The straight line doesn't reflect the Earth's curvature, leading to a longer distance.

What mistake is pointed out in the *Doctor Stone* anime regarding the straight line on the globe?

The mistake in the anime is that the straight line is incorrectly treated as the shortest path, whereas the true shortest path is along the curved geodesic.

How is the shortest path on a sphere different from a flat surface?

On a sphere, the shortest path between two points follows the curve of the surface, unlike on a flat surface where the shortest distance is a straight line.

What role does a circle play in determining the shortest path on the Earth’s surface?

To determine the shortest path between two points on a spherical surface, a circle is drawn centered on the sphere's center, passing through both points. This circle represents the geodesic, the shortest path between the points.

How is the geodesic concept practically applied in navigation?

In navigation, the geodesic is used to determine the shortest route between two locations on Earth, such as when planning flight paths or maritime routes, which often follow curved lines on maps.