The Maths of General Relativity (3/8) - Geodesics

Summary

This episode of Science Clique explores the mathematics of general relativity through the concept of geodesics. It explains how objects in the universe naturally follow the straightest possible paths, or geodesics, when no external forces are applied. The video delves into the evolution of an object's velocity over time, using the geodesic equation to predict an object's trajectory. It introduces Christoffel symbols, which are crucial for understanding how coordinates behave in the presence of a grid's structure. The analogy of an airplane's flight over the Earth's curved surface illustrates the concept of geodesics and the impact of coordinate systems on perceived motion.

Takeaways

• 🌌 The video discusses the mathematics of general relativity, focusing on the concept of geodesics.
• 📏 In the absence of external forces, objects in the universe naturally move in straight lines, which are represented as geodesics in spacetime.
• ⏱️ The evolution of an object's velocity over proper time can predict its trajectory, with the velocity vector remaining constant along the geodesic.
• 🔄 The concept of a geodesic is introduced as the natural path an object follows, which is a straight line in the context of spacetime.
• 🧭 The velocity vector's derivative with respect to proper time is zero along the geodesic, indicating no acceleration.
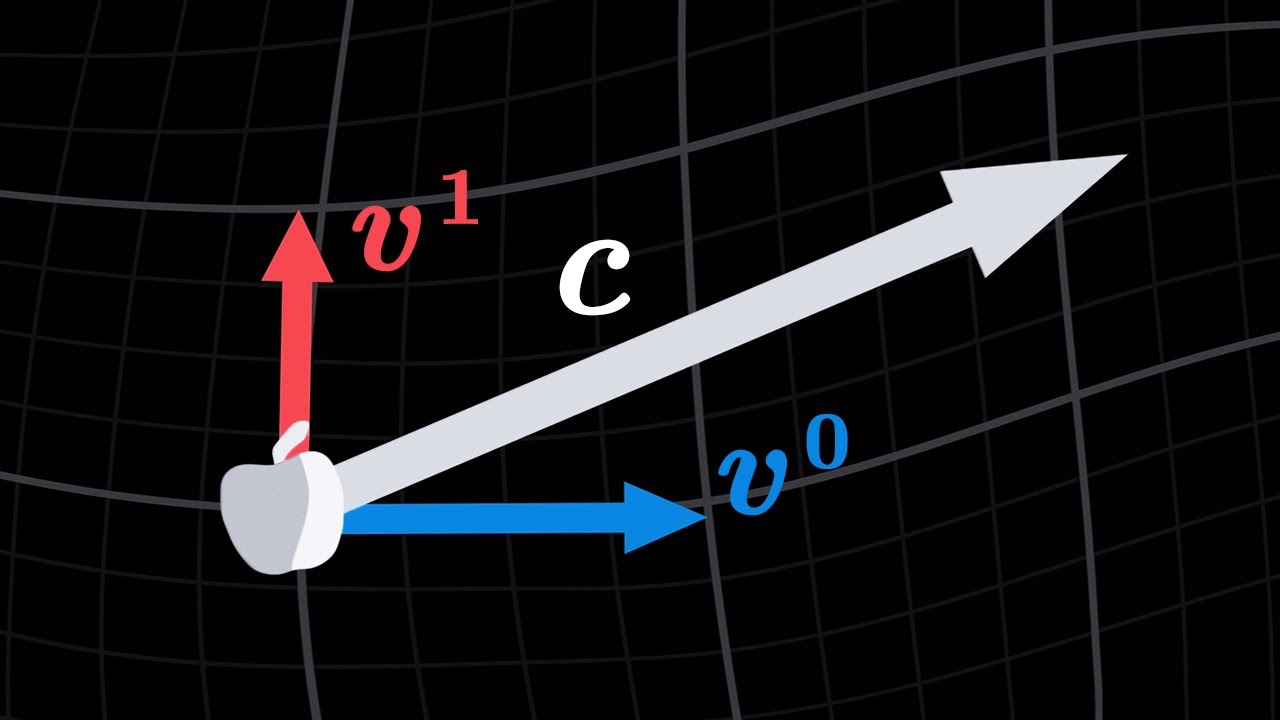
• 📐 The velocity vector can be decomposed into components and basis vectors, which can change due to the choice of coordinate system.
• 🌐 The basis vectors' variation along the trajectory is influenced by the grid or coordinate system used, which can be irregular.
• 🔢 The rate of change of the basis vectors is described by the Christoffel symbols, which are crucial for general relativity as they encode the grid's structure.
• 🌍 The video uses the Earth's surface with latitude and longitude coordinates as an analogy to explain how geodesics can appear curved due to the coordinate system used.
• ✈️ An airplane flying in a straight line along a great circle on Earth is given as an example of a geodesic, where the trajectory appears curved on a grid but is actually straight.

Q & A

What is the concept of a geodesic in the context of general relativity?

A geodesic in general relativity is the natural path that a point mass moves along in spacetime, which is the shortest path between two points in a curved spacetime. It represents the trajectory that an object follows when no force is applied to it.

Why do objects in the universe tend to move in straight lines when no force is applied?

Objects in the universe tend to move in straight lines when no force is applied due to the symmetry of spacetime. There is no reason for the object to turn one way or the other, so it follows the path of least resistance, which is a straight line in the absence of external influences.

What is the significance of the velocity vector in describing the motion of an object?

The velocity vector is significant in describing the motion of an object because it indicates the direction and speed at which the object moves through spacetime. It is a fundamental quantity used to predict the trajectory of an object as proper time passes.

How does the concept of proper time relate to the motion of objects in spacetime?

Proper time is the time measured by a clock moving with an object, and it is the parameter used to describe the motion of objects in spacetime. The evolution of an object's velocity vector is described as proper time passes, allowing for the prediction of the object's trajectory.

What is the role of basis vectors in the geodesic equation?

Basis vectors play a crucial role in the geodesic equation as they form the coordinate system within which the motion of objects is described. They help in expressing the velocity vector and its components, which are essential for understanding the trajectory of an object.

Why do basis vectors change along the trajectory in an irregular coordinate system?

Basis vectors change along the trajectory in an irregular coordinate system because the grid or coordinate system itself can be irregular. This means that the basis vectors' components can vary as the object moves through spacetime.

What are Christoffel symbols and how are they used in the geodesic equation?

Christoffel symbols, denoted by the capital Greek letter gamma (Γ), are quantities that encode how a coordinate grid changes along different directions. They are used in the geodesic equation to express the rate of change of the velocity vector components as proper time passes.

How does the geodesic equation help in predicting the trajectory of an object?

The geodesic equation helps in predicting the trajectory of an object by providing a mathematical framework to calculate the rate of change of each component of the velocity vector as proper time passes. This allows for the prediction of the object's path throughout spacetime.

What is the example used in the script to illustrate the concept of geodesics?

The script uses the example of an airplane flying on the surface of the Earth, using a latitude-longitude coordinate system. The airplane's trajectory forms a great circle, which is a geodesic, and it demonstrates how a straight path can appear curved when plotted on a grid that does not correspond to straight lines on a sphere.

Why does the airplane's trajectory appear curved when plotted on a latitude-longitude coordinate system?

The airplane's trajectory appears curved on a latitude-longitude coordinate system because the Earth's surface is a sphere, and the grid of latitude and longitude lines does not represent straight lines on a spherical surface. The geodesic, or the shortest path, appears as a great circle, which is a curve on the surface of the Earth.

What do the Christoffel symbols measure in the context of the Earth's surface analogy?

In the context of the Earth's surface analogy, the Christoffel symbols measure the extent to which the coordinates deviate from straight lines along the grid. They indicate how the basis vectors change as they are transported along the grid, which is essential for understanding the curvature of the Earth's surface.

Outlines

00:00

🌌 Understanding Geodesics in General Relativity

This paragraph introduces the concept of geodesics in the context of general relativity. It explains that in the absence of external forces, objects in the universe naturally move in straight lines, which are represented as geodesics in the fabric of spacetime. The paragraph discusses how the velocity vector of an object remains constant along its geodesic path, implying that there is no acceleration. It further elaborates on how the basis vectors, which define the coordinate system, can change along the trajectory due to the curvature of spacetime. The christoffel symbols are introduced as a means to quantify how these basis vectors change, which is crucial for understanding the behavior of objects in a gravitational field. The geodesic equation is mentioned as a fundamental tool for predicting the trajectory of objects through spacetime.

05:00

🌍 Geodesics on the Earth's Surface

The second paragraph uses the analogy of the Earth's surface to illustrate the concept of geodesics. It describes how an airplane flying in a straight line follows a great circle route, which is a geodesic on the Earth's surface. The paragraph explains that while the airplane's velocity vector remains constant, the trajectory appears curved when plotted on a latitude-longitude coordinate system due to the spherical shape of the Earth. The christoffel symbols are again discussed, but this time in the context of how they measure the deviation of coordinates from straight lines on a curved surface. The paragraph concludes by emphasizing that the christoffel symbols are essential for understanding the behavior of coordinates and the underlying geometry of spacetime.

Keywords

💡General Relativity

General Relativity is a theory of gravitation developed by Albert Einstein, published in 1915. It is the current description of gravity as a geometric property of spacetime caused by the uneven distribution of mass. In the video, General Relativity is the overarching framework for understanding how objects move through spacetime, particularly in the context of geodesics.

💡Geodesics

A geodesic is the shortest path between two points in a curved space, such as a great circle on the Earth's surface. In the context of General Relativity, geodesics describe the natural path that a freely moving object will take through spacetime. The video explains that all objects in the universe tend to follow geodesics, which are straight lines in the absence of external forces.

💡Proper Time

Proper time is the time measured by a clock moving along with an object, which is the time experienced by that object. It is used to describe the aging of an object under the influence of gravity or acceleration. In the video, the evolution of an object's velocity is described as it passes through proper time, which is key to predicting the object's trajectory.

💡Velocity Vector

The velocity vector is a mathematical representation of an object's velocity, indicating both the speed and direction of the object's motion. In the video, the velocity vector is used to describe how an object moves through spacetime, and its constancy along a geodesic implies that the object is in free-fall, experiencing no acceleration.

💡Symmetry

Symmetry in physics often refers to the invariance of physical laws under certain transformations. In the video, the concept of symmetry is used to explain why, in the absence of forces, an object's world line through spacetime tends to be straight, as there is no reason for it to deviate from a straight path.

💡Basis Vectors

Basis vectors are the fundamental vectors that define a coordinate system. They are used to express any vector in terms of the coordinate system. In the video, basis vectors are used to decompose the velocity vector and to understand how the components of the velocity vector change as the object moves through spacetime.

💡Christoffel Symbols

Christoffel symbols, denoted by the Greek letter gamma (Γ), are mathematical objects that encode the rate of change of the basis vectors of a coordinate system. They are crucial in General Relativity for describing how the coordinates of spacetime are curved. The video explains that these symbols are essential for understanding how the grid or coordinate system changes along with the object's trajectory.

💡Coordinate System

A coordinate system is a method of specifying points in space by using numbers, often in a grid-like structure. In the video, the coordinate system is used to describe how basis vectors and their changes can be measured, and how these changes relate to the motion of objects along geodesics.

💡Non-accelerating

Non-accelerating motion refers to the movement of an object where its velocity does not change over time. In the video, it is mentioned that objects in free-fall follow geodesics and experience non-accelerating motion, meaning their velocity vector does not change direction or magnitude as they move through spacetime.

💡Derivative

The derivative in mathematics is a measure of how a function changes as its input changes. In the context of the video, derivatives are used to describe the rate of change of the velocity vector with respect to proper time and how the basis vectors change along the trajectory of an object.

💡Great Circle

A great circle is the largest circle that can be drawn on the surface of a sphere, such as the Earth. In the video, the concept of a great circle is used as an analogy to explain geodesics. An airplane flying in a straight line along a great circle is following a geodesic, even though its path appears curved when plotted on a two-dimensional map.

Highlights

Exploring the mathematics of general relativity through the concept of geodesics.

Defining world lines and the motion of objects as proper time progresses.

Understanding velocity as a directional indicator through space-time.

Describing the evolution of velocity to predict the trajectory shape in the universe.

Objects naturally move in straight lines when no force is applied, forming straight world lines.

The concept of geodesics as the natural trajectory formed by transporting velocity along itself.

In a geodesic, the velocity vector does not turn, indicating non-accelerating natural movement.

Deriving the relationship between the change in velocity components and basis vectors.

Basis vectors can vary due to the irregularity of the chosen coordinate system.

Evolution of a basis vector along the world line and its decomposition into coordinate components.

Introducing the new quantity that indicates how the basis vector varies along a coordinate.

The importance of the vector derivative of the basis vector with respect to a coordinate.

Defining Christoffel symbols and their role in general relativity.

Christoffel symbols encode how the grid changes and provide information on coordinate behavior.

Formulating the geodesic equation using Christoffel symbols to predict object trajectories.

Illustrating the concept of geodesics using the surface of the Earth and a latitude-longitude coordinate system.

The geodesic trajectory of an airplane moving in a straight line forms a great circle around the Earth.

Christoffel symbols measure the deviation of coordinates from straight lines on a spherical grid.

Transcripts

[Music]

welcome back to science clique

today the mathematics of general

relativity

part 3 geodesics

in the previous videos we have defined

the concepts of world lines

motion as proper time goes by and

velocity

which indicates the direction in which

an object moves through space and time

we would now like to describe the

evolution of this velocity

as proper time passes in order to

predict the shape of the trajectory

in our universe objects naturally move

in straight lines

when no force is applied world lines

tend to be straight

through the dimensions of space and time

this comes from the symmetry of such

trajectory

an object has no reason to turn one way

or the other

this simple consideration gives us a

method to predict the trajectory of a

body

as soon as we know its velocity at a

given instant we can just transport the

arrow along

itself to gradually predict the movement

of the object

this type of trajectory which is formed

by transporting velocity along itself

is called a geodesic

[Music]

in the universe all objects tend to

follow geodesics

on a geodesic the vector does not turn

we can thus write that its derivative

with respect to proper time

is zero along the trajectory

the velocity vector of the apple does

not vary

this equation simply says that the

natural movement of bodies

is non-accelerating and therefore that

when they experience no

force objects tend to move straight

ahead

but we saw previously that the velocity

vector can be written as the sum of its

components

multiplied by the basis vectors

[Music]

using this expression and knowing that

the derivative of a product

is the sum of each term multiplied by

the derivative of the other term

we obtain a relation between on one side

the change in the components of the

velocity

and on the other side the change in the

basis vectors themselves

the basis vectors can indeed vary

throughout the trajectory

because the grid that we choose as our

coordinate system can very well be

irregular

although the vector remains the same as

a geometric object

its components on the grid can vary as

the apple moves

when we think about it the evolution of

a basis vector along the world line

can be decomposed as the sum of its

evolution

along each of the two coordinates

multiplied by the speed of the apple

because the faster the apple moves

the faster the basis vector will vary

[Music]

for each coordinate this gives us a new

quantity

which indicates how the basis vector

varies along the coordinate

this variation is expressed as a vector

that is the derivative of the basis

vector with respect to the coordinate in

question

this vector is very interesting because

it no longer depends on the trajectory

but only on the structure of the grid

itself

this vector can be expressed through its

components

denoted by the capital letter gamma

in our two-dimensional case these

components

exist in eight different versions two

components

for four different vectors these numbers

are called christopher symbols the

christopher symbols are essential

quantities for general relativity

because they encode how the grid changes

along each

direction they contain crucial

information

on how our coordinates behave

[Music]

rewriting the previous equation using

christopher symbols

we finally get to the geodesic equation

this very important equation allows us

to calculate for

each component of the velocity its rate

of change

as proper time passes

the geodesic equation thus allows us to

predict the whole trajectory of an

object

as long as we know its velocity at a

given moment

and the value of each christopher symbol

all throughout the grid

to illustrate all these ideas let's

imagine not a space-time

but simply the surface of the earth

we decide to use a latitude longitude

coordinate system

which at first glance seems to be a very

good fit for the geometry

now imagine that an airplane is moving

in a straight line

when an object moves straight ahead

without ever turning

its trajectory forms what is called a

geodesic

in our situation the geodesic is a great

circle around the planet

on this geodesic trajectory the airplane

is always moving straight ahead

its velocity vector does not change

orientation

but when we plot the coordinates the

trajectory seems

curved the airplane seems to change

orientation along the grid

in reality its trajectory is perfectly

straight

the problem does not come from the

airplane but from our grid

it's our coordinates that are curved

their axes do not correspond

to straight lines on a sphere compared

to real straight lines

geodesics they turn

starting from a basis vector and

transporting it along the grid

we can measure how much this vector

changes by another vector

it's the components of this vector that

are called christophel symbols

the christopher symbols measure the

extent to which our coordinates deviate

from straight lines

along the grid

[Music]

you