Construire l'image d'une figure par une translation (1) - Quatrième/Troisième
Summary
TLDRDans cette vidéo, l'enseignant explique comment construire l'image d'une figure par translation. Après un rappel rapide sur la définition de la translation comme un glissement dans une direction et sur une distance données, il montre concrètement comment appliquer cette transformation à un triangle. L'exercice consiste à déterminer l'image des points A, B, et C du triangle par une translation définie par deux points, M et N. Le processus comprend la construction de droites parallèles et le report des distances pour obtenir les points translatés. Enfin, les points sont reliés pour former l'image du triangle.
Takeaways
- 😀 Une translation est un glissement où une figure est déplacée dans une direction donnée sur une distance précise.
- 😀 La translation est définie par un vecteur, qui est une flèche représentant la direction et la distance du glissement.
- 😀 Le mot 'flèche' utilisé pour décrire la direction d'une translation sera plus tard remplacé par le terme 'vecteur' en mathématiques.
- 😀 Pour construire l'image d'une figure par une translation, on doit construire l'image de chaque point de la figure.
- 😀 L'exemple de la vidéo porte sur la construction de l'image du triangle ABC par la translation définie par le vecteur M/N.
- 😀 Pour chaque point du triangle, on construit une droite parallèle à la direction du vecteur et on reporte la longueur du vecteur.
- 😀 L'image du point A est obtenue en construisant une droite parallèle au vecteur M/N passant par A, puis en reportant la longueur du vecteur.
- 😀 De même, pour les points B et C, on construit des droites parallèles à M/N passant respectivement par B et C, puis on reporte la longueur du vecteur.
- 😀 Les images des points A, B et C sont appelées A', B' et C' après translation.
- 😀 Une fois les images des points obtenues, on relie les nouveaux points (A', B', C') pour obtenir l'image du triangle ABC.
- 😀 Le triangle image est exactement le même triangle que l'original, simplement déplacé dans la direction du vecteur, sans rotation ni symétrie.
Q & A
Qu'est-ce qu'une translation en géométrie ?
-Une translation est un mouvement où une figure est glissée dans une direction donnée sur une distance précise. La direction est définie par un vecteur et la longueur du glissement est la distance du vecteur.
Qu'est-ce qu'un vecteur et comment est-il utilisé dans cette vidéo ?
-Un vecteur est un objet mathématique qui représente la direction et la longueur du glissement dans une translation. Dans la vidéo, le vecteur est défini par la flèche qui va du point M au point N.
Pourquoi la direction de la translation est donnée par la flèche MN ?
-La direction de la translation est donnée par la flèche MN, car elle montre la direction du glissement. Le sens de la flèche (de M vers N) indique dans quel sens la figure sera déplacée.
Quelle est l'importance de la longueur de la flèche dans une translation ?
-La longueur de la flèche détermine la distance du glissement. Elle indique de combien la figure sera déplacée dans la direction spécifiée par le vecteur.
Que faut-il faire pour construire l'image d'un point par une translation ?
-Pour construire l'image d'un point, il faut tracer une droite parallèle au vecteur de translation passant par ce point, puis reporter la longueur du vecteur à partir de ce point dans la direction du vecteur.
Comment construire l'image du point A par la translation définie par M et N ?
-Il faut construire une droite parallèle à MN passant par le point A, puis reporter la longueur de MN à partir de A dans la direction de la flèche. Le point obtenu est l'image de A, notée A prime.
Quel est le rôle de la droite parallèle à MN dans le processus de translation ?
-La droite parallèle à MN sert à guider la direction du déplacement du point. Elle permet de maintenir la translation dans la même direction que le vecteur MN.
Comment les images des autres points (B et C) sont-elles obtenues ?
-Les images des points B et C sont obtenues de la même manière que pour le point A : on construit une parallèle à MN passant par B et C, puis on reporte la longueur de MN à partir de ces points dans la direction de la flèche.
Que se passe-t-il une fois que les images des trois points A, B, et C sont obtenues ?
-Une fois les images des trois points A, B, et C obtenues, il suffit de relier ces points pour obtenir l'image complète du triangle par la translation.
Quelles sont les caractéristiques du triangle après la translation ?
-Après la translation, le triangle conserve sa forme et sa taille, mais il est déplacé dans l'espace. Il n'y a pas de rotation ni de symétrie, seulement un glissement du triangle dans la direction et la distance définies par le vecteur MN.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Représenter un partage à l'aide d'une fraction - Sixième
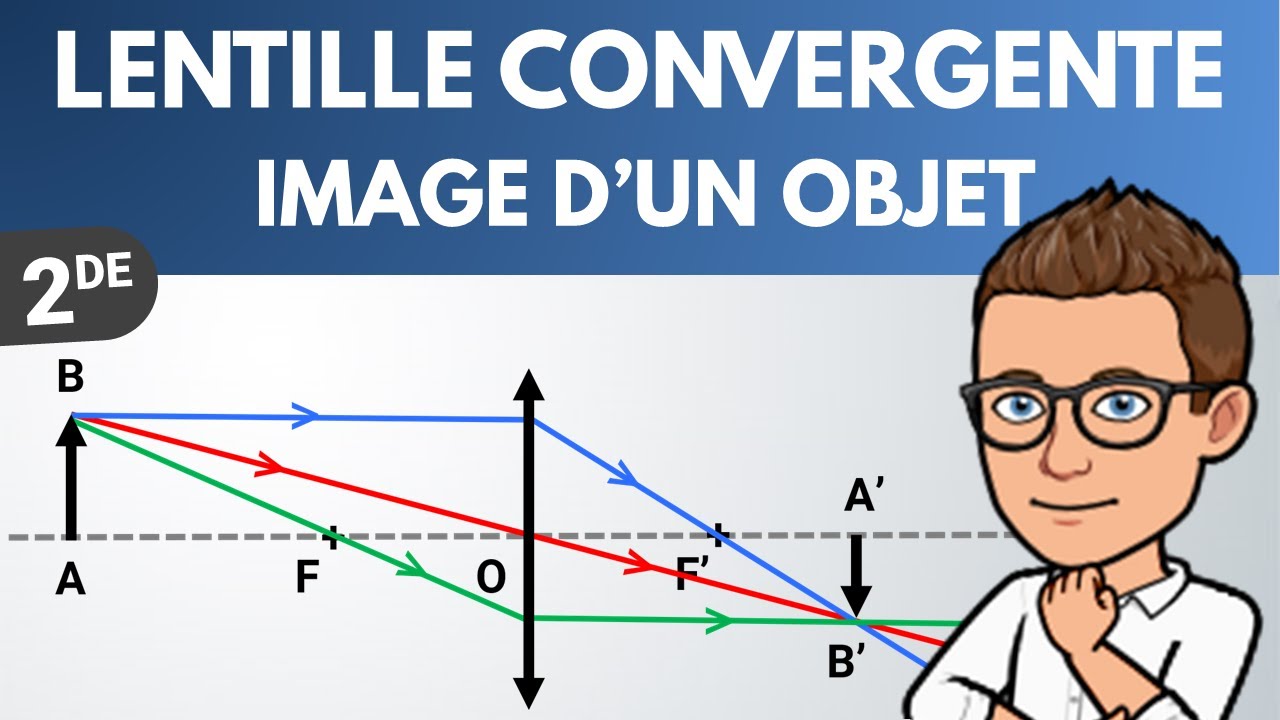
Construction de l'image d'un objet par une lentille | Seconde | Physique-Chimie

il periodo ipotetico della realtà (1° grado) | Learn Italian with Lucrezia

Pourcentage : Augmentation/diminution

Appliquer un POURCENTAGE (1) - Cinquième

Comment maitriser sa vectorisation dans Illustrator avec Photoshop [tuto Illustrator]
5.0 / 5 (0 votes)
