Variance and Standard Deviation for Grouped Data
Summary
TLDRIn this video, the presenter explains how to calculate variance and standard deviation for grouped data, building on previously defined concepts for ungrouped data. The video details the relevant formulas, emphasizing the importance of frequency and class marks. A step-by-step example illustrates how to compute squared class marks, the sum of frequencies, and necessary components for the variance formula. The calculations are clearly demonstrated, culminating in the determination of variance and standard deviation. Viewers are encouraged to ensure accuracy in their computations to avoid errors in the final results.
Takeaways
- 😀 The definition of variance remains the same for both ungrouped and grouped data, represented by σ² for population and s² for samples.
- 😀 Variance is calculated as the average of the squared distances of each datum from the mean.
- 😀 In group data, a different formula is used that involves frequency (f) and class marks (x).
- 😀 The steps for calculating variance in grouped data include squaring class marks, multiplying by frequency, and summing the results.
- 😀 Standard deviation is the positive square root of variance and indicates how closely data points cluster around the mean.
- 😀 For variance calculation in grouped data, the formula requires the summation of f times x² and f times x.
- 😀 Each class mark's squared value must be computed to facilitate variance calculation.
- 😀 The calculation of the total number of data points (n) is crucial for both variance and standard deviation formulas.
- 😀 Precision in calculations is essential, as errors in any number will affect the final variance and standard deviation results.
- 😀 The example provided demonstrates a step-by-step calculation of variance and standard deviation using a frequency distribution table.
Q & A
What is the definition of variance in the context of grouped data?
-Variance in grouped data is still defined as the average of the squared distances of each datum from the mean. The notation used is σ² for the population and s² for the sample.
How does the formula for variance differ between grouped and ungrouped data?
-While the concept of variance remains the same, the formula for grouped data requires additional steps to account for frequencies and class marks, whereas ungrouped data uses individual data points directly.
What do the symbols Σ, f, x, and n represent in the variance formula?
-In the variance formula, Σ represents summation (addition), f is the frequency of each class, x is the class mark, and n is the total number of data points in the set.
What is the first step in calculating the variance for grouped data?
-The first step is to square each of the class marks, which will be used in subsequent calculations.
What is the purpose of multiplying frequency (f) by class marks (x)?
-Multiplying frequency by class marks allows us to find the weighted contribution of each class mark to the overall dataset, which is necessary for calculating variance.
What is the significance of the denominator in the variance formula?
-The denominator, which is n times (n-1), accounts for the total number of data points and adjusts for the degrees of freedom, ensuring the variance estimate is unbiased.
How is standard deviation calculated from variance?
-Standard deviation is calculated as the positive square root of the variance, providing a measure of dispersion in the same units as the original data.
What happens if a calculation error occurs in the variance computation?
-A calculation error in any of the steps can significantly affect the final results for variance and standard deviation, leading to incorrect interpretations of the data.
Why is it important to round the final results for variance and standard deviation?
-Rounding the final results ensures clarity and precision in reporting, particularly when presenting the findings in a practical context.
What values are required to calculate variance in the provided example?
-In the example, the required values to calculate variance include the summation of f times x² (Σ(fx²)), the summation of fx (Σ(fx)), and the total number of frequencies (n).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Statistika Part. 4 | Ukuran Penyebaran, Ragam, Varian, Simpangan Rata-rata, Simpangan Baku

Statistika Bagian 7 - Simpangan Baku dan Varian Data Tunggal dan Data Berkelompok

Cara menentukan nilai varian (Ragam) dan Standar deviasi (Simpangan baku) data tunggal dan kelompok
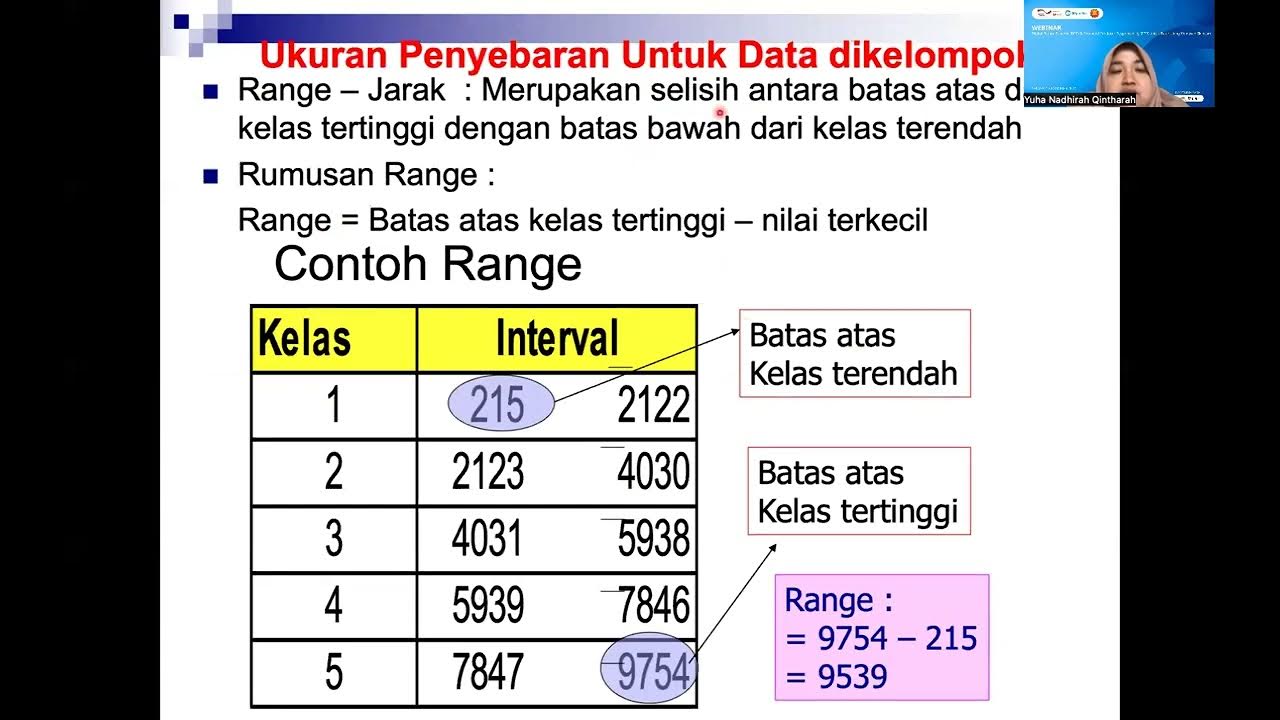
Varians dan Simpangan Baku

Simpangan rata-rata, ragam dan simpangan baku data tunggal

MEASURES OF VARIATION: RANGE, VARIANCE AND STANDARD DEVIATION FOR GROUPED DATA
5.0 / 5 (0 votes)