Factored Form of a Quadratic Equation - Nerdstudy

Summary

In this lesson, viewers learn about the factored form of quadratic equations, an alternative representation alongside vertex and standard forms. The video illustrates how a standard quadratic equation can be factored to reveal its roots, or zeros, which are key points on the graph. By analyzing the equation, the video explains how the roots correspond to x-values where y equals zero, helping to visualize the parabola's shape. The presenter highlights the significance of the coefficient 'a' in determining the graph's orientation, concluding that the factored form aids in predicting graph behavior, although it doesn't provide complete details about its width or vertex position.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

What is the factored form of a quadratic equation?

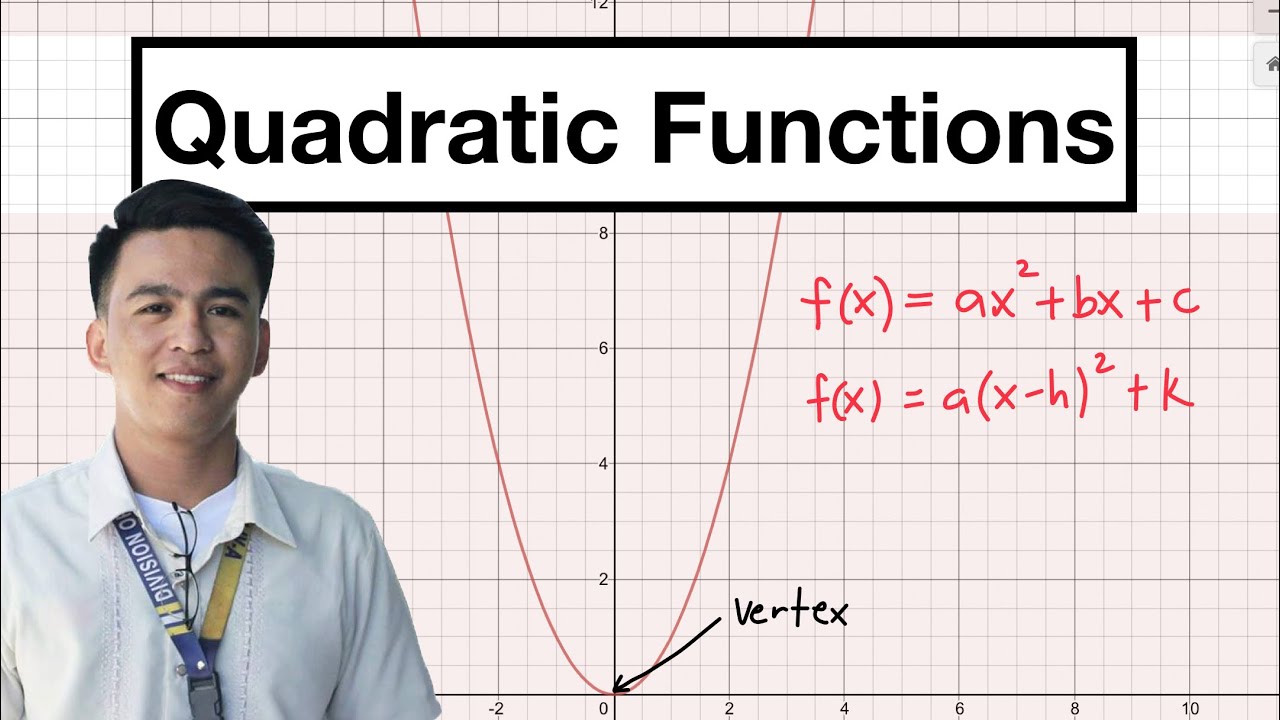
The factored form of a quadratic equation expresses it as a product of two binomials, such as y = (x - r1)(x - r2), where r1 and r2 are the roots of the equation.

How does the factored form relate to the standard form of a quadratic equation?

The factored form can be derived from the standard form of a quadratic equation, ax^2 + bx + c, by factoring it to find its roots, which are the values of x that make y equal to zero.

What are the roots of the equation given in the script?

For the equation y = (x - 4)(x + 3), the roots are x = 4 and x = -3.

What happens to the value of y when x equals one of the roots?

When x equals one of the roots, the corresponding factor becomes zero, resulting in y being equal to zero, which identifies points on the graph where the parabola intersects the x-axis.

What does the variable 'a' indicate in the context of a quadratic equation?

The variable 'a' indicates the direction of the parabola: if a is positive, the graph opens upwards, indicating a minimum vertex; if a is negative, it opens downwards, indicating a maximum vertex.

Why is it important to understand the factored form of a quadratic equation?

Understanding the factored form helps in easily identifying the zeros of the function and provides insights into the shape and orientation of the graph.

How can we visually represent the quadratic equation derived from its factored form?

By plotting the roots on a graph, we can mark points where y = 0, and using the value of 'a' to determine the direction of the parabola, we can sketch the graph accordingly.

What does it mean when the graph of a quadratic equation has a minimum vertex?

A minimum vertex indicates the lowest point on the graph, which occurs when the parabola opens upwards, and it represents the smallest y-value of the function.

How can one find the width of the parabola from the factored form?

The width of the parabola is not determined by the factored form alone; additional information, such as the value of 'a', is needed to assess whether the parabola is wide or narrow.

What should one do if they don't understand how to factor a quadratic equation?

If you're unsure how to factor a quadratic equation, it is recommended to watch a video specifically focused on factoring quadratic equations before attempting to understand the factored form.