FUNGSI KUADRAT

Summary

This educational lesson explains the concept of quadratic functions, including their general form, graph, and properties. The instructor covers key topics such as the vertex form of quadratic equations, how the graph behaves based on the value of 'a', and the discriminant's role in determining the number of intersections with the x-axis. The lesson also walks through solving quadratic equations using three points or the vertex. Practice problems help solidify understanding, including real-world applications. The session concludes with a motivational message emphasizing perseverance and effort in learning.

Takeaways

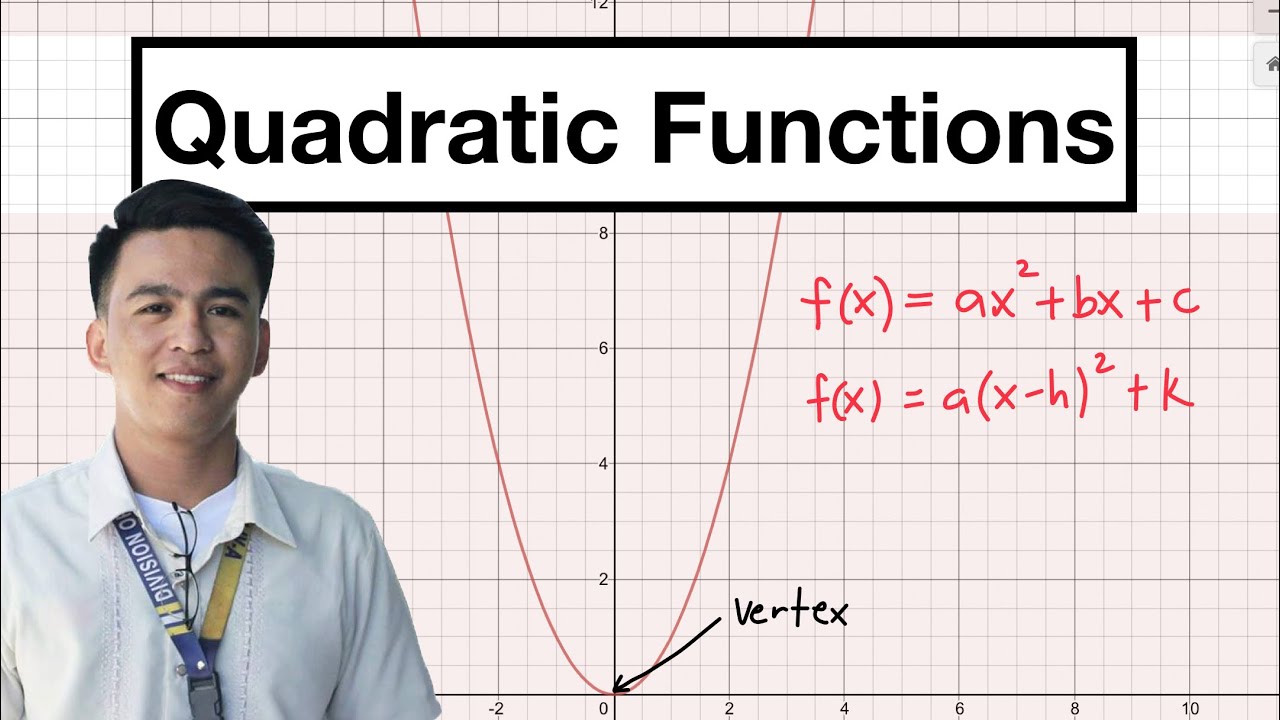
• 😀 Quadratic functions have the general form: y = ax^2 + bx + c, where a ≠ 0.
• 😀 The graph of a quadratic function is a parabola, which can open upwards or downwards depending on the value of 'a'.
• 😀 If a > 0, the parabola opens upwards, creating a minimum point. If a < 0, the parabola opens downwards, creating a maximum point.
• 😀 The axis of symmetry of a parabola is given by the equation: x = -b / 2a.
• 😀 The vertex of the parabola is at the point (-b / 2a, f(-b / 2a)).
• 😀 The discriminant (D = b² - 4ac) helps determine the number of real roots (x-intercepts) of a quadratic function: - D > 0: Two real roots (two x-intercepts), - D = 0: One real root (one x-intercept), - D < 0: No real roots (no x-intercepts).
• 😀 A quadratic equation can be written in factored form: y = a(x - x₁)(x - x₂), where x₁ and x₂ are the roots.
• 😀 The equation of a parabola can also be written using its vertex form: y = a(x - p)² + q, where (p, q) is the vertex.
• 😀 If a parabola passes through three points, the quadratic equation can be solved by substituting the coordinates of the points into the general form y = ax² + bx + c.
• 😀 In practical problems, you can use the quadratic function to determine properties like maximum area or points of intersection, such as in the case of a rectangular plot with a fixed perimeter.
• 😀 The learning process requires perseverance and effort to master concepts like quadratic functions, and success will follow with consistent effort.

Q & A

What is the general form of a quadratic function?

The general form of a quadratic function is y = AX^2 + BX + C, where A is not equal to zero and A, B, and C are constants.

What type of graph does a quadratic function represent?

A quadratic function represents a parabola-shaped graph.

What is the axis of symmetry for a quadratic function?

The axis of symmetry for a quadratic function is given by the equation x = -B/2A.

What does the value of A in the quadratic function determine?

The value of A determines the direction in which the parabola opens. If A is positive, the parabola opens upwards; if A is negative, the parabola opens downwards.

How do you find the vertex of a parabola?

The vertex of the parabola can be found using the formula x = -B/2A for the x-coordinate, and substituting this value back into the quadratic function to find the y-coordinate.

What happens if the discriminant (D) of a quadratic function is greater than 0?

If the discriminant (D) is greater than 0, the quadratic equation has two real and distinct roots, meaning the parabola intersects the x-axis at two points.

What happens if the discriminant (D) of a quadratic function is equal to 0?

If the discriminant (D) is equal to 0, the quadratic equation has exactly one real root, meaning the parabola touches the x-axis at only one point.

What happens if the discriminant (D) of a quadratic function is less than 0?

If the discriminant (D) is less than 0, the quadratic equation has no real roots, meaning the parabola does not intersect the x-axis.

How do you write the quadratic function if the parabola passes through three arbitrary points?

If the parabola passes through three arbitrary points, the quadratic function can be written as y = AX^2 + BX + C, and the system of equations formed by substituting the points can be solved to find A, B, and C.

How do you find the quadratic function when the parabola passes through a point and its vertex is known?

The quadratic function can be written as y = A(X - P)^2 + Q, where P and Q are the coordinates of the vertex, and the value of A can be found by substituting a known point into the equation and solving for A.