Fungsi Kuadrat Bagian 1 - Matematika Wajib Kelas X m4thlab
Summary
TLDRIn this educational video on quadratic functions, the presenter explains the basics, including the standard form of quadratic equations, their graphs, and key properties. The video covers how to identify the intersection points with the x-axis and y-axis, how to determine the vertex (extreme point), and the significance of the discriminant. Through practical examples, viewers learn how to find the coordinates of the vertex, the axis of symmetry, and the maximum or minimum values of quadratic functions. This foundational lesson is essential for students preparing for university entrance exams, with future videos delving deeper into graphing techniques.
Takeaways
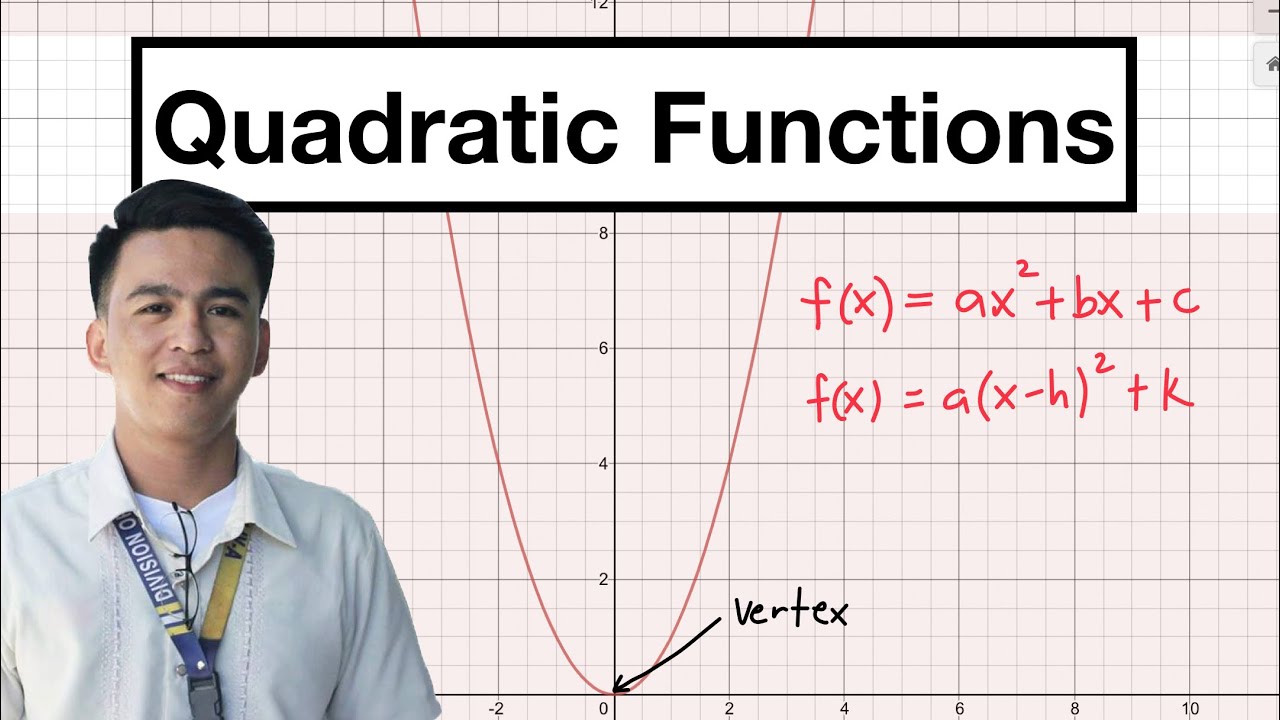
- 😀 Quadratic functions have the general form: f(x) = ax² + bx + c, where 'a' is not equal to zero. This form determines the shape and properties of the graph.
- 😀 The graph of a quadratic function is called a parabola, and it can either open upwards or downwards depending on the sign of the 'a' coefficient.
- 😀 If 'a' is positive, the parabola opens upwards, indicating a minimum value. If 'a' is negative, the parabola opens downwards, indicating a maximum value.
- 😀 To find the x-intercepts of a quadratic function, set f(x) to 0 and solve for x. These are the points where the graph intersects the x-axis.
- 😀 To find the y-intercept of a quadratic function, substitute x = 0 into the equation, which will give the value of f(0) or the constant 'c'.
- 😀 The vertex of a quadratic function (also called the turning point or extremum) can be found using the formula x = -b / 2a for the x-coordinate, and then substitute this into the function to find the y-coordinate.
- 😀 The axis of symmetry of the parabola passes through the vertex and is given by the equation x = -b / 2a.
- 😀 The discriminant (Δ) of a quadratic equation, Δ = b² - 4ac, can help determine the nature of the roots. If Δ > 0, there are two distinct real roots. If Δ = 0, there is one real root (the vertex touches the x-axis). If Δ < 0, there are no real roots.
- 😀 For quadratic functions in the form f(x) = ax² + bx + c, the maximum or minimum value occurs at the vertex, with the value of y at the vertex given by the formula y = -Δ / 4a.
- 😀 When working with quadratic functions, understanding the graph’s orientation, intercepts, vertex, and axis of symmetry is key to fully analyzing its behavior and solving related problems.
- 😀 A quadratic equation can be factored or solved using methods such as the quadratic formula, completing the square, or graphing to find its roots and other key characteristics.
Q & A
What is a quadratic function?
-A quadratic function is a type of polynomial function that has a degree of 2. Its general form is fx = ax^2 + bx + c, where 'a', 'b', and 'c' are constants and 'a' is not equal to zero.
What is the significance of the coefficients a, b, and c in a quadratic function?
-In the quadratic function fx = ax^2 + bx + c, 'a' is the coefficient of x^2, 'b' is the coefficient of x, and 'c' is the constant term. The values of 'a', 'b', and 'c' determine the shape and position of the parabola.
How can you determine if the graph of a quadratic function opens upwards or downwards?
-The direction of the parabola depends on the value of 'a'. If 'a' is positive, the parabola opens upwards. If 'a' is negative, the parabola opens downwards.
What is the discriminant, and how is it used in quadratic functions?
-The discriminant, denoted as 'D', is calculated using the formula D = b^2 - 4ac. It helps determine the nature of the roots of the quadratic equation. If D > 0, the equation has two real roots; if D = 0, there is one real root; and if D < 0, there are no real roots.
How do you find the x-intercepts (or roots) of a quadratic function?
-To find the x-intercepts of a quadratic function, set fx = 0 and solve the resulting quadratic equation. This can be done by factoring, completing the square, or using the quadratic formula.
What is the vertex of a parabola, and how is it calculated?
-The vertex is the highest or lowest point of the parabola, depending on whether it opens upwards or downwards. The x-coordinate of the vertex (also called the axis of symmetry) can be calculated using the formula x = -b / 2a. The y-coordinate of the vertex can be found by substituting the x-coordinate into the original quadratic equation.
What is the axis of symmetry of a quadratic function?
-The axis of symmetry is a vertical line that passes through the vertex of the parabola. Its equation is given by x = -b / 2a, where 'b' and 'a' are the coefficients from the quadratic equation.
How can you find the y-intercept of a quadratic function?
-The y-intercept of a quadratic function is the point where the graph crosses the y-axis. To find it, set x = 0 and solve for f(0). The value of f(0) is the y-intercept.
What does the term 'maximum' or 'minimum' refer to in a quadratic function?
-The 'maximum' or 'minimum' refers to the y-value of the vertex. If the parabola opens upwards, the vertex represents a minimum value. If the parabola opens downwards, the vertex represents a maximum value.
What is the relationship between a quadratic function and its graph?
-The graph of a quadratic function is a parabola. It represents the set of all points (x, fx) that satisfy the quadratic equation. The shape and position of the parabola are determined by the values of the coefficients 'a', 'b', and 'c'.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade Now5.0 / 5 (0 votes)