On Fibonacci Sequence (GEC 104- Math in the Modern world)
Summary
TLDRThe video discusses the Fibonacci sequence, a series of numbers where each number is the sum of the two preceding ones, originating from Fibonacci's study of rabbit populations. It highlights the sequence's presence in nature, such as in plants, pinecones, and sunflowers, and its applications in various fields like science, cryptography, and engineering. The video also introduces 'fib' poems, which use the Fibonacci sequence as a structure for syllable counts, blending mathematics and poetry. Additionally, it explores the Fibonacci spiral and its connection to natural patterns and mathematical properties.
Takeaways
- 🐇 The Fibonacci sequence was first observed by Fibonacci while investigating rabbit breeding under ideal conditions.
- 📊 The sequence begins with 1, 1, 2, 3, 5, 8, and follows the rule that each number is the sum of the two preceding ones.
- 🇮🇹 It is named after the Italian mathematician Leonardo Pisano Fibonacci, born in Pisa.
- 🌻 Fibonacci numbers appear in nature, such as in the arrangement of sunflower seeds, spirals in pine cones, and the number of petals in flowers.
- 🍍 The Fibonacci sequence is found in the spiral patterns of pineapples, with numbers like 5 and 8, or 8 and 13.
- 📐 Fibonacci numbers have interesting mathematical properties, including relationships with sums, differences, and the golden ratio (1.618).
- 🔑 The sequence is applied in cryptography, such as securing communications using Fibonacci numbers.
- 🤖 Students built a robot programmed with Fibonacci numbers, using simple algebraic equations to represent the sequence.
- 🏗️ The Fibonacci sequence has practical applications in engineering, finance, data structures, and algorithms.
- 📜 A 'Fib' is a type of poem where the number of syllables per line follows the Fibonacci sequence, typically with 6 lines and a total of 20 syllables.
Q & A
What is the Fibonacci sequence?
-The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. It starts with 0, 1, and continues as 1, 2, 3, 5, 8, and so on.
How did Fibonacci first observe the sequence?
-Fibonacci first observed the sequence while studying how fast rabbits could breed under ideal circumstances, using a population model that tracked rabbit pairs over time.
What is the population of rabbits after the seventh month in Fibonacci's model?
-In the seventh month, the population would be 13 pairs of rabbits, following the Fibonacci sequence.
Why is the sequence called the Fibonacci sequence?
-It is named after Leonardo Fibonacci (Leonardo Pisano Bigollo), an Italian mathematician who popularized the sequence in Western Europe, although its origins date back to Indian mathematicians.
How is the Fibonacci sequence represented in nature?
-The Fibonacci sequence appears in nature in various ways, such as the arrangement of seeds in sunflowers, the spirals of pinecones and pineapples, and the number of petals on certain flowers.
What is the connection between Fibonacci numbers and the golden ratio?
-As the Fibonacci numbers increase, the ratio of consecutive Fibonacci numbers approaches the golden ratio, which is approximately 1.618.
Can you give an example of a flower with Fibonacci-numbered petals?
-Yes, examples include lilies with 1 petal, Euphorbia with 2 petals, Columbine with 5 petals, and Shasta daisies with 21 petals.
What applications of the Fibonacci sequence are found in modern technology?
-The Fibonacci sequence is used in fields like cryptography, computer algorithms, financial engineering, audio compression, and robotic programming.
What is a Fibonacci poem, and how is it structured?
-A Fibonacci poem, or 'fib,' is a six-line poem where the syllable count of each line follows the Fibonacci sequence: 1, 1, 2, 3, 5, 8 syllables, respectively.
How are Fibonacci numbers connected to Pythagorean triples?
-Any four consecutive Fibonacci numbers can be combined to form a Pythagorean triple, which is a set of three integers that satisfy the Pythagorean theorem.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video
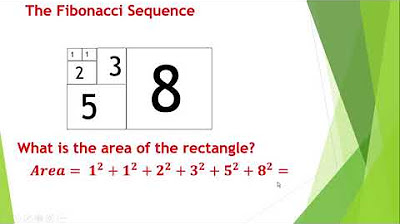
Fibonacci Sequence

Unit 1 | Lesson 3: The Fibonacci Sequence (Mathematics in the Modern World)

THE FIBONACCI SEQUENCE AND THE GOLDEN RATIO || MATHEMATICS IN THE MODERN WORLD

What is the Fibonacci Sequence?

The Fibonacci Sequence and Rabbits with Math Dude, Jason Marshall

EMODULE 1.2 - The Fibonacci Sequence
5.0 / 5 (0 votes)