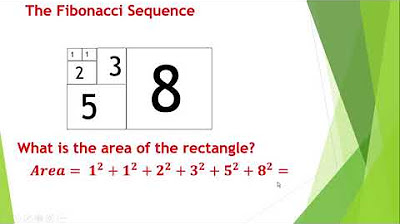THE FIBONACCI SEQUENCE AND THE GOLDEN RATIO || MATHEMATICS IN THE MODERN WORLD

Summary

This video script explores the Fibonacci sequence, a series of numbers where each term is the sum of the two preceding ones, starting from one. Leonardo of Pisa, known as Fibonacci, introduced the sequence through a rabbit reproduction problem. The script delves into the sequence's prevalence in nature, such as in the spiral patterns of sunflowers and pinecones, and its relation to the golden ratio, approximately 1.618. It also demonstrates how to calculate terms in the sequence, concluding with an example to find the 15th term, which is 610.

Takeaways

• 📚 Lesson One focused on nature and patterns, while Lesson Two introduced the Fibonacci sequence.
• 🔢 Leonardo Pisano, known as Fibonacci, was a prominent European mathematician of the Middle Ages, credited with introducing the Arabic numeral system to Europe.
• 🐰 The Fibonacci sequence was discovered through an investigation into the reproduction of rabbits, where each new pair of rabbits produces another pair.
• 🌱 The sequence starts with two ones and each subsequent number is the sum of the two preceding ones, forming a pattern like 1, 1, 2, 3, 5, 8, 13, and so on.
• 📈 The Fibonacci sequence can be used to predict the number of rabbit pairs after a given number of months, with 144 pairs after one year in the example provided.
• 🌻 The Fibonacci sequence is observed in nature, such as the spiral structure of sunflowers and the arrangement of pinecones.
• 🌺 The number of petals in many flowers is often a Fibonacci number, and this can also be seen in the structure of fruits like pineapples.
• 🎨 The golden ratio, approximately 1.618, is closely related to the Fibonacci sequence and is often found in art and architecture, including the Mona Lisa.
• 🔍 The golden ratio can be expressed using the formula \( a \over b = (a + b) \over a \), where \( a \) and \( b \) are consecutive Fibonacci numbers.
• 📝 To find a specific term in the Fibonacci sequence, you start with the first two terms as one and continue by adding the last two terms to get the next one.
• 👋 The video concludes by encouraging viewers to like, subscribe, and hit the bell for more educational content.

Q & A

Who is Leonardo Pisano, also known as Fibonacci?

Leonardo Pisano, nicknamed Fibonacci, was the greatest European mathematician of the Middle Ages, born in 1170 and died in 1240. He is known for introducing the Arabic number system to Europe.

What is the origin of the Fibonacci sequence?

The Fibonacci sequence was discovered after an investigation on the reproduction of rabbits. It represents the number of rabbit pairs in a field over a period of time, assuming a constant rate of reproduction.

How is the Fibonacci sequence defined mathematically?

The Fibonacci sequence is an infinite series of numbers where each number after the first two is the sum of the two preceding ones. It starts with 1, 1, and then follows with 2, 3, 5, 8, 13, and so on.

What is the significance of the Fibonacci sequence in nature?

The Fibonacci sequence is observed in nature in various forms, such as the spiral structure of sunflowers and pine cones, the arrangement of petals in flowers, and the pattern of pineapple crowns.

How many rabbit pairs would there be at the end of one year according to the Fibonacci sequence?

According to the script's illustration, there would be 144 pairs of rabbits at the end of one year if the sequence follows the Fibonacci pattern.

What is the golden ratio and how is it related to the Fibonacci sequence?

The golden ratio, often denoted by the Greek letter phi (φ), is approximately equal to 1.618. It is related to the Fibonacci sequence as the ratio between successive Fibonacci numbers converges to the golden ratio.

Can the golden ratio be found in art and architecture?

Yes, the golden ratio is often found in art and architecture, believed to provide aesthetically pleasing proportions, such as in the structure of the Mona Lisa.

How can one find the 9th term of the Fibonacci sequence?

To find the 9th term of the Fibonacci sequence, start with the first two terms as 1 and 1, then continue adding the last two terms to get the next term, resulting in 34 as the 9th term.

What is the 15th term of the Fibonacci sequence?

Following the pattern of the Fibonacci sequence, the 15th term is 610.

Do plants perform mathematical calculations?

Plants do not perform mathematical calculations, but their growth patterns often follow the Fibonacci sequence, which is a result of natural processes.

Outlines

00:00

📚 Introduction to Fibonacci Sequence and Nature

The script begins with an introduction to the Fibonacci sequence, named after Leonardo Pisano Bigollo, known as Fibonacci. He was a prominent European mathematician from the Middle Ages who introduced the Arabic numeral system to Europe. The sequence, which is an infinite series of numbers starting with 1 and 1, follows a pattern where each number is the sum of the two preceding ones. The script also delves into the origin of the sequence, which was inspired by the hypothetical scenario of rabbit reproduction. It further explains how the Fibonacci sequence appears in nature, particularly in the spiral patterns found in sunflowers and pine cones, illustrating the prevalence of this mathematical concept in natural phenomena.

05:01

🌼 Fibonacci Sequence in Nature and the Golden Ratio

This paragraph explores the presence of the Fibonacci sequence in various aspects of nature, such as the arrangement of petals in flowers and the structure of fruits like pineapples. It emphasizes that while plants do not perform mathematics, their growth patterns often follow the Fibonacci sequence. The script introduces the concept of the golden ratio, denoted by the Greek letter phi (φ), which is approximately 1.618. This ratio is derived from the Fibonacci sequence and is found in various natural structures. The golden ratio is also related to the Fibonacci sequence through a specific formula. The script concludes with an example of how to calculate the ninth and fifteenth terms of the Fibonacci sequence, demonstrating the application of the sequence in mathematical problems.

Keywords

💡Fibonacci Sequence

The Fibonacci Sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 0 and 1. It is central to the video's theme as it is the main subject being discussed. The script uses the sequence to illustrate patterns in nature, such as in the arrangement of rabbit populations and the spiral patterns found in sunflowers and pinecones.

💡Leonardo Pisano Bigollo

Leonardo Pisano Bigollo, known as Fibonacci, is a medieval Italian mathematician who introduced the sequence that now bears his nickname. He is mentioned in the script as the greatest European mathematician of the Middle Ages, having introduced the Arabic numeral system to Europe and being the discoverer of the sequence through his investigation on rabbit reproduction.

💡Nature

Nature is a key context in the video, as it demonstrates the prevalence of the Fibonacci Sequence in natural phenomena. The script provides examples of how the sequence appears in the arrangement of leaves, the spirals of sunflowers, and the structure of pinecones, illustrating the mathematical patterns inherent in organic growth.

💡Golden Ratio

The Golden Ratio is a mathematical concept closely related to the Fibonacci Sequence, often denoted by the Greek letter phi (Φ) and approximately equal to 1.618. It is a ratio that appears in various aspects of art, architecture, and nature, and the script explains how it can be derived from the sequence, emphasizing its prevalence in natural structures.

💡Rabbit Reproduction

Rabbit Reproduction is used in the script as a metaphorical example to explain the Fibonacci Sequence. It describes a scenario where a pair of rabbits can reproduce and the population grows according to the sequence's pattern, serving as a practical illustration of how the sequence can model real-world phenomena.

💡Sunflower

The Sunflower is an example of how the Fibonacci Sequence manifests in nature. The script describes the spiral structure of a sunflower, which follows the Fibonacci Sequence in the arrangement of its seeds, showcasing the sequence's relevance in botanical patterns.

💡Pine Cone

Pine Cones, like sunflowers, exhibit the Fibonacci Sequence in their spiral structure. The script points out that the arrangement of scales on a pine cone follows the sequence, further emphasizing the natural occurrence of this mathematical pattern.

💡Flower Petals

The number of petals on a flower is mentioned in the script as often being a Fibonacci number, such as 3, 5, 8, etc. This illustrates how the sequence can be observed in the symmetry and structure of flowers, adding to the theme of mathematical patterns in nature.

💡Pineapple

The Pineapple is cited in the script as another example of the Fibonacci Sequence in nature, specifically in the pattern of its crown and the arrangement of its fruit scales, which follow the sequence's pattern, reinforcing the video's theme of mathematical patterns in organic structures.

💡Arithmetic Progression

Although not explicitly labeled as such in the script, the concept of adding the last two terms to get the next term in the Fibonacci Sequence is an example of an arithmetic progression. This is a fundamental aspect of the sequence and is essential to understanding how it grows and develops.

💡Pattern Recognition

Pattern Recognition is an underlying theme in the video, as it discusses how the Fibonacci Sequence can be identified in various natural settings. The script encourages viewers to observe and recognize these patterns in the world around them, highlighting the interconnectedness of mathematics and nature.

Highlights

Lesson one focused on nature and patterns, while lesson two introduced the Fibonacci sequence.

Leonardo Pisano, known as Fibonacci, was a prominent European mathematician of the Middle Ages.

Fibonacci's contributions include introducing the Arabic numeral system to Europe.

The Fibonacci sequence was discovered through an investigation of rabbit reproduction.

The sequence starts with two ones and each subsequent term is the sum of the two preceding ones.

An example calculation shows that 144 pairs of rabbits would be present after one year.

The Fibonacci sequence is observed in nature, such as in the spiral structure of sunflowers.

Pine cones also exhibit the Fibonacci spiral, demonstrating its prevalence in nature.

The number of petals in flowers and the arrangement of seeds in pineapples often relate to Fibonacci numbers.

Plants do not 'do math' but their growth patterns follow the Fibonacci sequence.

The golden ratio, approximately 1.618, is closely related to the Fibonacci sequence.

The golden ratio can be expressed as a ratio between two numbers, following a specific formula.

The golden ratio is observed in various natural structures, such as the Mona Lisa's composition.

A method to find a specific term in the Fibonacci sequence is demonstrated using the ninth term as an example.

The 15th term of the Fibonacci sequence is calculated as 610 in the lesson.

The video encourages viewers to like, subscribe, and hit the bell for more educational content.

Transcripts

last discussion our lesson one

all about nature and pattern in lesson

two we will discuss

the fibonacci sequence

who is leonardo obisa

fibonacci okay by the way

ansaritang fibonacci is a nickname

leonardo so fibonacci is the greatest

european mathematician of the middle

ages

he was born in 1170 and died in 1240.

he introduced the arabic number system

in europe

okay let's discuss the origin

of fibonacci sequence

okay s

it was a pair of rabbit fibonacci

sequence was discovered

after an investigation on the

reproduction of

rabbits

let's consider this illustration

suppose a newly born pair of rabbits

one male and one female are put in a

field

rabbits are able to mate at the age of

one month

so that at the end of the second month a

female can produce

another pair of rabbits consider this as

a one male and one female of rabbit

okay so nagma matured sila

in a month after that they can produce

another pair

of rabbits so get another one scenario

sequence okay

fibonacci sequence is an integer in the

infinite sequence

1 1 2 3

five eight thirteen so ethiopian

patterns are number of players no

uh rabbit reproduction of which the

first two terms

are one and one and

its succeeding term is the sum of the

two

immediately preceding in short

we add the last two terms to get the

next term

okay how many pairs will be there in one

year

so gamma kyung illustration at in kanina

yamato illustration

paris after 12 months

so we have this pattern using this

pattern we have one

one two three five eight thirteen

so my kitten attend now

next term young last two terms

eight plus thirteen get twenty one so

parama young next at 21

21 plus 13 get 34. so 55

89 144 so ebig sabin

144 pairs will be there at the end of

one year so it in first second third

fourth

pip six seven eight nine ten eleven

twelve month

okay fibonacci sequence in nature paul

supa anubinati malay relates the

fibonacci sequence in nature so

or how we can relate fibonacci sequence

in nature

so pedi banati marinate

a fibonacci sequence in nature yes for

example

the sunflower okay fibonacci spiral

in sunflower no mai kita

you can try to observe the spiral

structure of the sunflower

so this is an example of fibonacci

sequence

another is the pine cone so

another is the pine cones so

you clearly show the fibonacci spiral

okay so nothing young arrangement no

but no pine cones okay so

also we can relate or we can uh

uh see fibonacci sequence in

different plants or like for example

flowers no so the number of

petals a number of petals of a flower

are often fibonacci numbers so

number of petals now pretty nothing

considers

and one two three four five six seven

eight so either number nine

petals and also

we can also relate fibonacci sequence in

fruits like the pineapple and its crown

so

and also the pineapple fruitless so

tinder not indita no it is an example of

pattern of fibonacci sequence

and here are another example of

fibonacci sequence

tanong can plants do math

no but their growth is based on this

sequence okay we can relate

uh another one class is the golden ratio

this is related on the

uh fibonacci sequence so anubian gold in

ration am

the golden ratio is often denoted by the

greek letter

pi this is approximately equal to 1.618

okay so the golden ratio can be

expressed

as the two ratio between two numbers so

you can use this

formula or this equation a over b

is equal to a plus b over a so this

illustration can be applied using this

formula

so san bernardino golden ratio in nature

so

subpainting knee mona lisa

structuring

golden ratio okay let's try to

find the indicated term of the fibonacci

sequence for example

let's find the ninth term of fibonacci

sequence so alumni

now first and second term is one okay

so that will be the c pattern

to find fibonacci sequence so therefore

i'm

nine term nut and i 34 so a nine

terminal fibonacci sequence is 34

next 15 term okay

so another input 15 term so in the

second

anatom nine terms 55 span

ten pound eleven twelve term third

thirteenth term fourteenth term at punk

ito

terms so ebxa bn and punk 15 term i 610

thank you for watching this video i hope

you learned something

don't forget to like subscribe and hit

the bell button

but updated ko for more video tutorial

this is your guide in learning your mod

lesson your walmart

channel