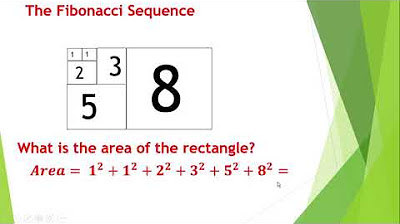What is the Fibonacci Sequence?

Summary

In this educational video, Sean Ian's from Wrath of Math explores the Fibonacci sequence, a series of numbers where each number is the sum of the two preceding ones, starting with 1 and 1. He explains the sequence's recurrence relation, F(n) = F(n-1) + F(n-2), with initial conditions F(0) = 1 and F(1) = 1. Sean demonstrates how to calculate subsequent numbers, such as the sixth Fibonacci number, which is 8, by summing the fifth and fourth numbers. The video also touches on an alternative starting point of 0, shifting the sequence. Viewers are encouraged to engage with questions and video requests.

Takeaways

• 😀 The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones.
• 📝 The sequence traditionally begins with 1, 1, and continues with 2, 3, 5, 8, 13, and so on.
• 🔢 The nth Fibonacci number (F_n) is defined by the recurrence relation F_n = F_(n-1) + F_(n-2) for n > 1.
• 💡 The sequence can also start with 0, 1, making it 0, 1, 1, 2, 3, 5, 8, and so forth.
• 📈 A recurrence relation is a mathematical process that defines a sequence by the values of its predecessors.
• 🎯 Two initial conditions are required to start the sequence: F_0 = 1 and F_1 = 1.
• 🔄 The Fibonacci sequence is a second-order recurrence relation, meaning it depends on the two preceding terms.
• 🔍 The video provides an example of calculating the sixth Fibonacci number using the recurrence relation.
• 📌 The Fibonacci sequence has applications in various fields, including mathematics, computer science, and nature.
• 👨‍🏫 The host, Sean, encourages viewers to ask questions and request topics for future videos in the comments section.

Q & A

What is the Fibonacci sequence?

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, usually starting with 1 and 1.

How is the Fibonacci sequence generated?

The Fibonacci sequence is generated by starting with 1 and 1, and then each subsequent number is the sum of the previous two numbers.

What is the recurrence relation for the Fibonacci sequence?

The recurrence relation for the Fibonacci sequence is F(n) = F(n-1) + F(n-2), where F(n) represents the nth Fibonacci number.

What are the initial conditions for the Fibonacci sequence?

The initial conditions for the Fibonacci sequence are F(0) = 1 and F(1) = 1.

Can the Fibonacci sequence start with 0?

Yes, the Fibonacci sequence can also start with 0, in which case it would look like 0, 1, 1, 2, 3, 5, and so on.

How do you find the sixth Fibonacci number using the recurrence relation?

To find the sixth Fibonacci number, you would add the fifth (5) and fourth (3) Fibonacci numbers, resulting in 8.

What is the significance of the Fibonacci sequence in mathematics?

The Fibonacci sequence is significant in mathematics as it appears in various formulas and patterns in nature, art, and architecture.

Are there any variations in how the Fibonacci sequence can be defined?

Yes, there are variations, such as starting with different initial values or using different starting points, which can result in a shifted sequence.

How does the Fibonacci sequence relate to the golden ratio?

The Fibonacci sequence is related to the golden ratio because the ratio of consecutive Fibonacci numbers approximates the golden ratio as the sequence progresses.

What is a second-order recurrence relation?

A second-order recurrence relation is one that defines a sequence where each term is a function of the two preceding terms, as seen in the Fibonacci sequence.

Can you provide an example of a Fibonacci sequence starting with 0?

An example of a Fibonacci sequence starting with 0 would be 0, 1, 1, 2, 3, 5, 8, 13, and so on.