Garis dan Sudut (5) | Hubungan Antar Sudut pada Dua Garis Sejajar | Matematika Kelas 7

Summary

In this educational video, the presenter teaches 7th-grade students about the relationships between angles formed when two parallel lines are cut by a transversal. The video covers key angle relationships including corresponding angles, vertical angles, consecutive interior angles, alternate interior angles, alternate exterior angles, and linear pairs. The presenter explains each type of angle relationship clearly, providing step-by-step instructions and examples to help students understand how to solve for unknown angles. The lesson is interactive, using diagrams to illustrate concepts, making it easy for students to follow and apply in geometry problems.

Takeaways

• 😀 Understanding the relationship between angles formed when two parallel lines are cut by a transversal is crucial in geometry.
• 😀 Vertical angles, or opposite angles, are congruent. For example, angle A1 equals angle B1, angle A2 equals angle B2, and so on.
• 😀 Adjacent angles on the same side of the transversal are supplementary, meaning their sum equals 180°.
• 😀 Same-side interior angles (angles inside the parallel lines on the same side of the transversal) add up to 180°.
• 😀 Alternate interior angles (angles on opposite sides of the transversal and inside the parallel lines) are congruent.
• 😀 Alternate exterior angles (angles on opposite sides of the transversal and outside the parallel lines) are also congruent.
• 😀 Supplementary angles on the same side of the transversal must add up to 180°.
• 😀 The sum of two same-side exterior angles equals 180°, demonstrating the importance of understanding supplementary angles.
• 😀 When solving for unknown angles, use known relationships like opposite, supplementary, and alternate angles to find the correct values.
• 😀 Practice and problem-solving with examples helps reinforce the understanding of angle relationships in parallel lines and transversals.

Q & A

What is the topic discussed in this video?

The video discusses the relationship between angles formed by two parallel lines intersected by a transversal. It covers various types of angle relationships including corresponding, alternate interior, consecutive interior, and more.

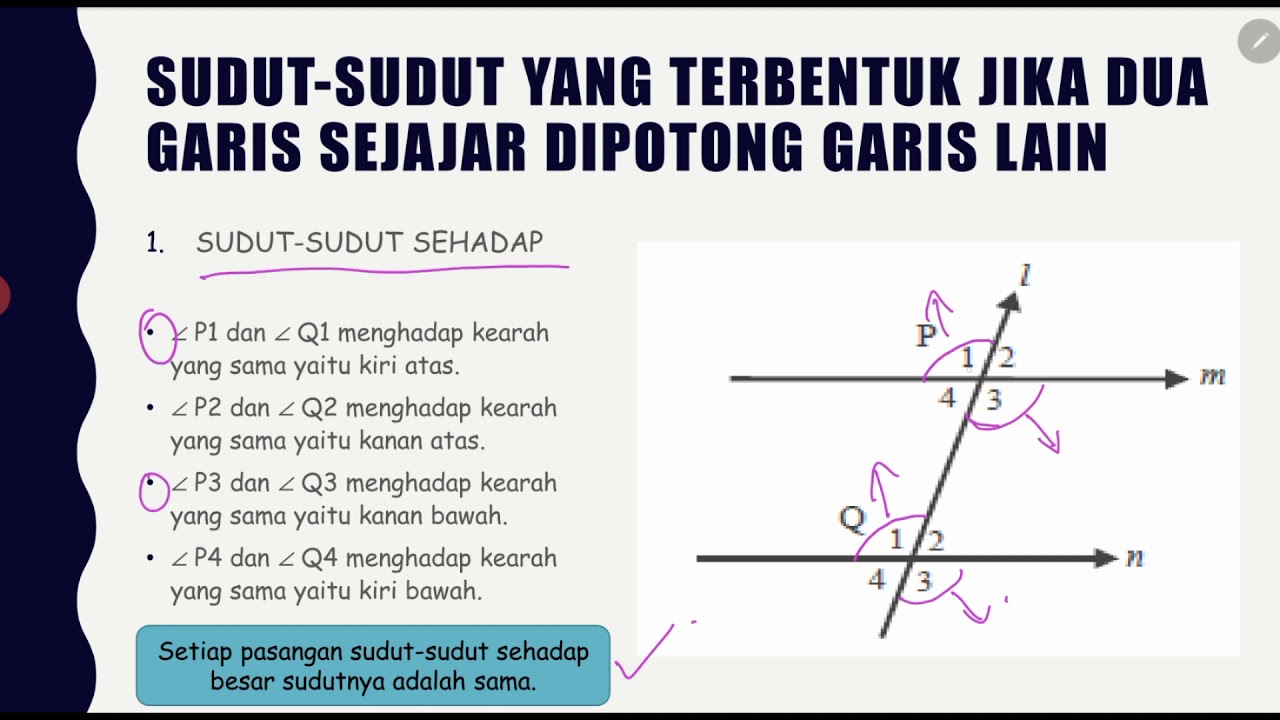
What is the relationship between corresponding angles?

Corresponding angles are angles that lie on the same side of the transversal and in corresponding positions relative to the parallel lines. These angles are equal in size.

Can you explain the concept of vertically opposite angles?

Vertically opposite angles are pairs of angles that are opposite each other when two lines intersect. These angles are always equal in size.

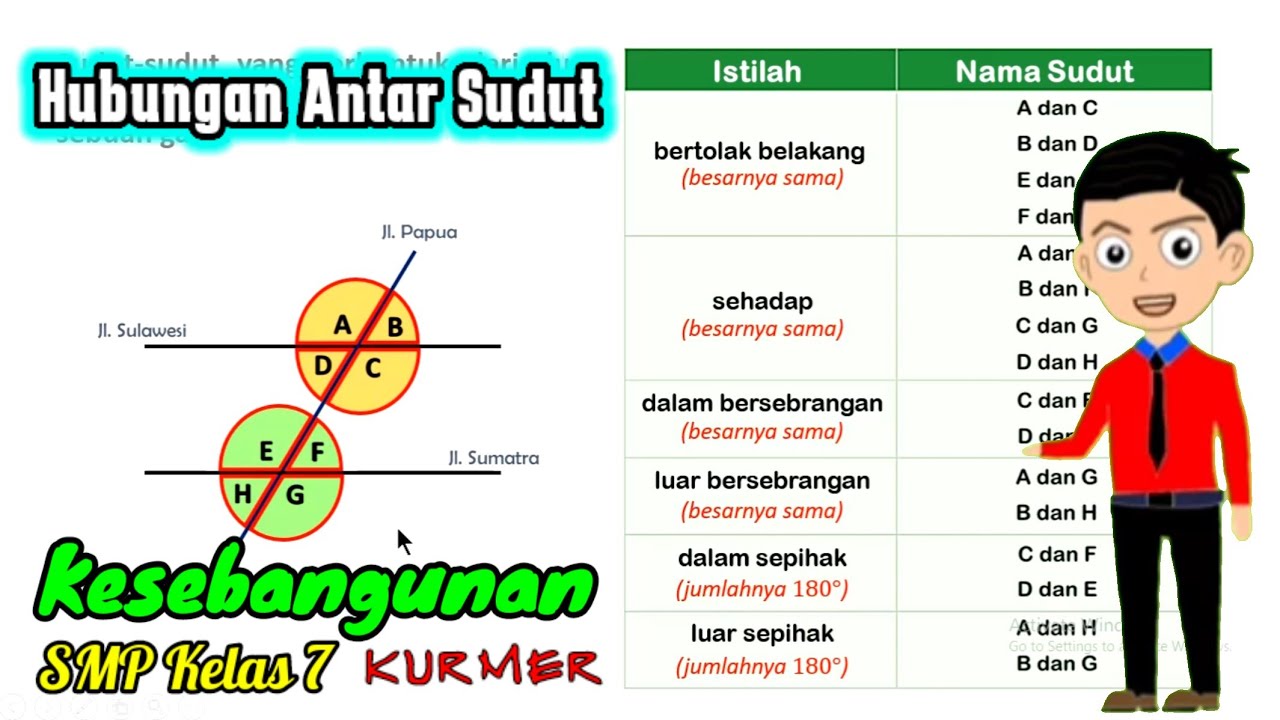
What is the sum of consecutive interior angles?

Consecutive interior angles, or angles on the same side of the transversal and between the two parallel lines, add up to 180 degrees.

What does it mean for angles to be 'in the same side' or 'on the same side' of a transversal?

Angles that are on the same side of a transversal refer to pairs of angles located on either the left or right of the transversal, but not split by it. These angles can be either consecutive interior or exterior angles.

How are alternate interior angles related?

Alternate interior angles are the pairs of angles that lie on opposite sides of the transversal and between the parallel lines. These angles are congruent, meaning they have equal measures.

What is the definition of 'consecutive exterior angles'?

Consecutive exterior angles are pairs of angles that lie on the same side of the transversal but outside the parallel lines. These angles also add up to 180 degrees.

How do you calculate an unknown angle using relationships between parallel lines?

To calculate an unknown angle, you can use the relationships between angles such as corresponding, vertically opposite, or consecutive interior angles. By knowing one angle, you can apply these rules to find the missing angle.

What is the relationship between alternate exterior angles?

Alternate exterior angles are the pairs of angles that lie on opposite sides of the transversal and outside the parallel lines. These angles are congruent to each other.

How can we use the angle relationships to solve problems involving parallel lines?

We can use angle relationships such as corresponding angles being equal, alternate interior angles being congruent, and consecutive interior angles adding up to 180 degrees to solve for unknown angles in problems involving parallel lines and a transversal.