Suma y diferencia de ángulos: problemas de trigonometría
Summary
TLDREn este video tutorial, el profesor explica cómo calcular la suma y diferencia de ángulos en trigonometría. Se presentan seis fórmulas clave para sumar o restar seno, coseno y tangente de ángulos, y cómo dependen del signo. Se utiliza el ejemplo práctico de calcular el seno, coseno y tangente de 15 grados a partir de los ángulos de 45 y 30 grados. El profesor guía paso a paso a través de las ecuaciones, destacando la importancia de aplicar las fórmulas correctamente y el cuidado con los signos. Además, ofrece recursos adicionales para práctica adicional.
Takeaways
- 📚 Se discuten las fórmulas para la suma y diferencia de ángulos en trigonometría.
- 🔢 Se presentan seis fórmulas para el seno, coseno y tangente de ángulos sumados o restados.
- ➡️ Se explica cómo cambiar el signo en las fórmulas dependiendo de la suma o resta de ángulos.
- 📐 Se utilizan las fórmulas para calcular el seno, coseno y tangente de 15 grados a partir de los ángulos 45 y 30 grados.
- 🧮 Se muestran los cálculos paso a paso para llegar a las soluciones numéricas.
- 📉 Se resalta la importancia de aplicar correctamente las fórmulas y prestar atención a los signos.
- 📝 Se sugiere que el conocimiento de estas fórmulas es fundamental para resolver problemas de trigonometría.
- 📊 Se menciona que los ángulos 45 y 30 grados son comunes en problemas de trigonometría y se utilizan para encontrar otros ángulos.
- 📖 Se ofrecen ejercicios con soluciones para practicar los conceptos aprendidos.
- 💬 Se invita a los espectadores a comentar dudas o aportar comentarios en la página web del video.
Q & A
¿Cuáles son las fórmulas para la suma y diferencia de seno, coseno y tangente de ángulos según el guion?
-Las fórmulas para la suma y diferencia de ángulos son: seno(a ± b) = seno(a)coseno(b) ± coseno(a)seno(b), coseno(a ± b) = coseno(a)coseno(b) ∓ seno(a)seno(b), y tangente(a ± b) = (tangente(a) ± tangente(b)) / (1 ∓ tangente(a)tangente(b)).
¿Cómo se determina el signo en las fórmulas de suma y diferencia de ángulos?
-El signo en las fórmulas de suma y diferencia de ángulos se determina según el tipo de operación (suma o resta) y el ángulo que se está calculando. Por ejemplo, en la fórmula de seno(a ± b), se utiliza '+' si es una suma y '-' si es una resta.
¿Qué significa el 'verde' mencionado en el guion al explicar las fórmulas de trigonometría?
-El 'verde' se refiere a los términos que se deben mantener iguales en las fórmulas de suma y diferencia de ángulos, como seno(a) y seno(b), o coseno(a) y coseno(b), para aplicar correctamente las fórmulas.
¿Cómo se calcula el seno de 15 grados utilizando las fórmulas de suma y diferencia de ángulos?
-Para calcular el seno de 15 grados, se utiliza la fórmula de resta de ángulos: seno(45 - 30) = seno(45)coseno(30) - coseno(45)seno(30), lo que da como resultado (√2/2)(√3/2) - (√2/2)(1/2), que simplifica a (√6 - √2)/4.
¿Cuál es el resultado numérico aproximado del seno de 15 grados según el guion?
-El resultado numérico aproximado del seno de 15 grados, según el guion, es (√6 - √2)/4, que se puede calcular con una calculadora para obtener un valor decimal.
¿Cómo se calcula el coseno de 15 grados utilizando las fórmulas del guion?
-El coseno de 15 grados se calcula con la fórmula de resta de ángulos: coseno(45 - 30) = coseno(45)coseno(30) + seno(45)seno(30), lo que resulta en (√2/2)(√3/2) + (√2/2)(1/2), que simplifica a (√6 + √2)/4.
¿Cuál es el resultado numérico aproximado del coseno de 15 grados según el guion?
-El resultado numérico aproximado del coseno de 15 grados, según el guion, es (√6 + √2)/4, que se puede obtener con una calculadora para obtener un valor decimal.
¿Cómo se calcula la tangente de 15 grados según el guion?
-La tangente de 15 grados se calcula con la fórmula de resta de ángulos: tangente(45 - 30) = (tangente(45) - tangente(30)) / (1 + tangente(45)tangente(30)), lo que resulta en (1 - √3/3) / (1 + 1*√3/3), que simplifica a 2 - √3.
¿Cuál es el resultado numérico aproximado de la tangente de 15 grados según el guion?
-El resultado numérico aproximado de la tangente de 15 grados, según el guion, es 2 - √3, que se puede calcular con una calculadora para obtener un valor decimal.
¿Cómo se pueden aplicar estas fórmulas para resolver problemas de trigonometría con ángulos diferentes?
-Estas fórmulas se pueden aplicar a problemas de trigonometría con ángulos diferentes cambiando los valores de a y b en las fórmulas para encontrar los seno, coseno y tangente de los ángulos resultantes.
¿Dónde pueden encontrarse ejercicios con soluciones para practicar más sobre la suma y diferencia de ángulos según el guion?
-Los ejercicios con soluciones para practicar más sobre la suma y diferencia de ángulos se pueden encontrar debajo del vídeo en la página web del profesor puntocom.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

✅ÁNGULOS COMPLEMENTARIOS Y SUPLEMENTARIOS| SUPER FÁCIL 💯| TRIGONOMETRÍA

Ángulo trigonométrico || Trigonometría 4to de Secundaria || Cap. 1

Identidades trigonométricas de suma de ángulos | Seno y Coseno de 75° sin calculadora

Matemática 1 TRIGONOMETRÍA 2da parte funciones trigonométricas en triángulos cualquiera

Ángulos I - Operaciones con las medidas de ángulos y bisectriz de un ángulo - Geometría
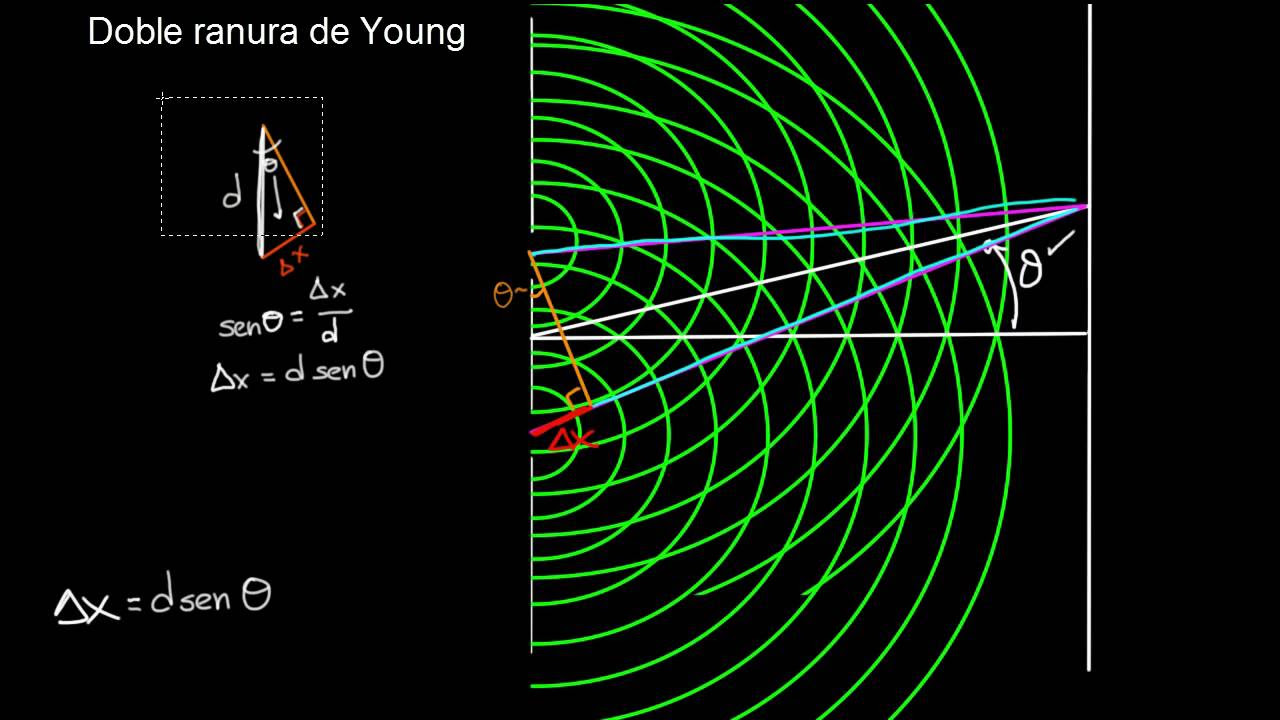
Doble ranura de Young. Parte 2 | Ondas de luz | Física | Khan Academy en Español
5.0 / 5 (0 votes)
