MAT 152 SAS 8 Video
Summary
TLDRThis Math 152 lesson focuses on computing measures of central tendency, crucial for understanding patterns in data sets. The instructor explains three key measures: mean, median, and mode. The mean, or average, is calculated by summing values and dividing by their count. The median is the middle value in an ordered set, unaffected by outliers. The mode is the most frequently occurring value. The lesson also covers weighted mean, which assigns different weights to values, and how to calculate these measures from grouped data using frequency distribution tables (FDT). Practical examples, such as calculating class averages, are provided to illustrate the concepts.
Takeaways
- 📊 Measures of central tendency are statistical methods used to find the middle or center of a data set, which helps in understanding patterns in various data types.
- 🔢 Mean, median, and mode are the three main measures of central tendency. Mean is calculated by summing all numbers and dividing by the count, median is the middle value when data is ordered, and mode is the most frequently occurring number.
- ⚖️ Weighted mean is a variation of the mean that assigns different weights to each number, reflecting their relative importance, unlike the simple mean which treats all numbers equally.
- 📈 The median is particularly useful as it is not affected by outliers, making it a robust measure of central tendency for skewed data sets.
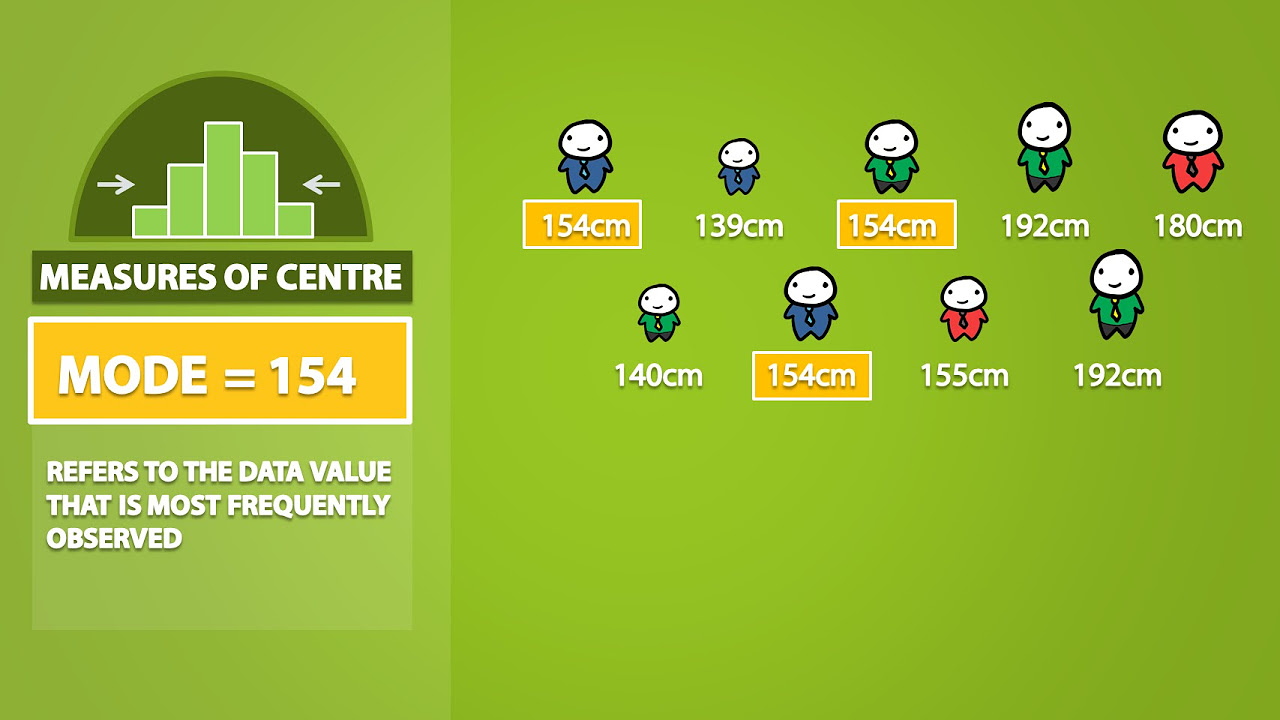
- 📚 The mode is the value that appears most frequently in a data set and can be used to identify the most common occurrence, but a data set can sometimes have no mode if no value repeats.
- 👨🏫 The lesson provides examples of calculating the mean, median, and mode from both ungrouped and grouped data, emphasizing the application of these measures in real-world scenarios like exam scores and financial data.
- 📋 When working with grouped data, the frequency distribution table (FDT) is used to calculate central tendencies by applying specific formulas that account for class intervals and frequencies.
- 🧮 The calculation of mean from grouped data involves summing the product of class marks and their frequencies (FX) and then dividing by the total number of observations (N).
- 📉 For the median in grouped data, the formula involves identifying the median class where the cumulative frequency is closest to half the total number of observations, and then calculating its value based on the class boundaries and frequencies.
- 🎯 The mode in grouped data is determined by identifying the class with the highest frequency, and then calculating its value using the lower class boundary, class size, and frequencies before and after the modal class.
- 📘 The lesson concludes with a practical example using an FDT of urine test results from 42 patients to calculate mean, median, and mode, demonstrating the application of these concepts in a health-related context.
Q & A
What is the main focus of the Math 152 lesson?
-The main focus of the Math 152 lesson is on computing measures of central tendency, specifically the mean, median, and mode, and understanding how to apply these measures to both ungrouped and grouped data.
What are the two learning targets mentioned in the lesson?
-The two learning targets are: 1) to compute measures of central tendency from ungrouped and grouped data, and 2) to identify the appropriate measures of central tendency for a given set of data.
What are measures of central tendency, and why are they important?
-Measures of central tendency are methods used to find the middle or center of a data set, giving a sense of where most data points are located. They are important in understanding patterns in populations, financial matters, and exam scores, among other applications.
How is the mean or average calculated?
-The mean is calculated by adding all the numbers in a data set together and then dividing the sum by the total number of values in the set.
What is the difference between a regular mean and a weighted mean?
-A regular mean treats all numbers equally, while a weighted mean assigns different weights to each number, making some values count more in the calculation.
How is the median determined in a data set?
-The median is the middle number when a data set is arranged in order. If the data set has an odd number of values, the median is the middle value. If it has an even number of values, the median is the average of the two middle numbers.
What is the mode, and how is it identified?
-The mode is the number that appears most often in a data set. It is identified by finding the value that occurs with the highest frequency.
How is the weighted mean calculated in the provided example?
-In the provided example, the weighted mean is calculated by multiplying each class's average grade by the number of students in that class, summing these products, and then dividing by the total number of students.
What are the steps for calculating the mean, median, and mode from grouped data using the Frequency Distribution Table (FDT)?
-The steps include identifying the frequencies, class marks, and cumulative frequencies, then applying the formulas for mean, median, and mode, considering factors like class boundaries and sizes.
What are the key takeaways regarding median and modal classes?
-The median and modal classes can be the same or different. There can be more than one modal class if multiple classes have the same highest frequency. If the modal class is the first or last class, the frequency before or after may be zero.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Tutorial 4- Measure Of Central Tendency- Mean, Median And Mode In Hindi

Range, variance and standard deviation as measures of dispersion | Khan Academy

Lecture 3.2 - Describing Numerical Data - Mean
Statistik Deskriptif
Mode, Median, Mean, Range, and Standard Deviation (1.3)

Mathematics in the Modern World - Data Management (Part 1)
5.0 / 5 (0 votes)