Teorema Pythagoras [Part 1] - Menentukan Panjang Salah Satu Sisi Pada Segitiga Siku-siku
Summary
TLDRIn this video, Pak Beni introduces the Pythagorean Theorem and its applications for right-angled triangles. He explains the concept of the hypotenuse as the side opposite the right angle and demonstrates how to calculate the length of any side using the formula a² + b² = c². Through clear examples, he shows how to find both the hypotenuse and the other sides, including more complex cases with overlapping triangles. The video emphasizes understanding the concept over memorizing letters and encourages practice through exercises. It serves as a practical guide for applying the theorem in real-world and mathematical problems.
Takeaways
- 😀 The video introduces the Pythagorean Theorem and aims to help students determine the length of one side in a right-angled triangle.
- 😀 Understanding the Pythagorean Theorem involves recognizing the three sides of a right-angled triangle: the hypotenuse (longest side) and the other two sides that meet at the right angle.
- 😀 The fundamental formula for the Pythagorean Theorem is: c² = a² + b², where c is the hypotenuse, and a and b are the other sides.
- 😀 The hypotenuse is always opposite the right angle, and it is the longest side of a right-angled triangle.
- 😀 The variables used in the theorem (a, b, c) can vary in naming, but the key concept is to identify the longest side (hypotenuse) and apply the formula correctly.
- 😀 To solve problems using the Pythagorean Theorem, you do not need to memorize specific letters. Focus on understanding the relationship between the sides.
- 😀 To find the hypotenuse, square the lengths of the other two sides and then take the square root of the sum.
- 😀 To find a missing side, subtract the square of one side from the square of the hypotenuse and take the square root of the result.
- 😀 Practical examples are provided in the video, such as finding the length of the hypotenuse (e.g., 12 and 16 give a hypotenuse of 20) and solving for a missing side using subtraction (e.g., hypotenuse of 13, side of 5, missing side is 12).
- 😀 The video encourages students to practice with similar problems and check their answers in the video description.
Q & A
What is the main topic of Pak Beni's video?
-The main topic of Pak Beni's video is the Pythagorean Theorem, specifically focusing on how to determine the length of one side in a right triangle.
What is the Pythagorean Theorem formula mentioned in the video?
-The Pythagorean Theorem formula presented in the video is: c² = a² + b², where 'c' represents the hypotenuse (the longest side of a right triangle), and 'a' and 'b' represent the other two sides.
What is the significance of the hypotenuse in a right triangle?
-The hypotenuse is the longest side of a right triangle, opposite the right angle. It is crucial in the Pythagorean Theorem, as it relates to the other two sides of the triangle.
What practical fields can benefit from the Pythagorean Theorem, as mentioned in the video?
-The Pythagorean Theorem is useful in fields such as architecture, navigation, surveying, and topography.
How does Pak Beni suggest we approach understanding the Pythagorean Theorem?
-Pak Beni emphasizes understanding the concept of the hypotenuse and its relationship to the other sides of a right triangle, rather than memorizing the specific letters used in the formula.
How do you determine the hypotenuse in a right triangle from the video examples?
-To determine the hypotenuse, look for the side opposite the right angle. In the examples, it is clearly marked as the longest side of the triangle.
In the first example, what is the value of x in the equation x² = 12² + 16²?
-In the first example, solving x² = 12² + 16² gives x² = 144 + 256, resulting in x² = 400. Taking the square root of 400, x = 20.
How is the second example different from the first one in terms of the Pythagorean Theorem?
-The second example involves finding a missing side of the triangle (x) using subtraction. The equation becomes x² = 13² - 5², leading to x² = 169 - 25, which simplifies to x² = 144. Thus, x = 12.
What is the method used to find the length of side AB in the complex triangle example?
-In the complex triangle example, the length of side AB is found using the Pythagorean Theorem. First, calculate AB in triangle ABC using the formula AB² = 40² - 24², which gives AB = 32 cm.
What role does dividing the large triangle into two smaller triangles play in solving the problem?
-Dividing the large triangle into two smaller right triangles (ABC and BCD) allows for easier calculation of the missing sides using the Pythagorean Theorem separately in each triangle, making the overall problem solvable.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Kurikulum Merdeka Matematika Kelas 8 Bab 2 Teorema Pythagoras
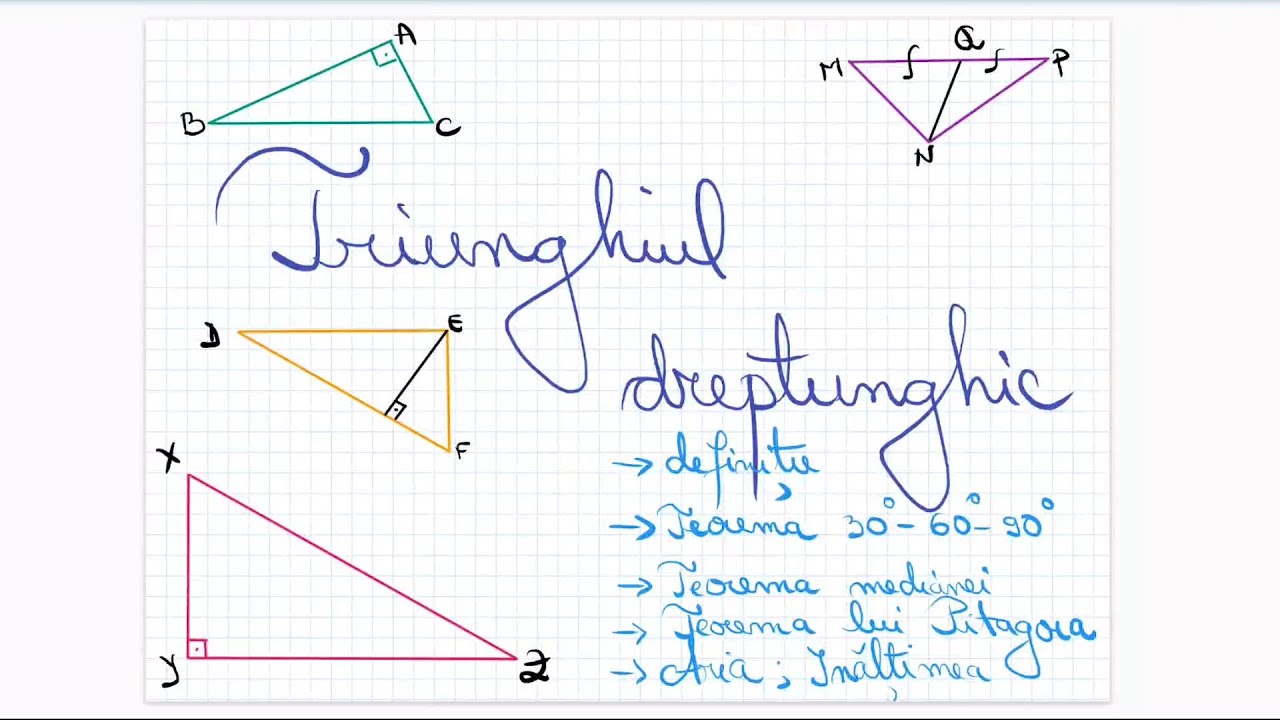
Triunghiul dreptunghic, teorema 30 60 90, teorema medianei, teorema lui Pitagora si reciproca, arie

Class 10 Maths | Chapter 6 | Introduction | Triangles | NCERT
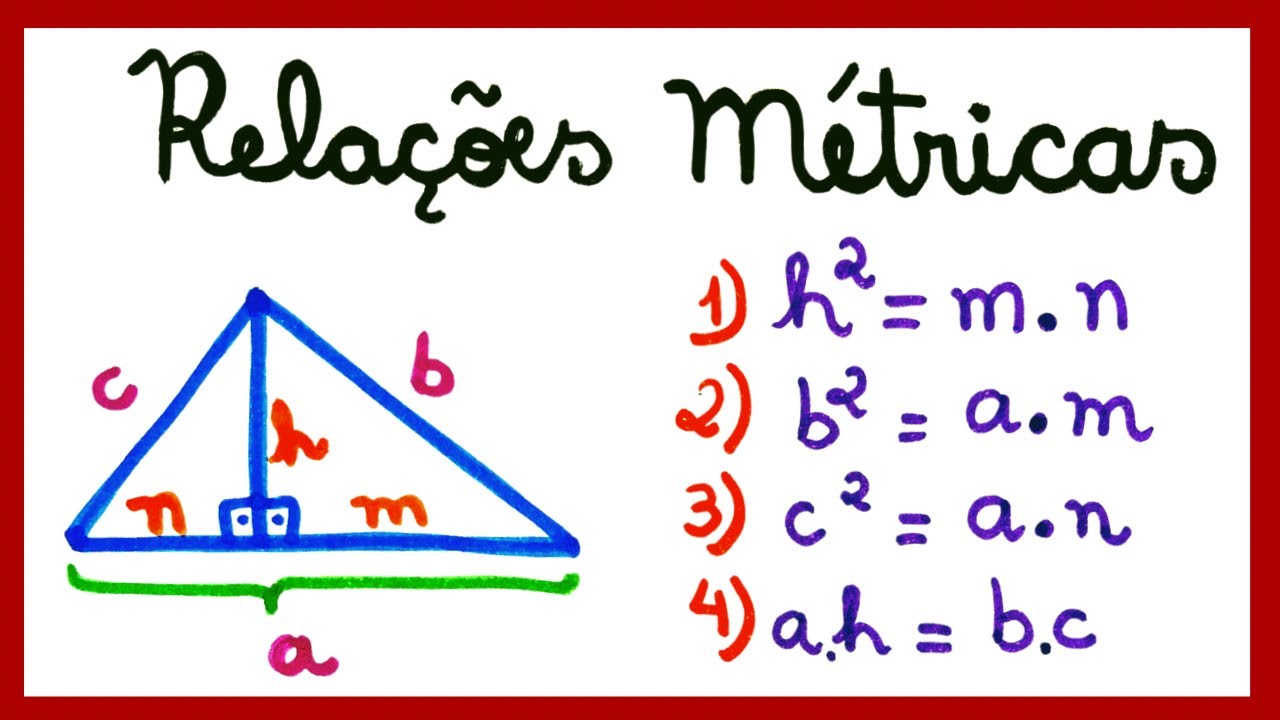
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO!!

Teorema Pythagoras (Teopyras)- alat peraga matematika, media Pembelajaran Matematika
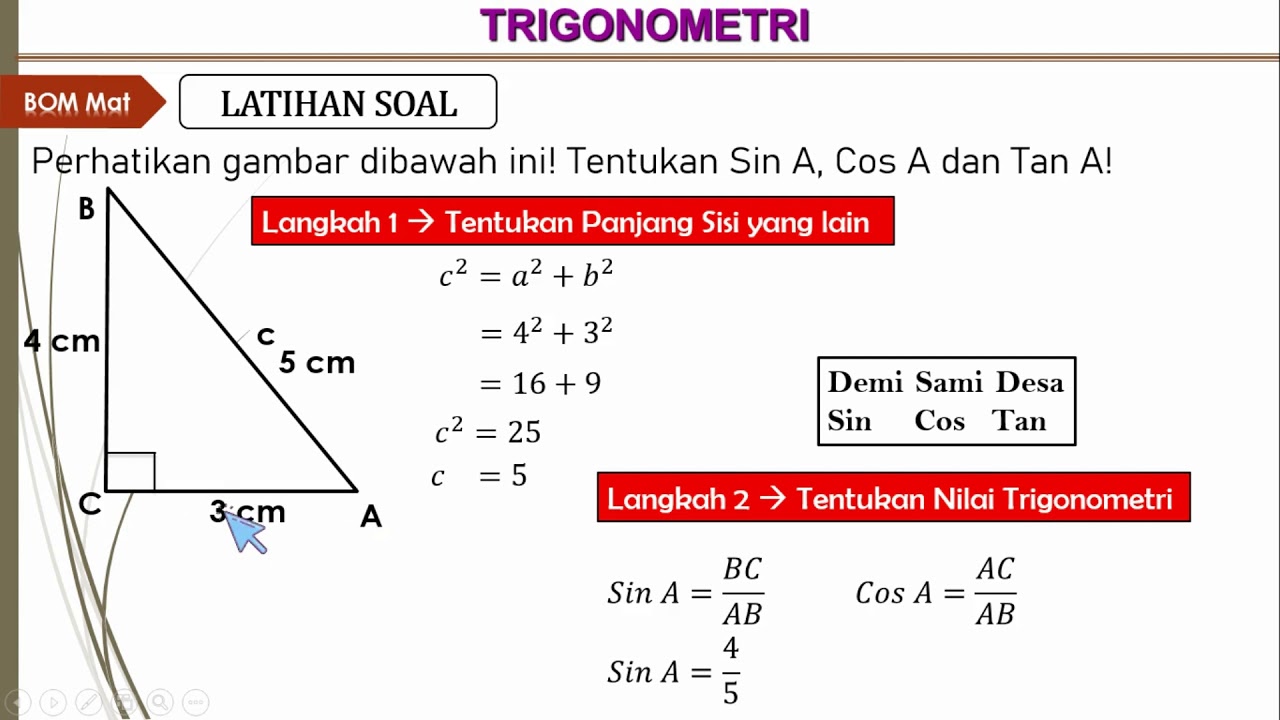
Perbandingan trigonometri pada segitiga siku siku, Menjelaskan rasio trigonometri
5.0 / 5 (0 votes)
