Cálculo de Áreas por Aproximación
Summary
TLDREste video ofrece una introducción al cálculo de áreas por aproximación en el contexto del cálculo integral. Se explora el uso de rectángulos para estimar áreas de figuras no convencionales, destacando la importancia de la teoría y la explicación detallada para facilitar el entendimiento independientemente de la presencia del profesor. Seguidamente, se presentan ejemplos prácticos y se desafía a los estudiantes a idear soluciones creativas, promoviendo el pensamiento crítico y la aplicación de conceptos de cálculo diferencial y integral.
Takeaways
- 📘 El objetivo del video es facilitar el regreso a clases y la realización de actividades con cuadernillos bien estructurados y teoría clara.
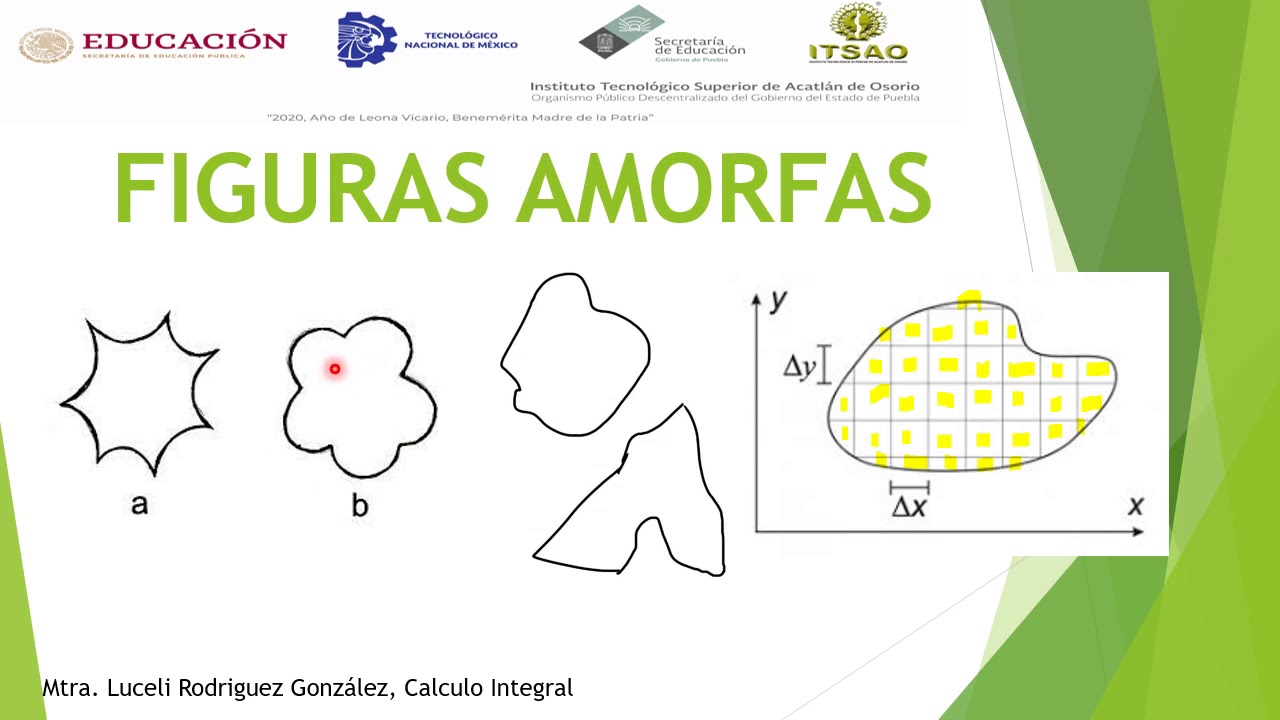
- 📐 Se aborda el cálculo de áreas por aproximación, destacando la importancia de la relación entre el cálculo de áreas y el cálculo integral y diferencial.
- 🤔 Se invita a los estudiantes a pensar creativa y no limitarse al uso de rectángulos y cuadrados para calcular áreas de figuras no convencionales.
- 📈 Se enseña cómo estimar el área de figuras geométricas no bien definidas a través de la construcción de figuras geométricas conocidas dentro de la nueva figura.
- 📉 Se explica el proceso de dibujo de rectángulos a lo largo del eje x y cómo calcular sus alturas utilizando la función dada.
- 🔍 Se resalta la importancia de entender que los cálculos son aproximaciones y no áreas exactas.
- 📊 Se discute cómo aumentar el número de rectángulos puede mejorar la precisión de la aproximación al área.
- 📏 Se calcula el ancho de los rectángulos a partir del intervalo total dividido por el número de rectángulos.
- 🔢 Se generaliza el proceso para cualquier función dada, utilizando variables para representar los puntos y los rectángulos.
- 📖 Se enfatiza la importancia de practicar y aplicar estos conceptos en ejercicios adicionales para un entendimiento más profundo.
Q & A
¿Por qué se eligió el cuadernillo utilizado en la clase?
-El cuadernillo fue escogido porque tiene una estructura más clara y explicativa que otros disponibles, facilitando la comprensión de los temas sin necesidad de videos o constante apoyo del profesor.
¿Cuál es el objetivo del regreso a clases según el profesor?
-El objetivo es que los estudiantes encuentren sencillo realizar las actividades y que los cuadernillos proporcionen teoría de forma clara y bien explicada para que puedan resolver los ejercicios por sí mismos.
¿Qué método utiliza el profesor para enseñar el cálculo de áreas no convencionales?
-El profesor enseña el cálculo de áreas no convencionales utilizando aproximaciones con figuras geométricas conocidas, como rectángulos, que se dibujan dentro de la figura irregular.
¿Qué sucede al usar rectángulos por debajo y por encima de una curva?
-Al usar rectángulos por debajo de una curva, el área estimada es menor que el área real, mientras que al usar rectángulos por encima de la curva, el área es mayor.
¿Cómo afecta el número de rectángulos al cálculo de áreas?
-A medida que se incrementa el número de rectángulos, el ancho de cada uno disminuye y la suma de sus áreas se aproxima más al área real de la figura.
¿Qué cambios se producen al aumentar el número de rectángulos en la suma de áreas?
-Al aumentar el número de rectángulos, la suma de las áreas se vuelve más precisa, acercándose más al valor real del área de la figura.
¿Cómo se calcula el ancho de cada rectángulo en una aproximación?
-El ancho de cada rectángulo se calcula dividiendo el intervalo total en el eje x (desde el inicio hasta el final de la figura) entre el número de rectángulos deseados.
¿Cuál es la fórmula general para el cálculo de áreas utilizando rectángulos?
-La fórmula general consiste en multiplicar el ancho de cada rectángulo (delta x) por la altura correspondiente, que se calcula con la función evaluada en los puntos del extremo izquierdo de cada rectángulo.
¿Cómo se relacionan los conceptos de cálculo diferencial e integral con el cálculo de áreas?
-El cálculo de áreas por aproximación está vinculado tanto al cálculo integral, que se enfoca en sumar áreas pequeñas, como al cálculo diferencial, que ayuda a determinar las funciones y límites involucrados.
¿Qué recomienda el profesor hacer tras entender el tema de cálculo de áreas por aproximación?
-El profesor recomienda que los estudiantes apliquen el procedimiento aprendido en los ejercicios del cuadernillo, tanto en las actividades de cierre como en las secciones de práctica adicional.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
Figuras amorfas y notación sumatoria

Calculo integral

¿Qué es la Integral Definida? | Videos Educativos Aula365

Cálculo de variación: Construcción histórica.

INTEGRALI - introduzione al calcolo integrale _ NT03

Curso de Integrales. Capítulo 1: ¿Qué es y para qué sirve la integral? Una propuesta didáctica.
5.0 / 5 (0 votes)
