Electrical Engineering: Basic Laws (9 of 31) Kirchhoff's Laws: A Simple Example

Summary

This lecture provides an introduction to using Kirchhoff's laws in simple electrical circuits, particularly focusing on a series loop circuit. The instructor explains the concept of series circuits, node sharing, and reference voltage using ground. They calculate current using Ohm's law, showing how Kirchhoff’s Voltage Law (KVL) applies by summing voltages around the loop, which should equal zero. The example highlights the simplicity of using Ohm’s law in such circuits but emphasizes that Kirchhoff’s laws are crucial for solving more complex circuits with multiple branches and voltage sources.

Takeaways

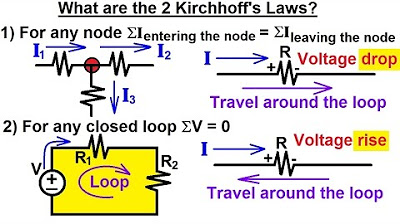
• 🔄 The circuit discussed is a simple series loop where all components are connected in series, meaning each component shares only a single node with another component.
• ⚡ The circuit is connected to ground, which serves as a reference point set to zero volts, ensuring consistent voltage measurements.
• 🔋 The lecture explains the process of summing voltages around a loop using Kirchhoff's Voltage Law (KVL), stating that the sum of all voltages should equal zero.
• 📐 Kirchhoff’s Current Law (KCL) is mentioned, but since there’s only one loop, it’s not essential for this simple circuit as the current is the same throughout.
• 📏 Ohm's Law (V = IR) is used to calculate the current in the circuit, given that the total voltage is 40 volts and the total resistance is 10 ohms (R1 + R2).
• 💡 The calculated current in the circuit is 4 amps, based on the total resistance and voltage.
• ➖ When calculating the voltage drops across each resistor, the first resistor (2 ohms) results in an 8-volt drop, and the second resistor (8 ohms) causes a 32-volt drop.
• ✅ Verifying Kirchhoff's Voltage Law, the voltage rise across the battery is 40 volts, and the sum of the voltage drops across the resistors (8V + 32V) equals this rise, satisfying KVL.
• 🔧 While KVL is useful in this basic example, the video notes that Kirchhoff's Laws become essential in more complex circuits with multiple branches and voltage sources.
• 🧠 The lecture demonstrates that Kirchhoff’s Laws, combined with Ohm's Law, can simplify the analysis of circuits, especially in more complex situations.

Q & A

What type of circuit is being discussed in the script?

The script discusses a series circuit, where all components are connected in series, meaning any two components share a single node between them that is not shared by any other component.

What is the significance of connecting the circuit to ground?

Connecting the circuit to ground means that a part of the circuit is at zero volts, serving as a reference voltage. This is done by connecting the circuit to a conductive material that can absorb or release charges to maintain this zero-volt condition.

How is Kirchhoff's Voltage Law applied in this circuit?

Kirchhoff's Voltage Law (KVL) states that the sum of all voltages around a closed loop must equal zero. In the script, the sum of the voltage rise across the battery and the voltage drops across the resistors is shown to equal zero, confirming KVL.

How do you calculate the current in a series circuit using Ohm’s Law?

In a series circuit, the current can be calculated using Ohm’s Law (I = V/R). Here, the total resistance is the sum of all resistances in the circuit, and the current is equal to the total voltage divided by the total resistance.

What are the voltage drops across the resistors in the example circuit?

In the example circuit, the voltage drop across the first resistor (R1 = 2 ohms) is 8 volts, and the voltage drop across the second resistor (R2 = 8 ohms) is 32 volts.

Why is Kirchhoff’s Current Law not very useful in this example?

Kirchhoff’s Current Law (KCL) is not very useful in this example because there is only one current flowing through the entire series circuit, meaning the current entering and leaving each node is the same, so KCL doesn't provide additional insights.

What is the total resistance in the example circuit?

The total resistance in the example circuit is the sum of the two resistors, R1 and R2. Therefore, the total resistance is 2 ohms + 8 ohms = 10 ohms.

How much current flows through the circuit in the example?

The current flowing through the circuit is calculated as I = V / (R1 + R2) = 40 volts / 10 ohms = 4 amps.

Why is Kirchhoff’s Voltage Law important in circuit analysis?

Kirchhoff’s Voltage Law is important because it allows you to verify that the sum of all voltage rises and drops around any closed loop in a circuit equals zero, ensuring energy conservation and helping in analyzing complex circuits.

When would Kirchhoff’s Laws be more useful in circuit analysis?

Kirchhoff’s Laws become much more useful when analyzing complex circuits with multiple branches, voltage sources, and current paths. They help in calculating the currents and voltages across different parts of the circuit in such cases.