GRAFICAR FUNCIONES LINEALES Super facil
Summary
TLDRDaniel Carrión presenta un tutorial sobre cómo graficar funciones lineales, repasando conceptos básicos del plano cartesiano y utilizando ecuaciones de primer grado. El video guía a los espectadores a crear una tabla de valores para x y y, a partir de ella, a trazar puntos en el plano y conectarlos para formar la línea recta representativa de la función. Además, muestra cómo se puede graficar una función lineal con tan solo dos puntos, ilustrando con ejemplos prácticos y animando a la práctica y participación en redes sociales.
Takeaways
- 📚 Daniel Carrión enseña cómo graficar funciones lineales en un plano cartesiano.
- 📐 El plano cartesiano consiste en dos rectas numéricas, una horizontal (eje de las abscisas) y otra vertical (eje de las ordenadas), que se cortan en el origen.
- 🔢 Las ecuaciones de primer grado, también conocidas como ecuaciones lineales, implican exponentes con valor 1.
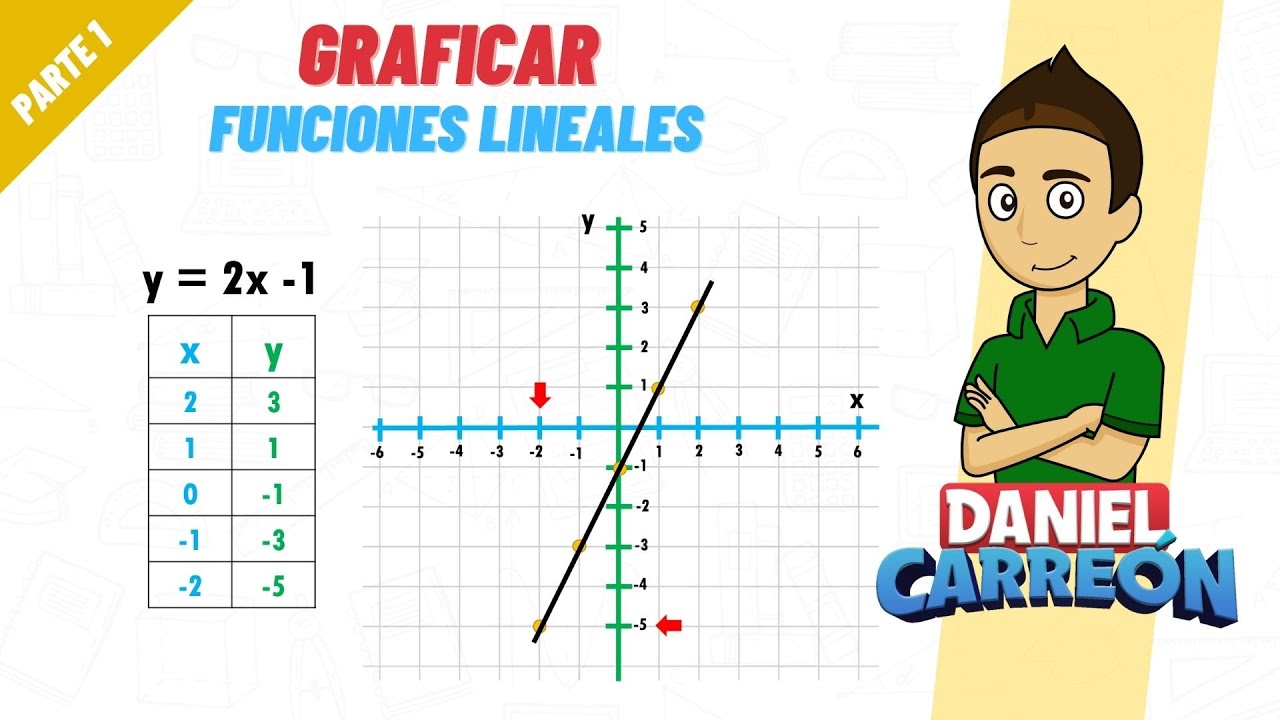
- 📈 Para graficar una función lineal, se proponen valores para la variable x y se calcula el correspondiente valor de y.
- 📝 Se crea una tabla con los valores de x e y, obtenidos al sustituir los valores de x en la función dada.
- 📍 Se grafican los puntos obtenidos en el plano cartesiano y se conectan para formar una línea recta.
- 👉 Se puede graficar una función lineal usando tan solo dos puntos, siempre y cuando se elijan adecuadamente.
- 📐 En el ejemplo dado, la función y = 2x - 1 se grafica utilizando puntos como (2, 3), (1, 1), (0, -1) y (-1, -3).
- 📉 Otro ejemplo muestra cómo graficar la función y = 4x - 2 utilizando solo dos puntos, como (1, 2) y (-1, -6).
- 📚 Las funciones lineales son importantes en matemáticas y tienen aplicaciones en diversos campos.
- 💻 Se anima a los espectadores a practicar y enviar sus propios ejercicios de funciones lineales a las redes sociales del canal.
Q & A
¿Quién es el presentador del video sobre graficar funciones lineales?
-El presentador del video es Daniel Carrión.
¿Qué es el plano cartesiano y qué componentes tiene?
-El plano cartesiano está formado por dos rectas numéricas, una horizontal llamada eje de las abscisas o de las equis, y otra vertical llamada eje de las ordenadas, que se cortan en un punto conocido como el origen.
¿Qué tipo de ecuaciones se discuten en el video?
-El video trata sobre ecuaciones de primer grado, también conocidas como ecuaciones lineales, debido a que su gráfica es una línea recta.
¿Cómo se proponen los valores para x en el ejemplo dado en el video?
-Se proponen valores para x como 2, 10, -1 y -2, aunque se puede elegir cualquier valor, se recomienda incluir 0 y valores tanto positivos como negativos.
¿Cómo se encuentra el valor de y a partir de la función y y los valores de x?
-Se sustituye el valor de x en la función dada y se realiza el cálculo para encontrar el correspondiente valor de y.
¿Cuál es la función lineal que se utiliza para el primer ejemplo en el video?
-La función lineal utilizada es y = 2x - 1.
¿Cómo se grafican las funciones lineales en el plano cartesiano?
-Se grafican las funciones lineales encontrando los puntos de intersección en el plano cartesiano a partir de los valores de x e y calculados y luego se conectan con una línea recta.
¿Por qué se dice que las funciones lineales son 'lineales'?
-Se llaman funciones lineales porque las variables en la ecuación están elevadas a la primera potencia, lo que resulta en una gráfica de una línea recta.
¿Cuántos puntos son necesarios para graficar una función lineal según el ejemplo del video?
-Según el ejemplo del video, aunque se pueden graficar más, se puede graficar una función lineal con tan solo dos puntos.
¿Cómo se demuestra en el video que una función lineal puede ser graficada con solo dos puntos?
-Se da un segundo ejemplo en el video donde se grafica la función y = 4x - 2 utilizando solo dos puntos calculados a partir de los valores x = 1 y x = -1.
¿Cómo se pueden enviar las prácticas de las funciones lineales al presentador del video?
-Se pueden enviar las prácticas de las funciones lineales al presentador a través de sus redes sociales.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
GRAFICAR FUNCIONES LINEALES PARTE 1

GRAFICAR FUNCIONES CUADRÁTICAS Super facil
RESOLVER SISTEMAS DE ECUACIONES MÉTODO DE GRAFICACIÓN Super fácil - Para principiantes

INECUACIONES DE PRIMER GRADO pte1 Super facil - Para principiantes

SISTEMA DE ECUACIONES POR MÉTODO DE CRAMER O DETERMINANTES Super fácil - Para principiantes

ECUACIONES DE SEGUNDO GRADO POR FACTORIZACIÓN Super facil - Para principiantes
5.0 / 5 (0 votes)
