SPLDV - Metode Eliminasi
Summary
TLDRIn this tutorial, Neneng Kurniawati explains how to solve a system of linear equations with two variables using the elimination method. She first introduces the method, emphasizing how to eliminate one variable to find the value of the other. Using examples, she demonstrates step-by-step how to eliminate variables and solve for unknowns in equations like x - y = 1 and 2x - y = 4. The video also compares the elimination method to other methods such as substitution and graphical solutions, helping viewers choose the most suitable approach for solving linear equations.
Takeaways
- 😀 The video introduces the elimination method for solving systems of linear equations with two variables.
- 😀 The goal of the elimination method is to eliminate one variable by manipulating the system of equations, making it easier to solve for the other variable.
- 😀 To use the elimination method, equations should be arranged in the same order before proceeding with elimination.
- 😀 One of the key steps in the elimination method is to equate the coefficients of one of the variables in both equations.
- 😀 Once the coefficients of the variable are the same, the variables can be eliminated by adding or subtracting the equations.
- 😀 After eliminating one variable, the remaining equation can be solved for the other variable.
- 😀 For example, when solving x - y = 1 and 2x - y = 4, subtracting the two equations results in eliminating y, allowing for solving x.
- 😀 Once x is found, the value can be substituted into one of the original equations to solve for y.
- 😀 The video also covers solving a system with a more complex equation set, such as 2x + 4y = 8 and 3x - y = -9, demonstrating the use of least common multiples (LCM) to eliminate a variable.
- 😀 The method requires multiplying equations to align the coefficients of a variable, allowing for elimination by adding or subtracting.
- 😀 After eliminating the first variable and solving for the second, the process concludes with the solution for both variables in the system.
Q & A
What is the elimination method for solving systems of linear equations?
-The elimination method involves eliminating one variable by adding or subtracting equations to make it disappear, leaving a simpler equation to solve for the remaining variable.
What are the first steps to use the elimination method?
-The first step is to put the two equations in the same order. Then, equate the coefficient of one variable so that it can be eliminated by adding or subtracting the equations.
Why do we need to equate the coefficients of one variable in the elimination method?
-Equating the coefficients of one variable ensures that when the equations are added or subtracted, that variable will cancel out, allowing you to solve for the other variable.
How do we eliminate a variable when solving a system using the elimination method?
-To eliminate a variable, you either add or subtract the equations after ensuring that the coefficients of the variable are the same in both equations.
In the example where x - y = 1 and 2x - y = 4, what is the first step to solve for x using the elimination method?
-The first step is to eliminate y. Since the coefficient of y is -1 in both equations, you subtract the first equation from the second equation to eliminate y.
How do you solve for y in the system of equations 2x + 4y = 8 and 3x - y = -9?
-To solve for y, you first eliminate x by equating the coefficients of x. You do this by multiplying the equations so that the x coefficients are the same, and then subtracting the equations to eliminate x.
What is the significance of the least common multiple (LCM) in the elimination method?
-The LCM helps to find a common multiple of the coefficients of the variable you want to eliminate, making it possible to multiply the equations accordingly and eliminate one of the variables.
In the case of 2x + 4y = 8 and 3x - y = -9, how do you find the LCM of the coefficients of x?
-The LCM of 2 and 3 (the coefficients of x in both equations) is 6. Multiply the first equation by 3 and the second equation by 2 so that the x coefficients are both 6.
What happens after eliminating one variable in the elimination method?
-After eliminating one variable, you are left with a single equation with one variable. This allows you to solve for that variable. Once you have its value, you can substitute it back into one of the original equations to find the value of the other variable.
Can the elimination method give different results from the substitution and graphical methods?
-No, all methods—elimination, substitution, and graphical—will yield the same results for a system of linear equations. The difference lies in the approach and ease of use depending on the problem.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Kurikulum Merdeka Matematika Kelas 9 Bab 1 Sistem Persamaan Linear Dua Variabel
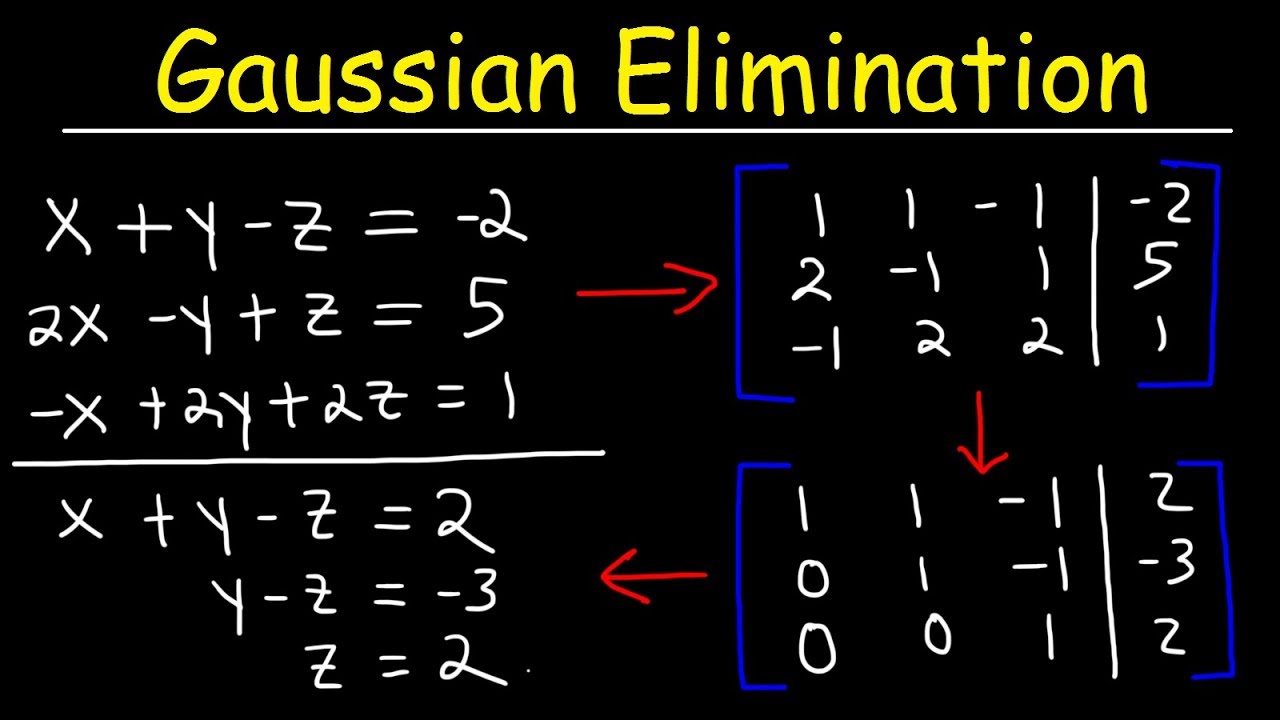
Gaussian Elimination & Row Echelon Form

Cara menentukan himpunan penyelesaian sistem persamaan linear tiga variabel

SPLTV #Part 4 // Metode Gabungan // Sistem Persamaan Linear Tiga Variabel

Matematika kelas X - Sistem Persamaan Linear part 1 - Sistem Persamaan Linear Dua Variabel (SPLDV)
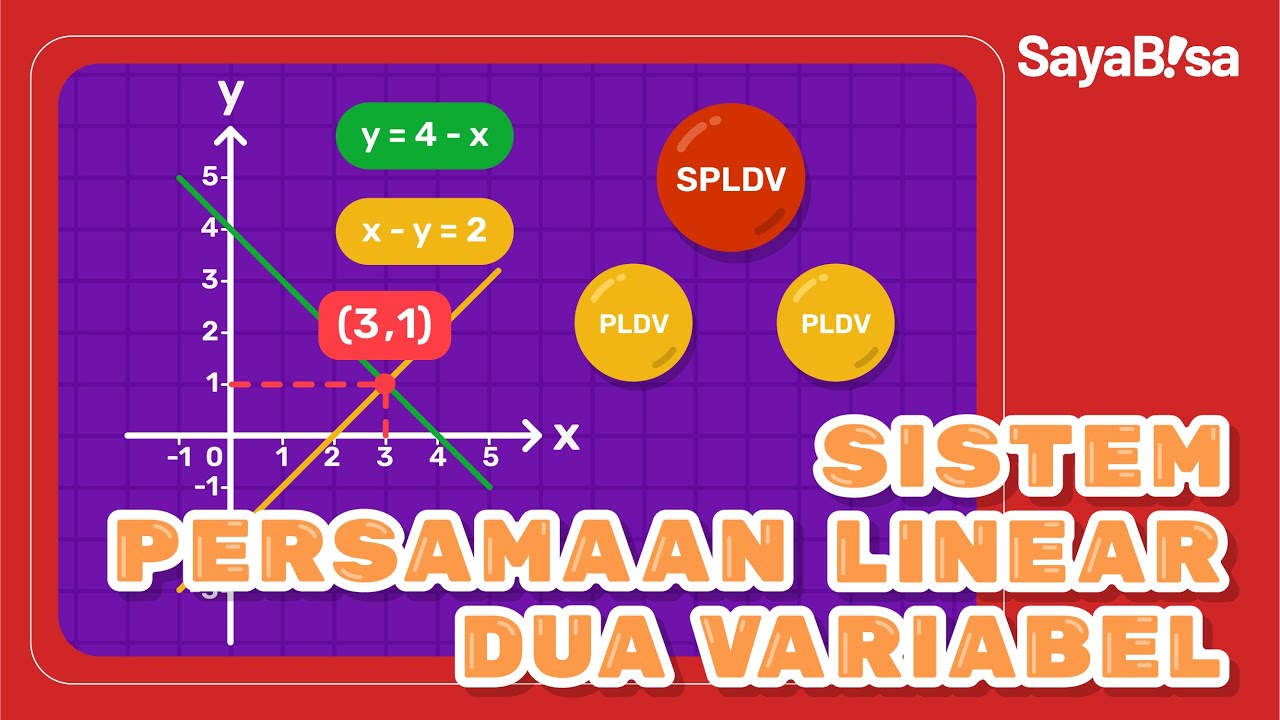
Sistem Persamaan Linear Dua Variabel | Matematika | SayaBisa
5.0 / 5 (0 votes)
