Kurikulum Merdeka Matematika Kelas 9 Bab 1 Sistem Persamaan Linear Dua Variabel

Summary

This educational video explains how to solve systems of linear equations with two variables (SPLDV) using four methods: graphing, substitution, elimination, and a combined approach. The video walks through each method with clear examples, demonstrating how to find solutions for different equations step by step. Graphing involves plotting the equations and identifying the intersection point, while substitution and elimination focus on manipulating the equations to solve for variables. The combined method integrates elimination and substitution for efficient problem-solving. The video aims to help students understand and apply these methods to solve linear equations effectively.

Takeaways

• 😀 SPLDV stands for 'Sistem Persamaan Linear Dua Variabel', which is the system of linear equations with two variables.
• 😀 In 7th grade, students learn about linear equations with one variable, and now in 9th grade, they progress to equations with two variables.
• 😀 There are four primary methods to solve systems of linear equations: Graphing, Substitution, Elimination, and Combination.
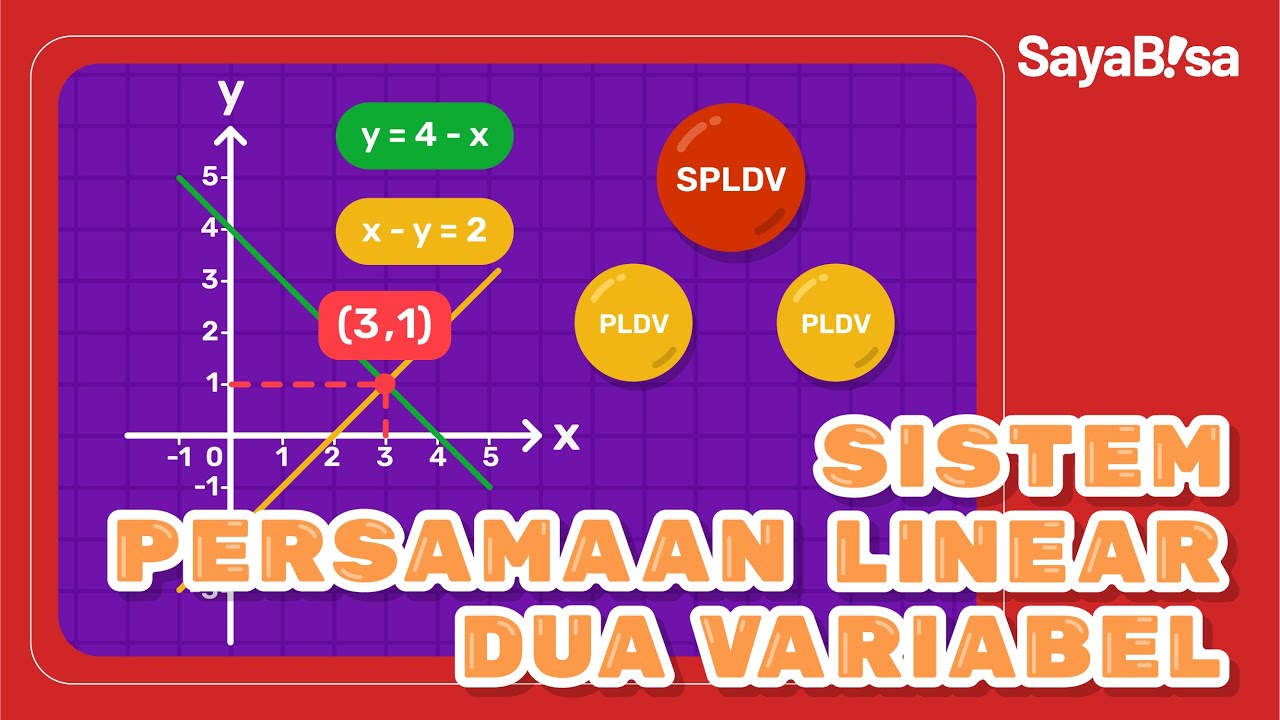
• 😀 The **Graphing Method** involves plotting the equations on a Cartesian plane and finding the point where the lines intersect, which gives the solution.
• 😀 The **Substitution Method** involves solving one equation for one variable and substituting that value into the other equation to find the second variable.
• 😀 In the **Elimination Method**, you eliminate one variable by manipulating the equations and solving for the other variable.
• 😀 The **Combination Method** is a blend of the Elimination and Substitution methods, starting with elimination and then using substitution for the final solution.
• 😀 To solve using the Graphing Method, first, set one variable (either x or y) to 0 in each equation, then plot the points on a graph.
• 😀 In the Substitution Method, after solving for one variable, substitute it into the other equation and solve for the second variable.
• 😀 The Elimination Method involves multiplying the equations if necessary to align variables, then subtracting or adding them to eliminate one variable and solve for the other.
• 😀 By practicing different methods, students can improve their ability to solve complex systems of linear equations efficiently.

Q & A

What is SPLDV and what does it stand for?

SPLDV stands for 'Sistem Persamaan Linear Dua Variabel', which is the system of linear equations with two variables. It involves solving equations where there are two unknowns (typically x and y).

How does the graphical method work in solving a system of linear equations?

In the graphical method, you plot the equations on a Cartesian plane. The solution to the system is the point where the lines representing the equations intersect.

What steps are involved when using the graphical method?

First, create a table of values for both equations by setting x or y to zero and solving for the other variable. Then, plot these points on a graph and find where the lines intersect, which gives the solution.

What is the substitution method?

The substitution method involves solving one equation for one variable and then substituting that expression into the other equation to find the value of the second variable.

Can you explain the steps involved in the substitution method with an example?

First, choose one equation and solve for one variable, say x. Then, substitute this expression for x into the other equation. After solving for y, substitute the value of y back into the first equation to find x.

What is the main idea behind the elimination method?

The elimination method involves adding or subtracting the two equations to eliminate one variable, making it easier to solve for the other variable.

How do you apply the elimination method step by step?

First, align the two equations and then multiply them by suitable factors to make the coefficients of one variable equal. Next, either add or subtract the equations to eliminate one variable and solve for the other.

What does the combined method involve?

The combined method is a mix of both elimination and substitution methods. First, eliminate one variable using the elimination method, and then substitute the result into one of the original equations to solve for the second variable.

What is the solution to the system of equations 2x + y = 5 and x - 2y = 0 using the elimination method?

First, multiply the second equation by 2 to match the coefficients of y, then subtract the equations to eliminate y. This gives y = 1. Substituting y = 1 into the first equation gives x = 2. So, the solution is (2, 1).

Why is it important to choose the correct method for solving a system of linear equations?

Choosing the right method depends on the specific system of equations. The graphical method works best for visualizing the solution, while substitution and elimination methods are more efficient for exact calculations. The combined method is useful when both elimination and substitution are required.