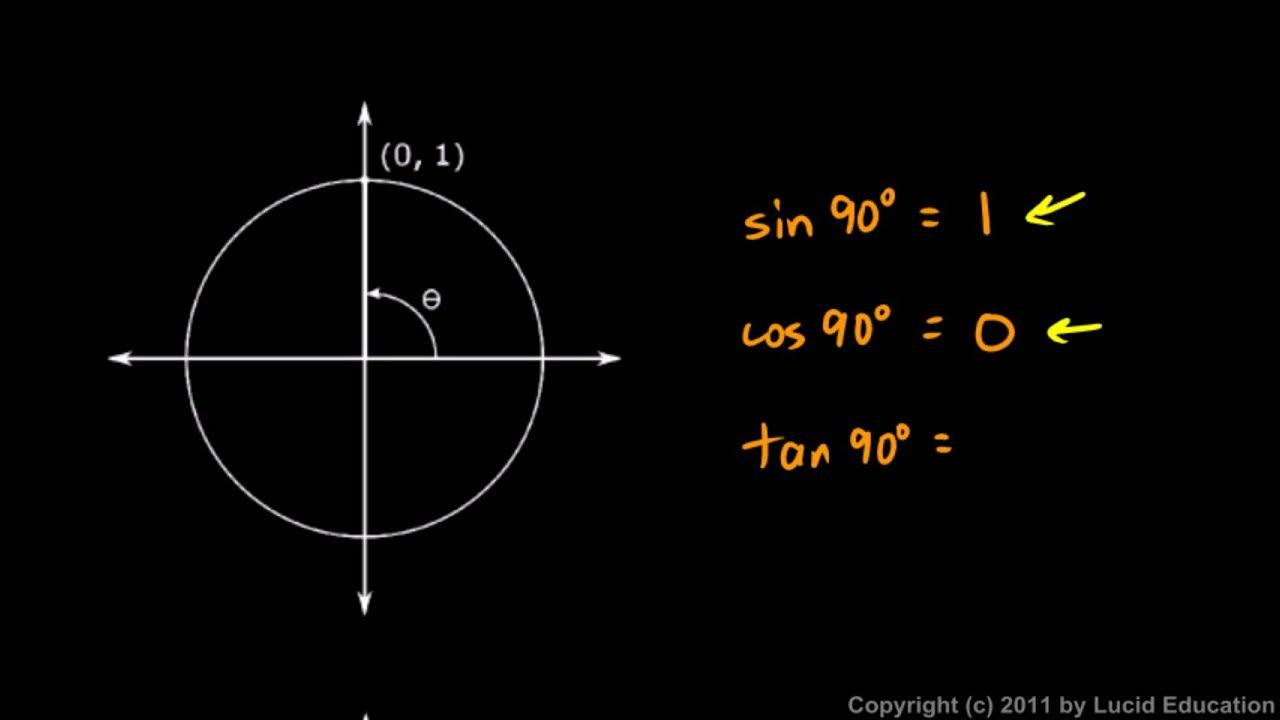
SUDUT BERELASI DALAM TRIGONOMETRI

Summary

This video provides an in-depth explanation of trigonometric relations within a circle, focusing on how to determine the values of sine, cosine, and tangent in different quadrants. It uses a mnemonic method to make memorizing trigonometric ratios easier, such as associating angles with the x-axis and leveraging quadrant-specific positivity rules. The presenter offers practical examples, guiding viewers on how to handle both positive and negative angles, and simplifies complex trigonometric calculations with clear steps. The video is designed to make learning trigonometry more intuitive and accessible.

Takeaways

• 😀 The script explains the concept of 'related angles' in a circle, emphasizing the relationship between angles and their positions on the coordinate plane.
• 😀 The quadrants are defined, with Quadrant 1 having all positive trigonometric ratios, Quadrant 2 having positive sine and cosecant, Quadrant 3 having positive tangent and cotangent, and Quadrant 4 having positive cosine and secant.
• 😀 A mnemonic for remembering trigonometric signs in different quadrants is introduced, referred to as 'Sindikat Tangan Kosong' (Empty Hand Syndicate).
• 😀 A clear explanation is given on how to find the values of trigonometric functions like sine, cosine, and tangent for different angles.
• 😀 For example, the value of cos 120° is found using the reference angle of 60° and the fact that cosine is negative in Quadrant 2.
• 😀 The process of finding sine, cosine, and tangent values involves referencing the closest axis (X or Y) and calculating the angle's difference from that axis.
• 😀 Practical examples are provided to illustrate how to compute values like sin 135° (using a reference angle of 45° in Quadrant 2) and tan 240° (with a reference angle of 60° in Quadrant 3).
• 😀 Negative angles are also discussed, explaining that negative angles rotate clockwise and their sign depends on the quadrant they land in.
• 😀 The importance of understanding quadrant-specific signs for trigonometric functions is emphasized to avoid confusion when solving problems.
• 😀 The script includes several example problems and solutions, highlighting how to approach angles in each quadrant and apply the correct trigonometric values for accurate results.

Q & A

What is meant by 'quadrants' in the unit circle?

Quadrants refer to the four sections of the unit circle, each representing a 90-degree range. These quadrants are numbered counterclockwise starting from the positive x-axis, and they help determine the sign of trigonometric functions like sine, cosine, and tangent in each section.

Which trigonometric functions are positive in the first quadrant?

In the first quadrant, all trigonometric functions—sine, cosine, and tangent—are positive.

How do you determine the sign of a trigonometric function in the second quadrant?

In the second quadrant, only sine and its reciprocal function cosecant are positive, while cosine, tangent, and their reciprocals are negative.

What is the pattern for determining the sign of trigonometric functions in the third quadrant?

In the third quadrant, only tangent and its reciprocal function cotangent are positive, while sine, cosine, and their reciprocals are negative.

What about the fourth quadrant? Which trigonometric functions are positive there?

In the fourth quadrant, cosine and its reciprocal function secant are positive, while sine, tangent, and their reciprocals are negative.

What is the mnemonic for remembering the signs of trigonometric functions in each quadrant?

The mnemonic 'All Students Take Calculus' helps remember that in the first quadrant, all functions are positive; in the second quadrant, only sine is positive; in the third quadrant, only tangent is positive; and in the fourth quadrant, only cosine is positive.

How do you calculate trigonometric functions for angles like 120°?

For 120°, which is in the second quadrant, you find the reference angle (180° - 120° = 60°). Since sine is positive in the second quadrant, you calculate sin(120°) by using sin(60°), which equals √3/2.

What is the method to solve for trigonometric functions of angles greater than 180°?

For angles greater than 180°, you first find the reference angle by subtracting the angle from 180° or 360°, depending on the quadrant. Then, apply the sign rule for the specific quadrant and calculate the corresponding trigonometric function.

How do you handle negative angles in the unit circle?

Negative angles are measured in the clockwise direction. To handle them, you treat them like positive angles but reverse the direction of rotation. The sign of the trigonometric function is determined by the quadrant in which the terminal side of the angle lies.

Can you explain how to calculate the value of cos(330°)?

To calculate cos(330°), which is in the fourth quadrant, first find the reference angle (360° - 330° = 30°). Since cosine is positive in the fourth quadrant, you use cos(30°), which equals √3/2. Therefore, cos(330°) = √3/2.