Materi Trigonometri
Summary
TLDRThis video provides a detailed explanation of trigonometry, focusing on right triangles, the Pythagorean theorem, and the fundamental trigonometric functions: sine, cosine, and tangent. It covers naming angles and sides, using Cartesian and polar coordinates, and calculating values for special angles (0°, 30°, 45°, 60°, 90°). The instructor also explains how angles behave in different quadrants, including reflections and adjustments, and emphasizes practical applications of these concepts. The lesson aims to build a strong foundation for understanding more advanced trigonometry, guiding learners step-by-step from basic principles to problem-solving using formulas and unit circle reasoning.
Takeaways
- 😀 Understanding trigonometry is essential for mastering upcoming chapters and advanced concepts.
- 😀 The Pythagorean theorem forms the foundation of right triangle trigonometry: a² + b² = c².
- 😀 Angles and sides are labeled differently depending on language or notation, e.g., English (A, B, C), Greek (α, β, γ).
- 😀 The sine function represents the ratio of the opposite side to the hypotenuse: sin α = opposite/hypotenuse.
- 😀 The cosine function represents the ratio of the adjacent side to the hypotenuse: cos α = adjacent/hypotenuse.
- 😀 The tangent function represents the ratio of the opposite side to the adjacent side: tan α = opposite/adjacent.
- 😀 Reciprocal functions include cosecant (csc), secant (sec), and cotangent (cot).
- 😀 Cartesian and polar coordinates can represent triangles, with x = r cos α and y = r sin α.
- 😀 Special angles like 0°, 30°, 45°, 60°, 90° have simple, derivable sine and cosine values without memorization.
- 😀 Angle transformations and reflections (e.g., sin(180°-α), cos(180°-α)) help handle triangles in different quadrants.
- 😀 Mastery of these fundamentals prepares students to tackle multiple formulas and more complex trigonometry applications.
Q & A
What foundational concept is essential before understanding trigonometry?
-The Pythagorean theorem is essential, which states that in a right triangle, the sum of the squares of the two shorter sides equals the square of the hypotenuse: a² + b² = c².
How are triangle vertices named in different languages?
-Triangle vertices can be labeled differently: in English as A, B, C; in Arabic as Alif, Ba, Ta; and in Greek as alpha (α), beta (β), gamma (γ), delta (δ).
What are the definitions of sine, cosine, and tangent in a right triangle?
-For a triangle with angle α: sin α = opposite/hypotenuse, cos α = adjacent/hypotenuse, tan α = opposite/adjacent.
What are the reciprocal trigonometric functions and their formulas?
-The reciprocals are: cosecant (csc α = 1/sin α), secant (sec α = 1/cos α), and cotangent (cot α = 1/tan α).
How are polar coordinates defined in relation to trigonometric functions?
-In polar coordinates, for a point with radius r and angle α: x = r * cos α, y = r * sin α. This helps relate Cartesian coordinates to angles.
What is the significance of the four quadrants in the Cartesian plane for trigonometry?
-Each quadrant affects the signs of sine and cosine: Quadrant I (+,+), Quadrant II (+,-), Quadrant III (-,-), Quadrant IV (-,+). This determines the value of trigonometric functions.
What are the special angles commonly used in trigonometry, and why are they important?
-Special angles are 0°, 30°, 45°, 60°, 90°. They are important because their sine and cosine values can be derived using simple fractions and square roots, facilitating calculations without memorization.
How does the reflection of triangles across axes affect trigonometric functions?
-Reflection changes the angle positions: for example, sin(180° - α) = sin α, cos(180° - α) = -cos α, and sin(360° - α) = -sin α. These transformations help solve trigonometric problems in different quadrants.
What is the relationship between the angle and its opposite side in a right triangle?
-The angle determines which side is considered opposite. For angle α, the opposite side is labeled as 'a' and lies directly across from α. This relationship is used in defining sine and tangent.
Why is understanding trigonometric relationships in right triangles important for future lessons?
-Understanding these relationships allows students to solve more complex problems involving multiple triangles, polar coordinates, and angle transformations, forming the foundation for 54 formulas in upcoming chapters.
How are sine, cosine, and tangent values calculated for special angles like 30°, 45°, and 60°?
-For 30°: sin 30° = 1/2, cos 30° = √3/2; for 45°: sin 45° = √2/2, cos 45° = √2/2; for 60°: sin 60° = √3/2, cos 60° = 1/2. These values can be derived using the unit circle or triangle ratios.
What method is suggested to easily remember sine values for special angles?
-The speaker suggests using a sequence with square roots: take 0, 1, 2, 3, 4, divide each by 2, and take the square root for sine values. This avoids memorization and allows quick calculation.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

TRIGONOMETRI - Ukuran Sudut dan Perbandingan Trigonometri

Basic trigonometry II | Basic trigonometry | Trigonometry | Khan Academy

Menentukan Nilai Trigonometri Segitiga Siku Siku Perbandingan Trigonometri segitiga Siku Siku

Trigonometry For Beginners!

Pembahasan Soal Latihan Mandiri Trigonometri Dasar Matematika Wajib Kelas X
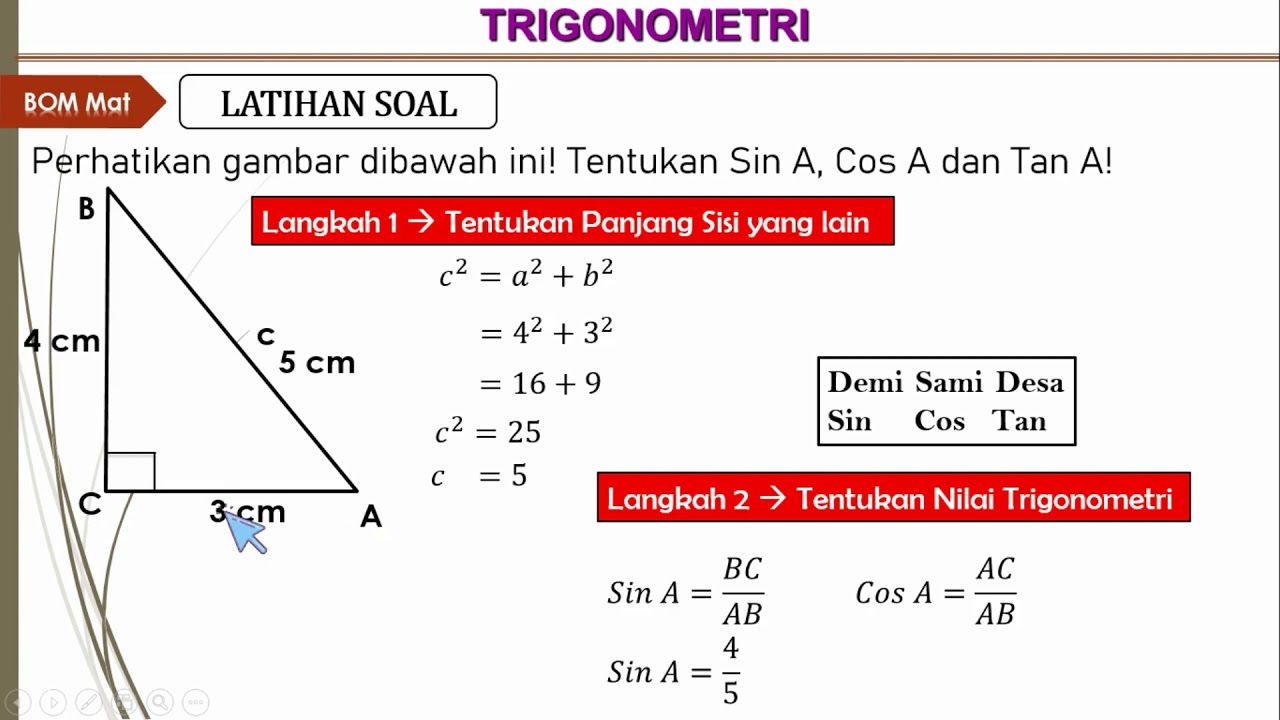
Perbandingan trigonometri pada segitiga siku siku, Menjelaskan rasio trigonometri
5.0 / 5 (0 votes)