Calculo integral
Summary
TLDREste video ofrece una introducción al cálculo integral, explicando su importancia en matemáticas, ciencia e ingeniería. Se aborda la historia de la integración desde el Antiguo Egipto hasta la formulación del teorema fundamental del cálculo por Newton y Leibniz. El concepto de integral se explora como una generalización de la suma de infinitos elementos pequeños, y se explica cómo la integración permite calcular áreas y volúmenes, entre otros. También se menciona la evolución del cálculo integral a lo largo de los siglos, destacando los avances que llevaron a las definiciones modernas y sus aplicaciones prácticas.
Takeaways
- 😀 La integración es un concepto fundamental del cálculo y del análisis matemático, representando una generalización de la suma de infinitos sumandos infinitesimalmente pequeños.
- 😀 La integral es la operación inversa al diferencial de una función y tiene aplicaciones cruciales en áreas como la ingeniería, ciencia y cálculo de áreas y volúmenes.
- 😀 El teorema fundamental del cálculo, desarrollado por Isaac Newton y Gottfried Wilhelm Leibniz, establece que la derivación y la integración son procesos inversos.
- 😀 Existen dos tipos principales de integrales: las indefinidas y las definidas, siendo las definidas más utilizadas en aplicaciones prácticas.
- 😀 Los principios de la integración fueron formulados por Newton y Leibniz a finales del siglo XVII, estableciendo una conexión entre derivación e integración.
- 😀 A lo largo de la historia, la integración se ha utilizado para calcular áreas y volúmenes, y ha sido desarrollada por matemáticos de distintas culturas como los egipcios, griegos y chinos.
- 😀 El cálculo infinitesimal, desarrollado por Newton y Leibniz, permite analizar funciones con dominios continuos, estableciendo una base matemática robusta para la integración.
- 😀 La teoría moderna de la integración se basa en la integral de Riemann, que fue formulada utilizando límites y se convirtió en una herramienta clave en el cálculo.
- 😀 Las integrales también tienen aplicaciones en la física, como en la formulación de leyes relacionadas con el electromagnetismo y otros campos de la ciencia.
- 😀 En el siglo XX, la teoría de la integración evolucionó para incluir la integral de Lebesgue y otros avances relacionados con la probabilidad y el cálculo cuántico, ampliando su aplicación y rigor.
Q & A
¿Qué es la integración en matemáticas?
-La integración es un concepto fundamental en el cálculo y análisis matemático. Es la generalización de la suma de infinitos sumandos infinitesimalmente pequeños, lo que permite calcular áreas, volúmenes y otros valores en diversas aplicaciones de la ciencia y la ingeniería.
¿Cuál es la relación entre la derivación y la integración?
-La derivación y la integración son procesos inversos. El teorema fundamental del cálculo establece que ambos están conectados, y una antiderivada puede calcularse a partir de una derivada, y viceversa.
¿Quiénes fueron los principales matemáticos involucrados en el desarrollo de la integración?
-René Descartes, Isaac Newton, y Gottfried Wilhelm Leibniz fueron figuras clave en el desarrollo de la integración. Sus trabajos contribuyeron al teorema fundamental del cálculo y a la formulación de las bases del cálculo infinitesimal.
¿Qué es una integral indefinida?
-Una integral indefinida es aquella que no tiene límites específicos en sus valores de integración y se refiere a la primitiva de una función, es decir, la función cuya derivada es la función original.
¿Qué se entiende por integral definida?
-La integral definida se refiere a la operación matemática que calcula el valor exacto del área bajo una curva entre dos puntos específicos. Es un caso particular de la integración que involucra límites definidos.
¿Cómo contribuyó la antigua civilización egipcia al desarrollo de la integración?
-Los egipcios ya utilizaban una fórmula para calcular el volumen de un tronco piramidal alrededor del 1800 a.C., lo que muestra que tenían conocimientos rudimentarios sobre la integración, al menos en términos de geometría.
¿Qué métodos utilizaron matemáticos antiguos como Arquímides en el desarrollo de la integración?
-Arquímides usó un método que se basaba en la aproximación de áreas y volúmenes dividiendo las figuras en infinitos trozos pequeños. Este enfoque fue un precursor de las técnicas modernas de integración.
¿En qué consistía el método de excepción de Éxodo en el cálculo integral?
-El método de excepción de Éxodo, desarrollado alrededor del 370 a.C., trataba de encontrar áreas y volúmenes mediante la división en pequeños fragmentos, similar al proceso de integración, lo que fue un avance temprano en las matemáticas.
¿Qué aportes significativos trajeron Newton y Leibniz al cálculo integral?
-Newton y Leibniz formularon el teorema fundamental del cálculo, que establece que la derivación y la integración son procesos inversos, y crearon el cálculo infinitesimal, que facilitó la resolución de una amplia gama de problemas matemáticos y físicos.
¿Cómo evolucionó la noción de integral en el siglo XIX?
-En el siglo XIX, la noción de integral se formalizó con el desarrollo de la teoría de los límites por Cauchy y la rigorosidad del concepto de integral de Riemann, lo que permitió una definición matemática más precisa y general de la integración.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

ESTO es lo que NECESITAS SABER de CALCULO I ⌚▶FUNCIONES, LIMITES, DERIVADAS E INTEGRALES
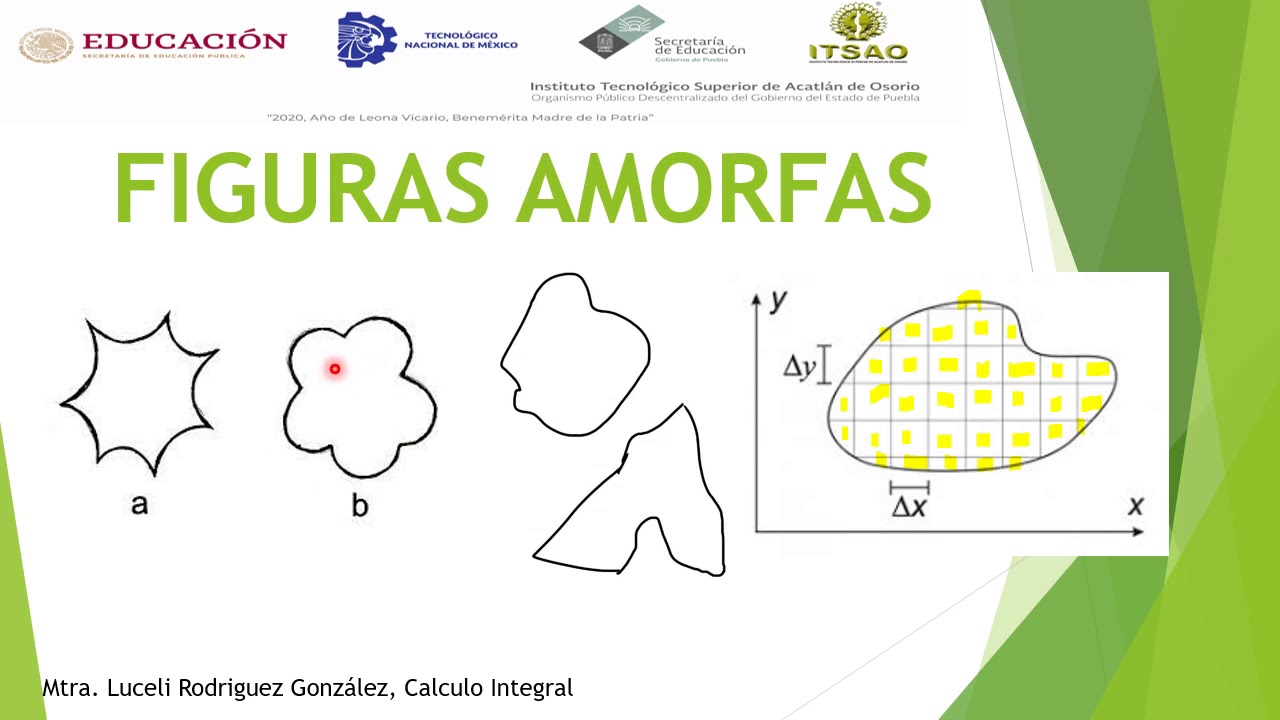
Figuras amorfas y notación sumatoria

Qué es la integral y Para qué se usa

Cálculo Infinitesimal - Conceptos, aplicaciones y ejercicios

INTEGRALES - Clase Completa desde cero

Cálculo de variación: Construcción histórica.
5.0 / 5 (0 votes)
