GARIS DAN SUDUT (PART 1)
Summary
TLDRThis educational video by Rozi provides a thorough explanation of lines and angles, a key topic for middle school students. It covers various aspects such as types of angles (acute, obtuse, right, and reflex), how to measure angles using a protractor, and relationships between angles like supplementary, complementary, and vertically opposite angles. The video is tailored to help students, especially those in grades 7-9, with their understanding of geometric concepts in preparation for exams. Practical examples, exercises, and problem-solving techniques are also included for better comprehension.
Takeaways
- 😀 The lesson focuses on lines and angles, a topic typically introduced in Grade 7 but also relevant for Grade 9 students preparing for national exams.
- 😀 Real-world examples, such as the angles found in houses, are used to make the topic relatable and easy to understand.
- 😀 The script introduces the components of an angle, including the arms and the vertex, and explains how to measure angles using a protractor.
- 😀 The angle is labeled as 'ABC,' and it is explained that the middle letter represents the vertex, which is crucial for naming angles correctly.
- 😀 The script explains how to measure angles between 0° and 180°, using both the top and bottom scales of the protractor depending on the direction of measurement.
- 😀 Types of angles are introduced, including acute angles (between 0° and 90°), obtuse angles (between 90° and 180°), right angles (exactly 90°), and reflex angles (between 180° and 360°).
- 😀 The importance of correctly identifying the type of angle is emphasized through visual examples of each angle type.
- 😀 The relationship between angles is discussed, covering supplementary angles (sum of 180°), complementary angles (sum of 90°), and vertically opposite angles (which are equal).
- 😀 The script provides examples of angle relationships, such as the sum of supplementary angles being 180° and complementary angles adding up to 90°.
- 😀 Practice problems are given to reinforce the concepts, such as calculating supplementary and complementary angles and solving for unknown angles using algebraic equations.
- 😀 The lesson concludes by promising a follow-up discussion on parallel lines and their relationship to angles in a future lesson.
Q & A
What are the three components of an angle?
-The three components of an angle are the vertex, the arms (or legs) of the angle, and the angle itself. The vertex is the point where the two lines meet, while the arms are the two lines that form the angle.
What is the difference between an acute angle and an obtuse angle?
-An acute angle is an angle that measures less than 90°, while an obtuse angle measures between 90° and 180°.
How do you measure an angle using a protractor?
-To measure an angle using a protractor, you align one leg of the angle with the baseline of the protractor, ensuring the vertex matches the center of the protractor. Depending on the direction of the angle, you read the measurement from the top or bottom scale of the protractor.
What is the difference between supplementary and complementary angles?
-Supplementary angles are two angles that add up to 180°, while complementary angles are two angles that add up to 90°.
What does the term 'vertical angles' refer to?
-Vertical angles are the angles formed when two lines intersect. They are always equal to each other and are opposite in position.
What is the measurement of a right angle?
-A right angle is exactly 90°.
How would you find the reflex angle between two lines?
-A reflex angle is an angle that measures between 180° and 360°. To find it, you subtract the smaller angle from 360°.
What is an example of a reflex angle in real life?
-An example of a reflex angle is the large angle between the hands of a clock at 10:10, where the angle is more than 180°.
How do you calculate the supplementary angle of 85°?
-To calculate the supplementary angle of 85°, you subtract it from 180°: 180° - 85° = 95°.
What is the complementary angle of 28°?
-The complementary angle of 28° is found by subtracting it from 90°: 90° - 28° = 62°.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
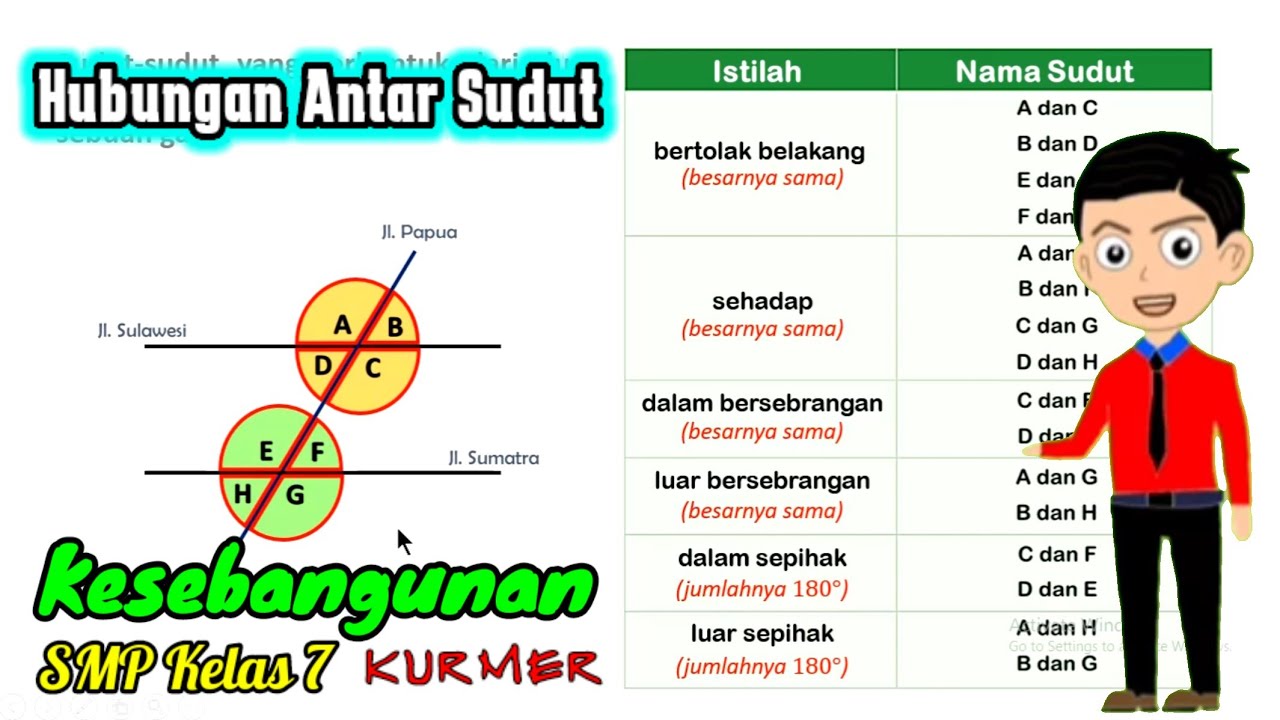
kesebangunan bagian 1 (hubungan antar sudut)

Kurikulum Merdeka Materi Matematika Kelas 7 Bab 5 Kesebangunan

Aula 03 - Reflexão da Luz

Segi Empat (1) | Persegi dan Persegi Panjang | Matematika Kelas 7

Pembahasan Mari Kita Periksa Garis Sejajar dan Segi Banyak Hal 115 Bab 4 Kelas 8 Kurikulum Merdeka
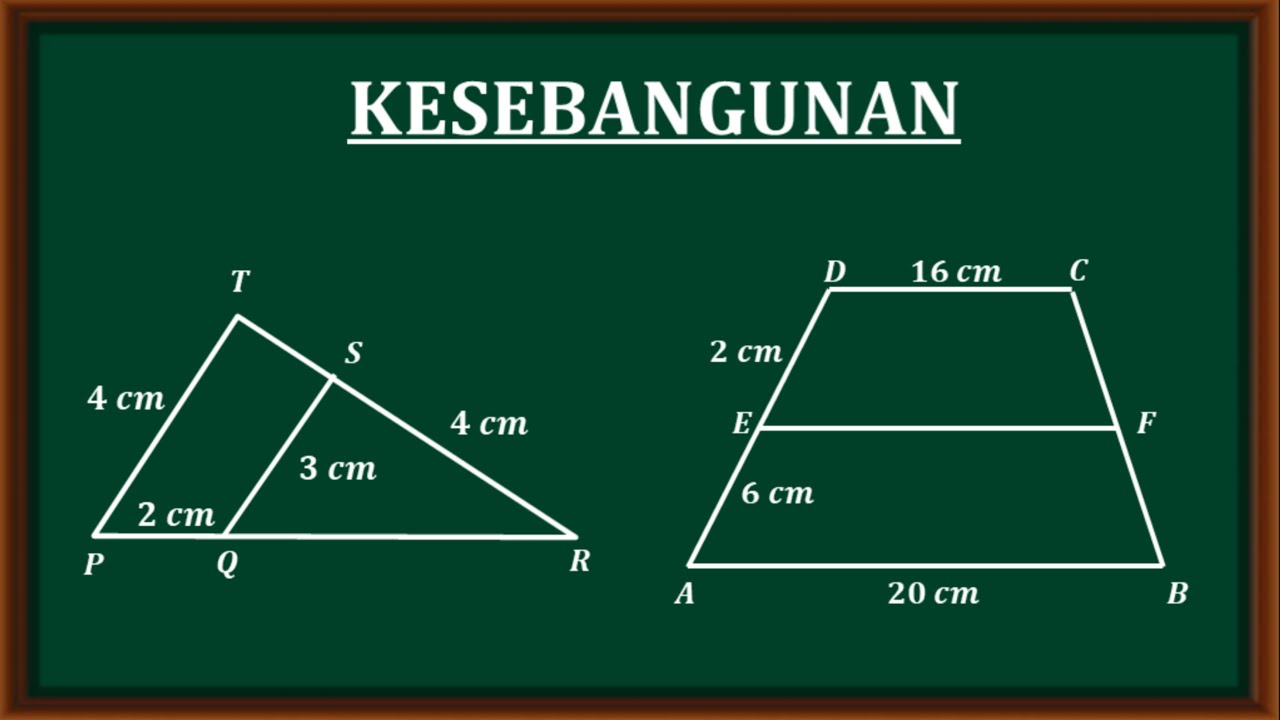
Kesebangunan - soal dan pembahasan materi kesebangunan matematika tingkat SMP kelas ix
5.0 / 5 (0 votes)
