Spherical Geometry in Navigation

Summary

This video explains the concept of spherical geometry and its relevance to navigation, particularly air travel. It explores the differences between spherical and Euclidean geometry, emphasizing how great circles, rather than straight lines, represent the shortest paths on a sphere. The video illustrates how flight paths, such as from Florida to the Philippines, often follow these great circles, which may appear counterintuitive but are the most efficient routes. The content provides a compelling, accessible introduction to how geometry influences the real-world application of air travel and navigation.

Takeaways

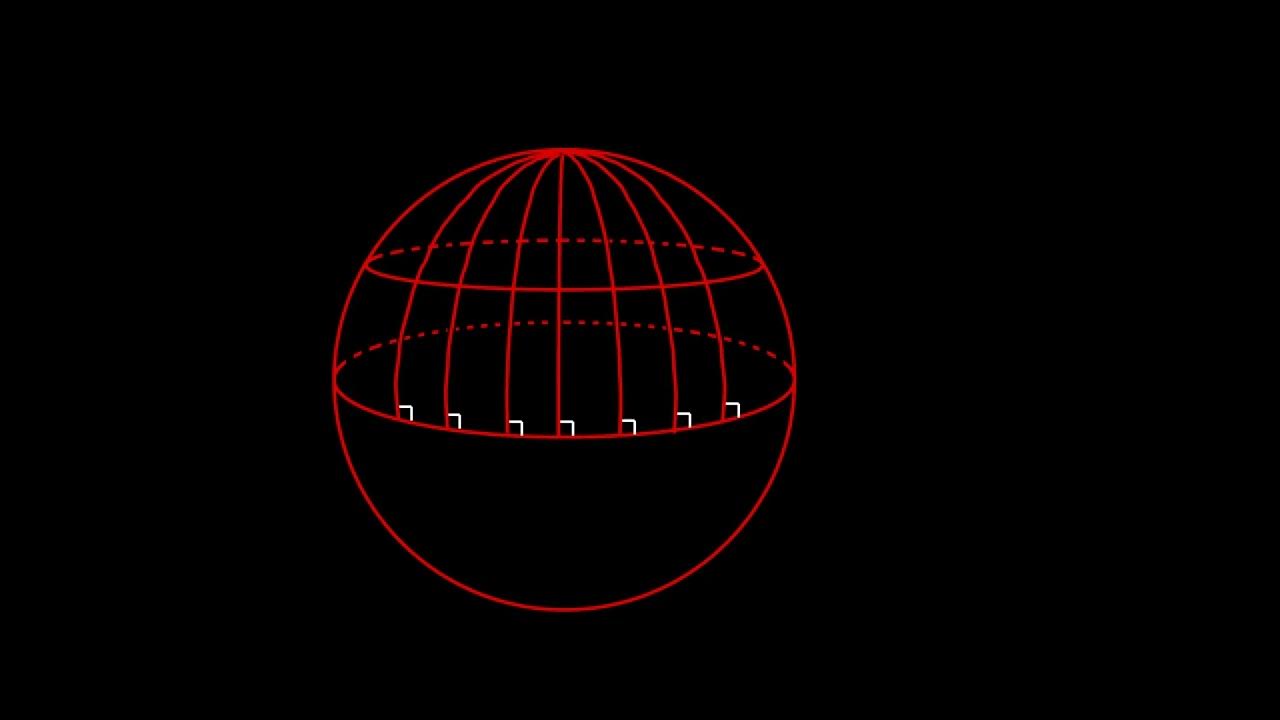
• 😀 Spherical geometry is the study of two-dimensional geometry on the surface of a sphere.
• 😀 The shortest path between two points on a sphere is along a great circle, not a straight line on a flat map.
• 😀 Great circles are the largest possible circles that can be drawn on a sphere, and they divide the sphere into two equal hemispheres.
• 😀 In spherical geometry, straight lines are considered great circles, even though they appear curved due to the sphere's surface.
• 😀 Unlike Euclidean geometry, there are no parallel lines in spherical geometry—two distinct great circles always intersect at two points.
• 😀 Triangles in spherical geometry can have a sum of interior angles greater than 180 degrees, unlike Euclidean triangles.
• 😀 A triangle with three right angles is possible in spherical geometry, which would be impossible in flat geometry.
• 😀 Spherical geometry challenges the typical Euclidean understanding, especially in terms of navigation and projection onto a 2D plane.
• 😀 Airplanes take flight paths that follow great circles, even if those routes appear unusual when plotted on a flat map.
• 😀 The flight path from Florida to the Philippines, for example, follows a great circle that passes through Alaska, rather than a straight line on a map.

Q & A

What is spherical geometry?

Spherical geometry is a type of non-Euclidean geometry that deals with shapes on the surface of a sphere. It involves concepts like great circles and the properties of triangles on a spherical surface.

How does spherical geometry differ from Euclidean geometry?

While Euclidean geometry applies to flat surfaces, spherical geometry deals with curved surfaces, like the surface of a sphere. Key differences include the behavior of straight lines (great circles on a sphere) and the absence of parallel lines in spherical geometry.

What is a great circle in spherical geometry?

A great circle is the intersection of a sphere with a plane that passes through the center of the sphere. It divides the sphere into two equal hemispheres and is considered the spherical equivalent of a straight line.

Why are great circles important in navigation?

Great circles represent the shortest path between two points on the surface of a sphere, which is why airplanes often follow great circle routes when traveling long distances on Earth.

How do great circles relate to air travel?

In air travel, the shortest flight path between two locations follows a great circle. This explains why some flight paths, like those from Florida to the Philippines, may appear to curve or deviate from a direct route.

Why do spherical geometry triangles have angles that sum to more than 180 degrees?

In spherical geometry, triangles are formed by the intersection of three great circles. Due to the curvature of the sphere, the sum of the interior angles of a triangle can exceed 180 degrees, unlike in Euclidean geometry.

What are antipodal points in spherical geometry?

Antipodal points are two points on the surface of a sphere that are directly opposite each other, the farthest distance apart that can be achieved on a sphere.

What is the Euclidean postulate that does not hold in spherical geometry?

Euclid's fifth postulate, which states that parallel lines do not intersect, does not hold in spherical geometry. In spherical geometry, any two distinct great circles will intersect at two points.

Why do planes often fly routes that seem indirect, such as over Alaska when traveling from Florida to the Philippines?

The flight path follows the great circle route, which is the shortest distance between the two locations. Although the path may seem indirect on a flat map, it is actually the most efficient route on the curved surface of the Earth.

What is the significance of the equator in spherical geometry?

The equator is the only latitude that is a great circle, meaning it divides the Earth into two equal hemispheres and has the same radius as the Earth itself, unlike other latitudes that are smaller circles.