Área de figuras básicas
Summary
TLDREl video ofrece una explicación clara y detallada sobre el cálculo del área de diversas figuras geométricas, comenzando con el cuadrado y avanzando hacia el rectángulo, paralelogramo, triángulo, rombo y trapecio. Se utilizan ejemplos visuales para ilustrar cómo se determina el área, enfatizando la relación entre las dimensiones y el área total. A través de la rotación y descomposición de figuras, se muestra cómo calcular áreas con fórmulas específicas, permitiendo a los espectadores comprender de manera efectiva los conceptos geométricos y su aplicación en problemas matemáticos.
Takeaways
- 📐 Un cuadrado con un lado de 1 unidad tiene un área de 1 unidad cuadrada.
- 📏 Un cuadrado de 2 unidades de lado cubre 4 cuadrados de 1 unidad, por lo que su área es 4 unidades cuadradas.
- 🔺 Un cuadrado de 3 unidades de lado cubre 9 cuadrados de 1 unidad, resultando en un área de 9 unidades cuadradas.
- 🔢 En general, el área de un cuadrado de lado l es igual a l al cuadrado unidades cuadradas.
- 📊 El área de un rectángulo se calcula multiplicando su base b por su altura h (A = b * h).
- 🔲 El área de un paralelogramo es igual a la base b por la altura h (A = b * h).
- 🔻 El área de un triángulo se puede encontrar como la mitad del área de un paralelogramo (A = b * h / 2).
- 🔷 Un rombo se puede descomponer en cuatro triángulos rectángulos congruentes, y su área es 4 veces el área de un triángulo (A = 4 * (1/2 * b * h)).
- 🔼 Un trapecio tiene un área que es la mitad del área de un paralelogramo formado por dos trapecios congruentes.
- 📐 El área del trapecio se calcula como (B mayor + B menor) * h / 2, donde B mayor y B menor son las longitudes de las bases.
Q & A
¿Cuál es el área de un cuadrado con un lado de 2 unidades?
-El área de un cuadrado se calcula como el cuadrado de su lado. Por lo tanto, el área es 2^2 = 4 unidades cuadradas.
¿Cómo se calcula el área de un rectángulo?
-El área de un rectángulo se calcula multiplicando su base por su altura. Si la base es b y la altura es h, el área es A = b × h.
¿Cuál es la relación entre el área de un paralelogramo y un rectángulo?
-El área de un paralelogramo también se calcula como base por altura (A = b × h), y se puede demostrar que su área es equivalente a la de un rectángulo con la misma base y altura.
¿Qué método se utiliza para encontrar el área de un triángulo?
-El área de un triángulo se calcula como la mitad del producto de su base y altura, es decir, A = (b × h) / 2.
¿Cómo se determina el área de un rombo?
-El área de un rombo se puede encontrar descomponiéndolo en cuatro triángulos rectángulos congruentes o utilizando la fórmula A = (d_1 × d_2) / 2, donde d_1 y d_2 son las longitudes de las diagonales.
¿Qué fórmula se usa para calcular el área de un trapecio?
-El área de un trapecio se calcula como A = ((B_{mayúscula} + B_{mínuscula}) × h) / 2, donde B_{mayúscula} y B_{mínuscula} son las longitudes de las bases y h es la altura.
¿Por qué el área de un triángulo es la mitad de la de un paralelogramo?
-Porque al rotar un triángulo sobre su base, se forma un paralelogramo, lo que implica que el área del triángulo es la mitad del área del paralelogramo formado.
¿Cuántos triángulos congruentes se pueden formar al dividir un rombo?
-Un rombo puede ser dividido en cuatro triángulos rectángulos congruentes.
¿Qué se puede deducir sobre el área de un trapecio usando su rotación?
-Al rotar un trapecio, se forma un paralelogramo del que se puede deducir que el área del trapecio es la mitad del área de ese paralelogramo.
¿Cómo se relacionan las áreas de figuras geométricas en este contexto?
-Las áreas de las figuras geométricas están interrelacionadas a través de sus fórmulas, y muchas pueden ser deducidas a partir de otras figuras, como se muestra al comparar triángulos, paralelogramos y trapezoides.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Troncho y Poncho: Áreas de polígonos

Pensamiento Matemático II PROGRESION 9

ÁREA DE TODAS LAS FIGURAS Super facil Para principiantes

Producto vectorial bajo la luz de las transformaciones lineales | Álgebra lineal, capítulo 8b
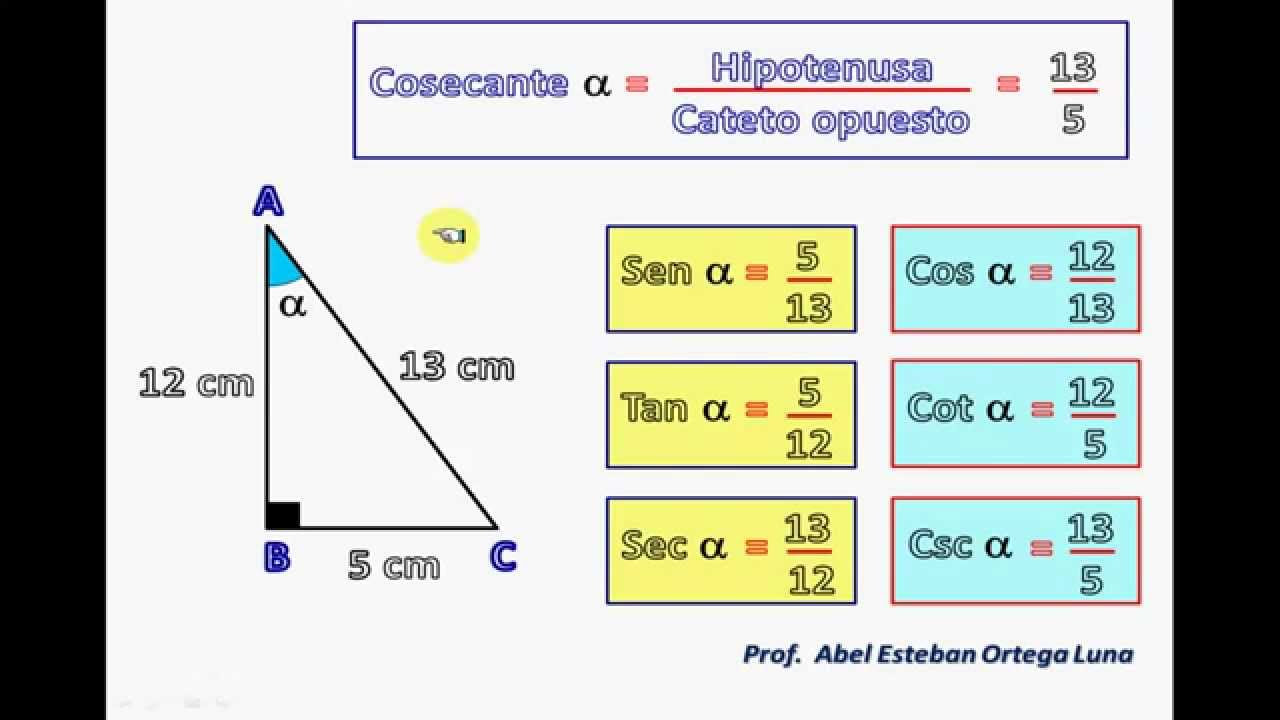
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO
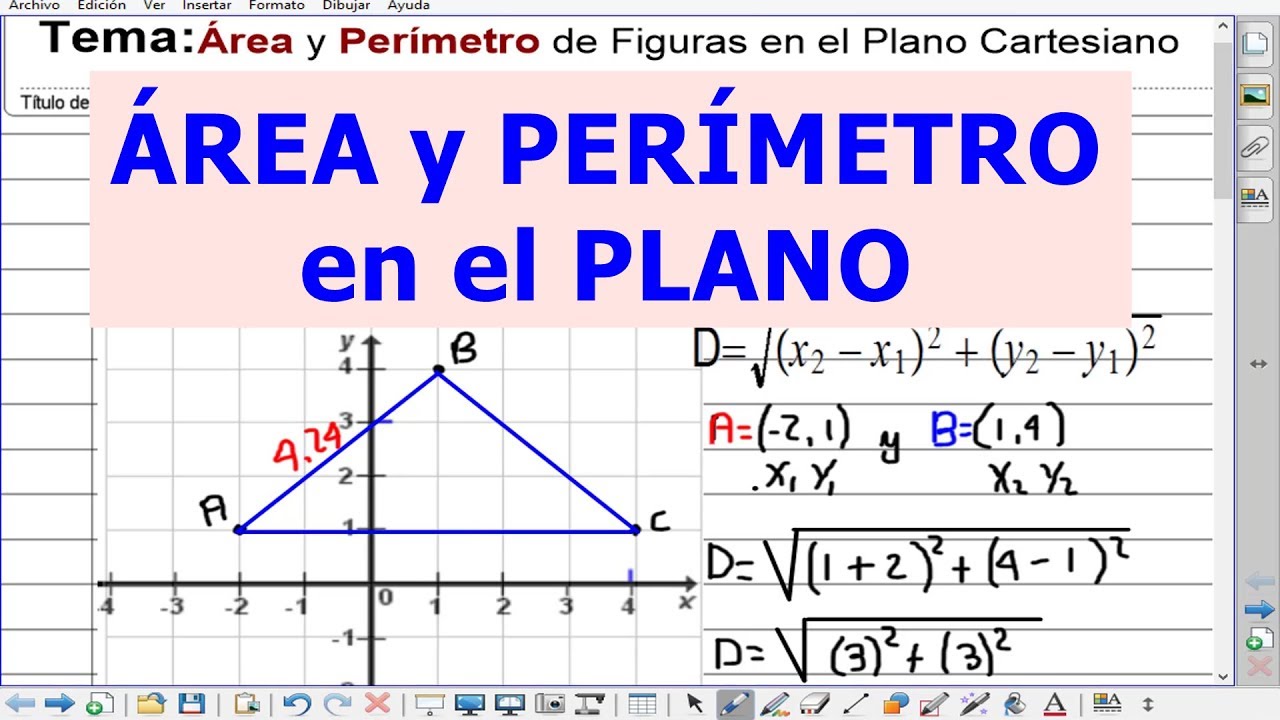
Área y Perímetro de Figuras en el Plano Cartesiano.
5.0 / 5 (0 votes)
