Zeros de funções Método Iterativo Linear

Summary

In this video, various methods for finding the roots of functions are discussed, including linear iterative, fixed-point, and secant methods. Initially, it covers bisection as a root-finding approach and then introduces fixed-point methods, which are more efficient. By restructuring the equation into iterative functions, roots are found using successive approximations. An example with a quadratic equation is explored to illustrate the process and potential convergence issues. The video also explains how to verify convergence through conditions on the derivative and how non-converging cases differ, emphasizing the importance of checking these conditions before using iterative methods.

Takeaways

• 🔍 The lesson introduces three iterative methods for finding function zeros: Fixed Point, Newton's method, and Secant method.
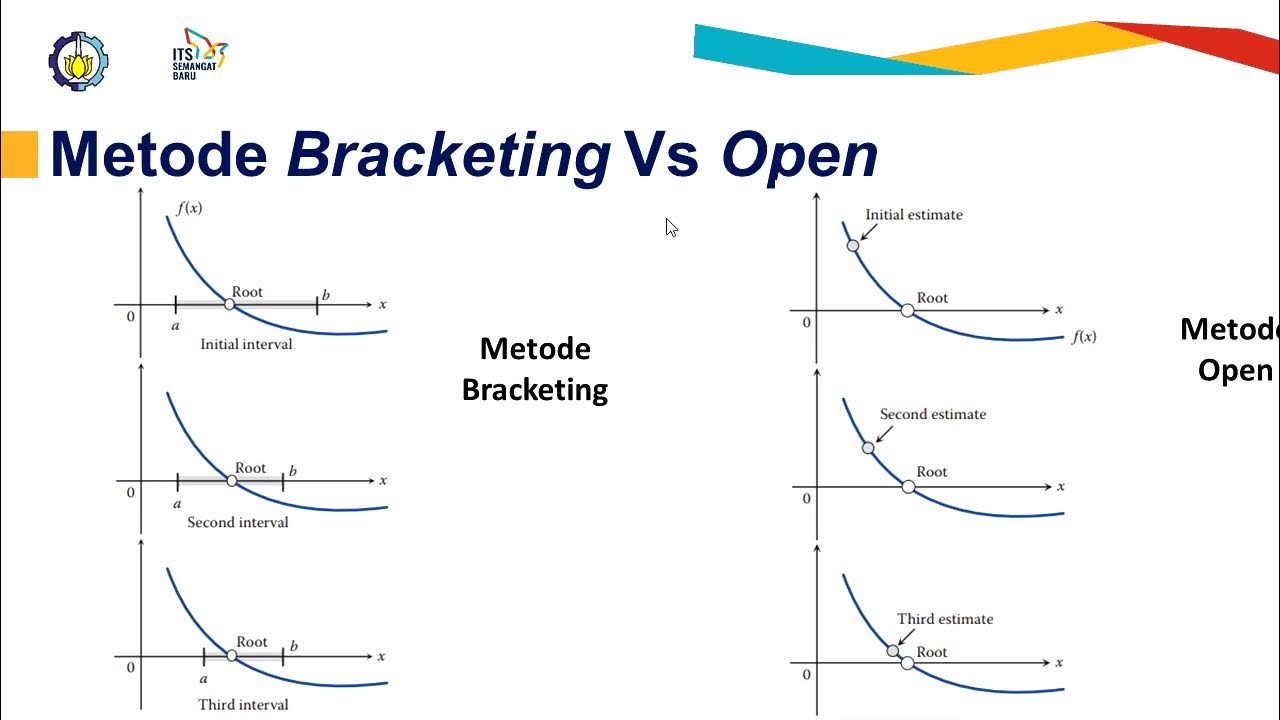
• ⚖️ Earlier, the Bisection method was discussed, where interval-based sign changes helped find roots.
• 🔗 The Fixed Point method rewrites the function f(x) in a way that f(x) equals x and iterates to find roots.
• 💡 For example, f(x) = x^2 + x - 6 can be solved by isolating x, turning the equation into x = sqrt(6 - x).
• 📉 Starting with an initial guess, the process iterates by calculating new x-values until it converges to a root.
• 🔄 Iterations involve substituting values back into the equation until the solution stabilizes.
• ⚠️ However, the method is not always reliable. A wrong initial guess or function form may lead to divergence.
• 🧮 The method relies on checking convergence conditions, such as ensuring the derivative of the iteration function is less than 1 in the given interval.
• 📈 An example using x = sqrt(6 - x) shows convergence, while another example with x = 6 - x^2 shows divergence.
• 📝 Convergence depends on specific conditions: the function and its derivative must be continuous, and the derivative's magnitude must be less than 1 in the interval.

Q & A

What is the main goal of the fixed-point iteration method discussed in the script?

The main goal of the fixed-point iteration method is to find the root of a function by rewriting it in a form where the function's value is equal to its input, i.e., f(x) = x.

How does the fixed-point iteration method differ from methods like bisection?

Unlike bisection, which divides an interval to find a sign change indicating a root, the fixed-point iteration method focuses on transforming the equation into a form where f(x) = x and iterating to find where the function converges to the root.

What initial step is necessary for applying the fixed-point iteration method?

The initial step is to isolate x in the given function f(x), rewriting the equation in the form x = g(x), where g(x) is the new function derived from f(x).

What is the key criterion for the fixed-point iteration method to work successfully?

The method works if the function and its derivative are continuous in the given interval, and the derivative of the function is less than 1 in absolute value throughout the interval. This ensures the convergence of the method.

Why did the example function f(x) = 6 - x² fail in the fixed-point iteration method?

The function f(x) = 6 - x² failed because its derivative did not satisfy the convergence condition in the given interval. Specifically, the derivative was not less than 1 in absolute value across the interval that includes the root.

What conditions must be checked before applying the fixed-point iteration method?

Before applying the fixed-point iteration method, one must check that the function and its derivative are continuous over the interval and that the absolute value of the derivative is less than 1 in that interval to ensure convergence.

What example is provided in the script to demonstrate a successful application of the method?

An example using the function f(x) = √(6 - x) is provided, where the method successfully converges to the root x = 2, as the conditions for convergence are met.

How is the next iteration value calculated in the fixed-point iteration method?

The next iteration value is calculated by substituting the current approximation of x into the function g(x). For example, x₁ = √(6 - x₀), where x₀ is the initial guess.

What happens if the convergence conditions are not satisfied in the fixed-point iteration method?

If the convergence conditions are not satisfied, the method will not work correctly, and instead of converging to a root, the iterations will diverge, meaning the values of x will move further away from the actual root.

What is the significance of checking the derivative when applying the fixed-point method?

Checking the derivative is crucial because it ensures that the iterations will converge. If the absolute value of the derivative is greater than 1, the iterations will diverge, making the method fail to find the root.