METODE NUMERIK P7 PART 1/2 | METODE NEWTON-RAPHSON UNTUK MENYELESAIKAN PERSAMAAN NON LINIER

Summary

In this video lecture, Fitria Zona Kumala introduces the Newton-Raphson method for solving non-linear equations in numerical methods. The lecture explains the iterative process of finding roots, using an example equation to demonstrate the method’s application. Key points include the importance of selecting an appropriate initial guess and checking conditions like the derivative not being zero. The lecture walks through step-by-step calculations, showing how convergence occurs and the method’s efficiency in finding roots quickly compared to other methods. The session concludes with a practical application of the Newton-Raphson method and the final result of a root approximation.

Takeaways

• 😀 The lecture discusses the Newton-Raphson method for solving nonlinear equations.
• 😀 The Newton-Raphson method is favored for its fast convergence compared to other root-finding methods.
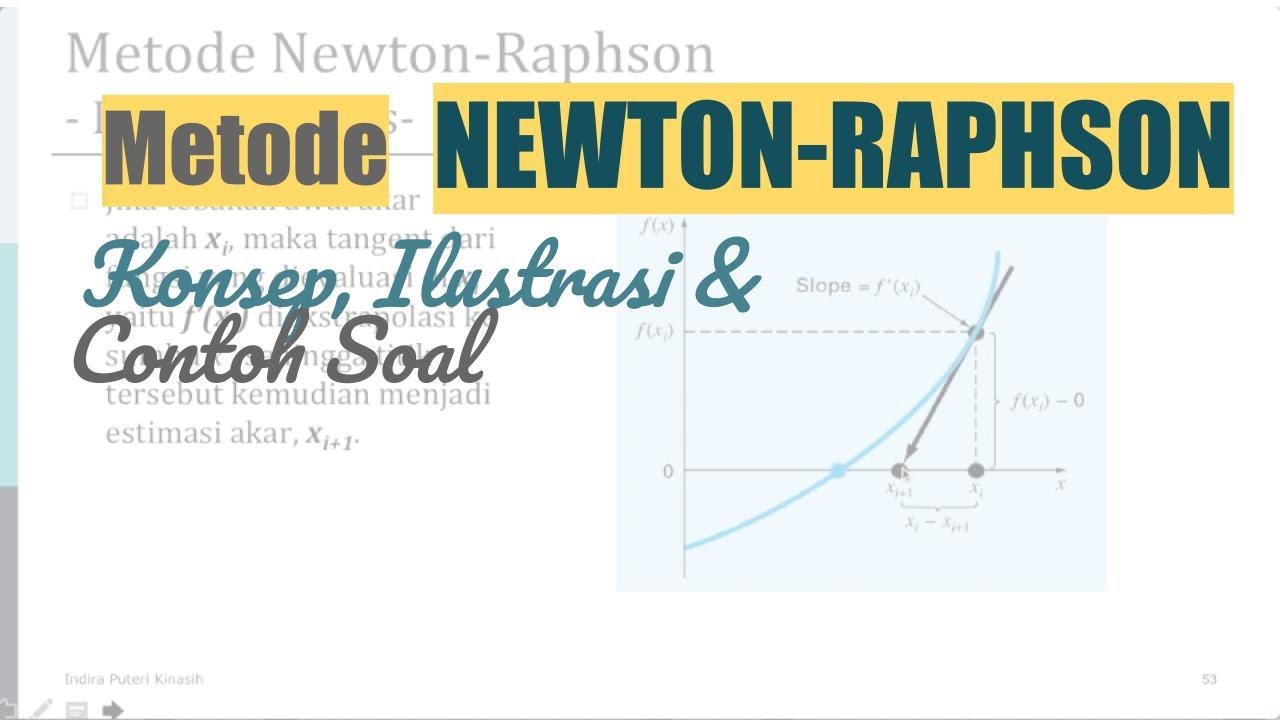
• 😀 The iterative formula for the Newton-Raphson method is: Xr+1 = Xr - (f(Xr) / f'(Xr)).
• 😀 The iteration stops when the absolute difference between successive values of Xr is smaller than a predefined epsilon (0.000001 in this case).
• 😀 If the derivative (f'(Xr)) equals zero, the method is restarted with a new initial guess (X0).
• 😀 The method is sensitive to the initial guess, as different guesses can lead to convergence to different roots.
• 😀 A practical example was shown to solve the equation f(x) = x^x - x - 2 using the Newton-Raphson method with an initial guess of X0 = 5.
• 😀 The function to solve was f(x) = e^x - x - 2, and its derivative is f'(x) = e^x - 1.
• 😀 The solution process involves calculating f(Xr), f'(Xr), and updating Xr iteratively until the stopping condition (epsilon) is met.
• 😀 The final root approximation after 10 iterations was found to be approximately 1.146193, which is the root of the given nonlinear equation.

Q & A

What is the main focus of the script?

The script discusses the Newton-Raphson method for solving nonlinear equations in a numerical methods course.

What is the Newton-Raphson method known for in numerical methods?

The Newton-Raphson method is known for its fast convergence rate compared to other root-finding methods, making it widely used in applied science and engineering.

What is the iteration formula for the Newton-Raphson method?

The iteration formula is given by X_(n+1) = X_n - (f(X_n) / f'(X_n)), where f(X_n) is the function value at X_n and f'(X_n) is the derivative of the function at X_n.

What condition must be met for the Newton-Raphson method to continue iterating?

The iteration stops when the absolute difference between the values of X_(n+1) and X_n is smaller than a predefined threshold, epsilon.

What happens if the derivative of the function at X_n is zero in the Newton-Raphson method?

If the derivative is zero, the iteration must be restarted with a different initial guess for X_0, as division by zero would occur.

What is the initial guess for the root in the provided example?

In the example, the initial guess for the root is X_0 = 5.

What was the function used in the example to find the root?

The function used in the example is f(x) = e^x - x - 2.

How do you calculate the derivative of the function f(x) = e^x - x - 2?

The derivative of the function is f'(x) = e^x - 1, as the derivative of e^x is e^x and the derivatives of -x and -2 are -1 and 0, respectively.

What criteria must the values of the iteration satisfy to stop the Newton-Raphson method?

The iteration stops when the absolute value of the difference between successive approximations is smaller than epsilon (0.000001 in the example).

What was the final approximation of the root obtained in the example after 10 iterations?

After 10 iterations, the final approximation of the root was 1.146193.