03. Raíz sexta de 2, resuelta por método de Newton Raphson
Summary
TLDREste vídeo enseña cómo calcular la raíz sexta de 2 con precisión de 8 decimales usando el método de Newton-Raphson. Se explica el proceso paso a paso, comenzando con la función f(x) = x^6 - 2 y buscando el valor de x que haga que f(x) = 0. Se sugiere una primera aproximación de x=1 y seguidamente se aplica la fórmula de Newton-Raphson repetidamente hasta obtener una solución estable con 8 cifras decimales. Además, se motiva a los espectadores a intentar resolver otros problemas similares y se les anima a interactuar con el canal.
Takeaways
- 🔢 El vídeo enseña cómo calcular la raíz sexta de 2 con una precisión de 8 decimales.
- 📚 Se utiliza el método de Newton-Raphson para encontrar la aproximación.
- 📐 Se recomienda ver videos anteriores para comprender mejor este método.
- 🔍 Se define una función f(x) = x^6 - 2 para encontrar la raíz sexta de 2.
- 📉 Se calcula la derivada de la función f(x) = 6x^5 para el método de Newton-Raphson.
- 📌 Se sugiere que la primera aproximación puede ser x = 1 o x = 2.
- 🔄 Se aplica la fórmula de Newton-Raphson repetidamente para mejorar la aproximación.
- 🔄 Se obtiene x2, x3, x4, x5, x6 y x7 hasta que los decimales se mantienen fijos.
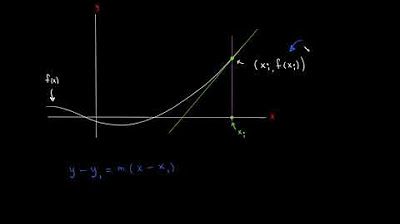
- 📊 Se enfatiza que el método de Newton-Raphson es útil para resolver ecuaciones donde se busca la intersección de funciones.
- 👍 Se anima a los espectadores a intentar el procedimiento por sí mismos y se invita a suscribirse y compartir el contenido.
Q & A
¿Qué método se utiliza en el vídeo para calcular la raíz sexta de 2 con 8 cifras decimales de precisión?
-Se utiliza el método de Newton-Raphson para calcular la raíz sexta de 2 con la precisión requerida.
¿Cuál es la función f(x) que se usa en el método de Newton-Raphson para encontrar la raíz sexta de 2?
-La función f(x) utilizada es f(x) = x^6 - 2, donde se busca el valor de x que haga que f(x) sea igual a 0.
¿Cómo se determina la derivada de la función f(x) = x^6 - 2 para aplicar el método de Newton-Raphson?
-La derivada de la función f(x) = x^6 - 2 es f'(x) = 6x^5.
¿Cuál es la primera aproximación de x que se toma en el vídeo para calcular la raíz sexta de 2?
-La primera aproximación de x que se toma es 1.
¿Cuál es la fórmula que se aplica repetidamente en el método de Newton-Raphson para mejorar la aproximación de x?
-La fórmula aplicada repetidamente es x_n+1 = x_n - f(x_n) / f'(x_n).
¿Cuál es el resultado de f(1) en la función f(x) = x^6 - 2?
-El resultado de f(1) es 1^6 - 2, que es -1.
¿Cuál es el resultado de f(2) en la función f(x) = x^6 - 2?
-El resultado de f(2) es 2^6 - 2, que es 64 - 2, dando como resultado 62.
¿Dónde debe estar el resultado de la raíz sexta de 2 si se prueba con valores entre 1 y 2?
-El resultado de la raíz sexta de 2 debe estar entre 1 y 2, ya que 1^6 = 1 y 2^6 = 64, y se busca un número cuya sexta potencia sea 2.
¿Cuál es la importancia de que los últimos decimales se queden fijos en el proceso de Newton-Raphson?
-La importancia de que los últimos decimales se queden fijos indica que ya se ha alcanzado una aproximación con la precisión deseada, en este caso, 8 cifras decimales.
¿Cómo se puede generalizar el método de Newton-Raphson para resolver otras ecuaciones no necesariamente exponenciales?
-El método de Newton-Raphson puede generalizarse para resolver otras ecuaciones al seguir el mismo procedimiento: pasar todos los términos al lado izquierdo para que quede igual a 0, calcular la derivada, elegir una primera aproximación y aplicar repetidamente la fórmula hasta alcanzar la precisión deseada.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)