Introduction to the unit circle | Trigonometry | Khan Academy
Summary
TLDRThe script explains the concept of a unit circle and its relation to trigonometric functions. It defines a unit circle as one with a radius of 1, centered at the origin, and describes the coordinates where it intersects the x and y axes. The video introduces the convention for measuring angles in a counterclockwise direction as positive and clockwise as negative. It then uses the unit circle to redefine cosine and sine in terms of the x and y coordinates of the intersection point of an angle's terminal side with the circle, extending the traditional definitions of trigonometric functions beyond right triangles.
Takeaways
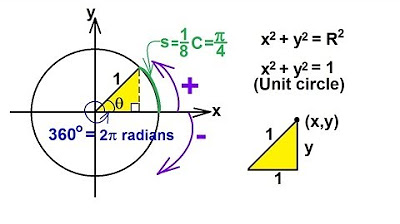
- 🌐 The video discusses the concept of a unit circle, which is a circle with a radius of 1 centered at the origin.
- 📍 The coordinates where the unit circle intersects the x-axis are (1, 0), (0, 1), (-1, 0), and (0, -1).
- 🔄 The video introduces a convention for measuring angles in the unit circle, with positive angles measured counterclockwise from the positive x-axis.
- 📊 The script explains how to use the unit circle to extend the definitions of trigonometric functions beyond right triangles.
- 📐 By constructing a right triangle within the unit circle, the video shows that the hypotenuse is always 1, the opposite side is the y-coordinate of the intersection point, and the adjacent side is the x-coordinate.
- 🌟 The cosine of an angle (θ) is defined as the x-coordinate (a) of the intersection point of the terminal side of the angle with the unit circle.
- 🌊 The sine of an angle (θ) is defined as the y-coordinate (b) of the intersection point of the terminal side of the angle with the unit circle.
- 🔄 The tangent of an angle (θ) is defined as the ratio of the sine to the cosine, which corresponds to the y-coordinate over the x-coordinate of the intersection point.
- 🚧 The traditional SOHCAHTOA definitions of trigonometric functions break down at angles of 0 or 90 degrees and above, but the unit circle definition does not.
- 📚 The video concludes by setting up a new definition for trigonometric functions using the unit circle that is consistent with SOHCAHTOA but extends its applicability.
Q & A
What is a unit circle?
-A unit circle is a circle with a radius of 1, centered at the origin of a coordinate system.
What are the coordinates of the points where the unit circle intersects the x-axis?
-The coordinates of the points where the unit circle intersects the x-axis are (1, 0) and (-1, 0).
What are the coordinates of the point where the unit circle intersects the y-axis?
-The coordinates of the point where the unit circle intersects the y-axis are (0, 1) and (0, -1).
What is the significance of defining angles in a counterclockwise direction?
-Defining angles in a counterclockwise direction establishes a positive direction for measuring angles, which is a common convention in mathematics.
How does the script define a positive angle?
-A positive angle is defined as an angle measured in a counterclockwise direction from the positive x-axis.
What is the relationship between the coordinates of a point on the unit circle and the trigonometric functions sine and cosine?
-The x-coordinate of a point where the terminal side of an angle intersects the unit circle is equal to the cosine of that angle, and the y-coordinate is equal to the sine of that angle.
What is the hypotenuse of the right triangle formed by dropping a perpendicular from a point on the unit circle to the x-axis?
-The hypotenuse of the right triangle formed in this way is the radius of the unit circle, which has a length of 1.
How does the script extend the traditional definitions of trigonometric functions?
-The script extends the traditional definitions of trigonometric functions by associating them with the coordinates of points on the unit circle, regardless of the angle being acute, right, or obtuse.
What is the definition of tangent in the context of the unit circle?
-The tangent of an angle, in the context of the unit circle, is defined as the ratio of the y-coordinate to the x-coordinate of the point where the terminal side of the angle intersects the unit circle.
Why might the traditional SOHCAHTOA definitions break down at certain angles?
-The traditional SOHCAHTOA definitions might break down at angles of 0 degrees, 90 degrees, or more, or negative angles because these cannot be represented as part of a right triangle.
How does the unit circle help in evaluating trigonometric ratios for angles greater than 90 degrees?
-The unit circle allows for the evaluation of trigonometric ratios for angles greater than 90 degrees by considering the coordinates of the intersection points of the terminal side of the angle with the unit circle.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
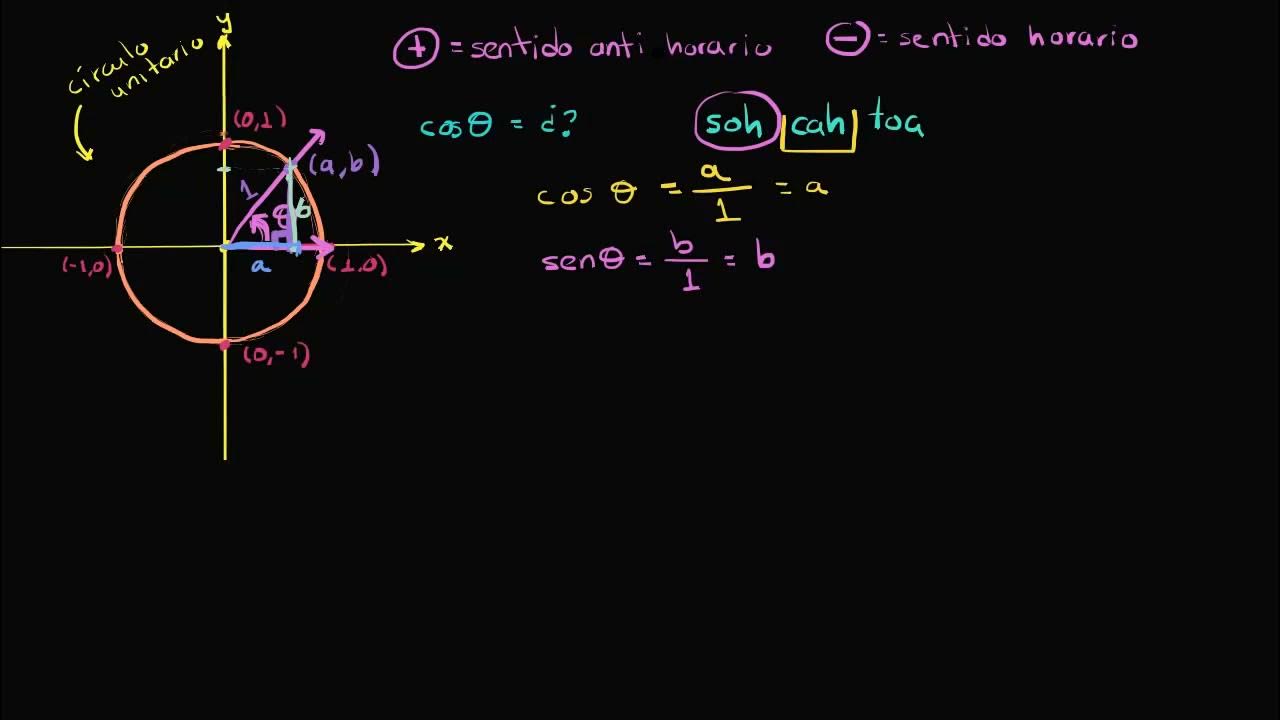
Círculo unitario. Definición de funciones trigonométricas

De eenheidscirkel (HAVO wiskunde B)

Tanda Fungsi Trigonometri Tiap Kuadran | Matematika Tingkat Lanjut SMA Kelas XI Kurikulum Merdeka
TRIGONOMETRY 1 (PRECALCULUS) (1 of 54) What Is The Unit Circle?

Circunferência trigonométrica

Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
5.0 / 5 (0 votes)
