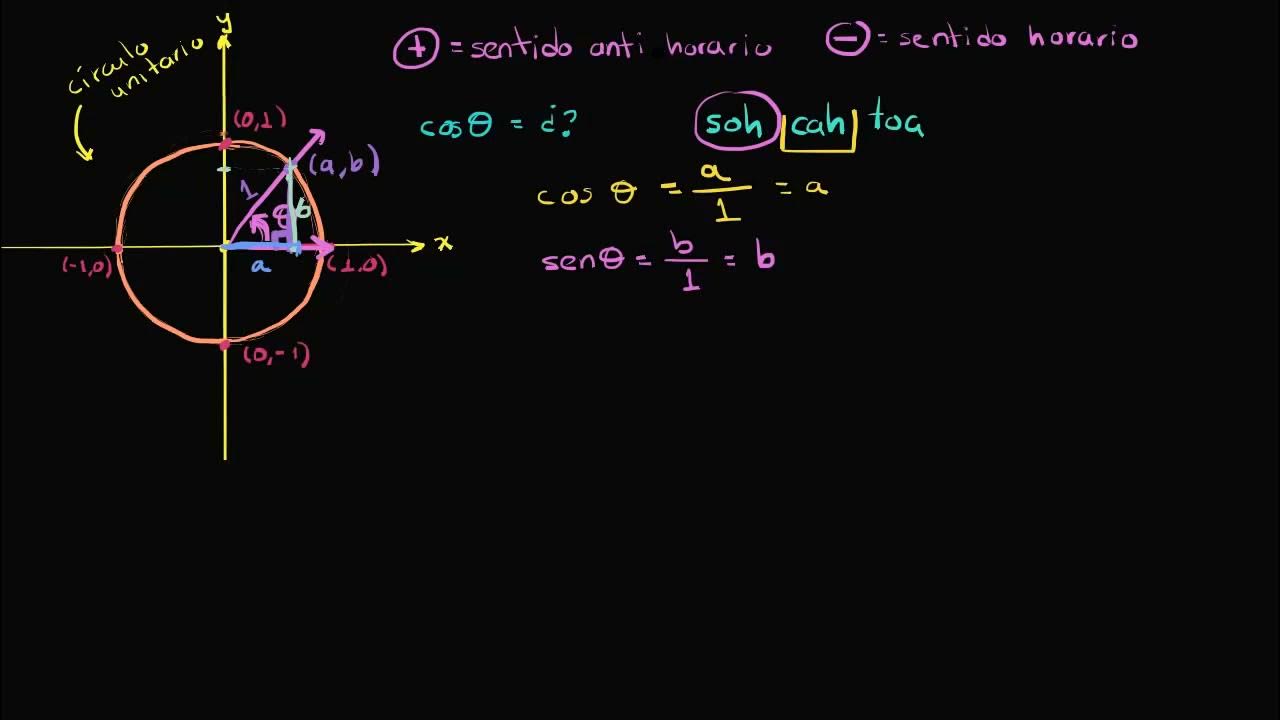Circunferência trigonométrica

Summary

In this video, Professor Kit Guedes explores the concept of the trigonometric circle, focusing on its key characteristics. She covers topics such as the circle's radius of 1 unit, the division into quadrants, and the direction of angle measurement (counterclockwise for positive angles and clockwise for negative ones). The video introduces radian measures and their equivalents in degrees, discusses congruent arcs, and explains how to divide the circle into smaller parts. Additionally, it delves into the application of these concepts in solving trigonometric equations, with a look at both positive and negative angles, including multiple rotations around the circle.

Takeaways

• 😀 The trigonometric circle has a radius of 1, with two perpendicular axes intersecting at its center, forming four quadrants.
• 😀 The positive direction for measuring angles on the trigonometric circle is counterclockwise, while the negative direction is clockwise.
• 😀 360 degrees corresponds to 2π radians, and 180 degrees equals π radians.
• 😀 The key angles in radians on the circle are 0, π/2, π, 3π/2, and 2π.
• 😀 The circle can be divided into more than four parts, like 8, by dividing each quadrant into smaller arcs.
• 😀 Congruent arcs are arcs that have the same image on the trigonometric circle, even if they result from multiple rotations.
• 😀 The circle is divided into quadrants: 1st, 2nd, 3rd, and 4th, numbered counterclockwise starting from the positive x-axis.
• 😀 Negative angles represent clockwise rotation from the origin, such as -5π/4, which involves moving five half-quadrants clockwise.
• 😀 Arcs of notable angles, like π/3, π/4, and π/6, help in precisely measuring and visualizing angles on the circle.
• 😀 Multiple rotations, like 4π or 6π radians, correspond to complete rotations and land back at the origin, demonstrating the periodicity of the trigonometric circle.
• 😀 The concepts of congruent arcs and periodicity are crucial when solving trigonometric equations, as they help identify all possible solutions.

Q & A

What is the radius of the trigonometric circle?

The radius of the trigonometric circle is 1 unit, often referred to as 'one unit' in the script.

What are the two axes in the trigonometric circle, and where do they intersect?

The two axes in the trigonometric circle are perpendicular to each other and pass through the center of the circle. Their intersection is the center of the circle.

What direction is considered positive when measuring angles on the trigonometric circle?

The positive direction for measuring angles is counterclockwise (anti-clockwise).

What is the relationship between degrees and radians for the full circle?

A full circle is 360 degrees or 2π radians. Therefore, 180 degrees corresponds to π radians.

How do you represent common angle values in radians on the trigonometric circle?

Common angle values include: 0 radians (0°), π/2 radians (90°), π radians (180°), 3π/2 radians (270°), and 2π radians (360°).

What are congruent arcs, and why are they important in the trigonometric circle?

Congruent arcs are arcs that have the same terminal point on the trigonometric circle. This concept is important for understanding how angles relate to each other, particularly when solving trigonometric equations.

What are the quadrants in the trigonometric circle, and how are they numbered?

The trigonometric circle is divided into four quadrants, numbered in the counterclockwise direction starting from the origin: first quadrant, second quadrant, third quadrant, and fourth quadrant.

How do you divide the circle into more than four sections, and what does this help with?

To divide the circle into more than four sections, you can split each quadrant into smaller parts, such as dividing it into 8 equal parts. This allows for more precise measurements of angles in radians, such as π/8 increments.

What happens when you move clockwise to mark negative angles?

When marking negative angles, you move clockwise from the origin. For example, a negative angle like -5π/4 involves moving clockwise five times the increment of π/4.

How is a complete rotation of the trigonometric circle expressed in radians?

A complete rotation around the circle is represented by 2π radians, and multiple rotations can be expressed as n times 2π, where n is an integer.