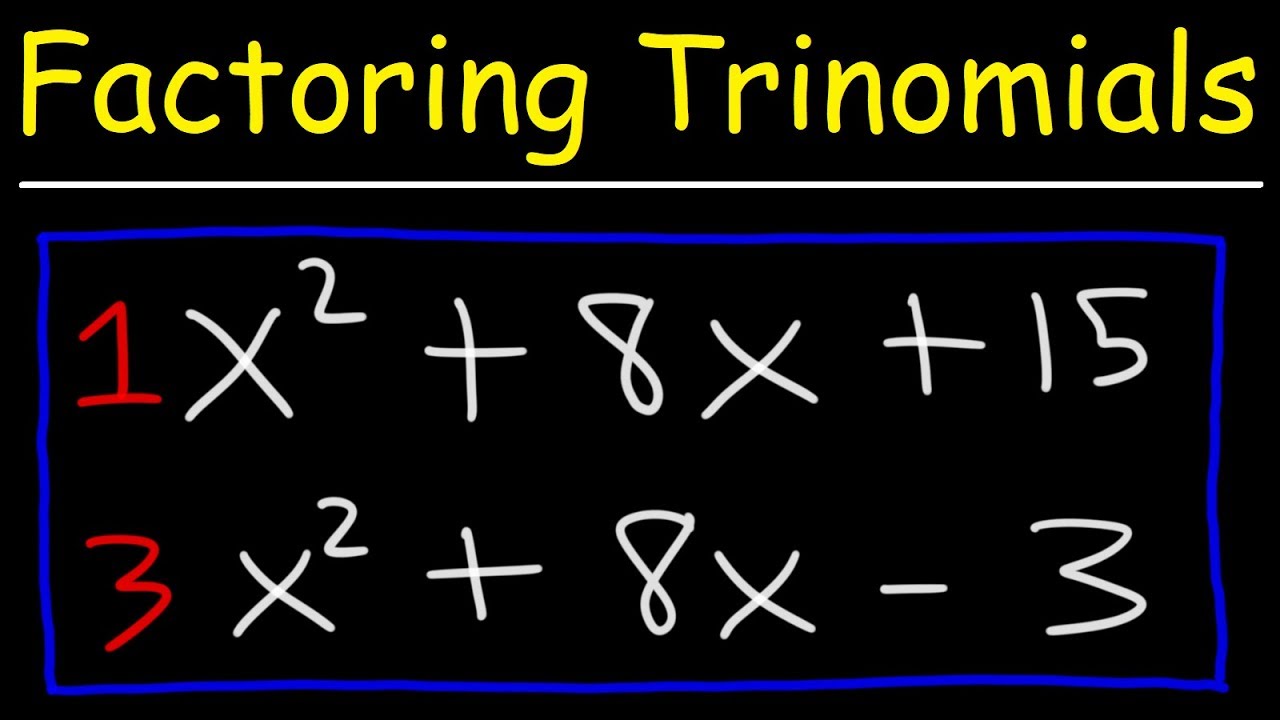
Factoring Trinomials
Summary
TLDRThis video introduces a unique method for factoring trinomials where the leading coefficient is not 1, a technique that may be unfamiliar to some. The presenter walks through two examples, demonstrating how to factor trinomials by multiplying the leading coefficient with the constant, finding factor pairs, and adjusting them to fit the equation. The video highlights the importance of reducing fractions and multiplying the denominators back into the equation. It's a helpful tutorial for students aiming to improve their factoring skills, especially for U.S. standardized tests.
Takeaways
- 🔢 Factoring trinomials with a leading coefficient greater than 1 can be done using a method not commonly taught in schools.
- 🧮 To start, multiply the leading coefficient by the constant value, transforming the equation.
- 🧑🏫 Factor the transformed trinomial by identifying two numbers that multiply to the product and add up to the middle term.
- ✅ Once the numbers are identified, create binomials for factoring.
- ➗ Divide the coefficients of the binomials by the original leading coefficient.
- 🔄 Simplify the fractions and then multiply the denominators to the variable.
- 📐 Verify the factored form by multiplying it back to the original trinomial to check for correctness.
- 🧩 In examples with negative values, use different signs in the binomials based on whether the constant is negative.
- 🔍 For subtraction cases, find pairs of numbers that subtract to give the middle term.
- 📊 Final step: multiply out the factored binomials to confirm the accuracy of the original trinomial.
Q & A
What is the first step in factoring a trinomial with a leading coefficient not equal to one?
-The first step is to multiply the leading coefficient by the constant term. For example, in the expression 12x² + 17x + 6, you multiply 12 by 6, resulting in 72.
How do you factor the expression after multiplying the leading coefficient with the constant?
-After multiplying, rewrite the expression as a trinomial with x². For example, 12x² + 17x + 6 becomes x² + 17x + 72. Then factor it by finding two numbers that multiply to the constant and add to the middle term.
How do you determine the two numbers when factoring the trinomial?
-You list pairs of numbers that multiply to the constant (72 in the first example). Then, find the pair that adds up to the middle term's coefficient (17 in this case). For 72, the correct pair is 8 and 9 because 8 + 9 = 17.
Why do you divide the factored terms by the original leading coefficient?
-You divide by the original leading coefficient (12 in this case) because earlier, you multiplied the leading coefficient to simplify the trinomial. Dividing helps balance the equation and return it to its correct form.
What do you do with the fractions after dividing the factored terms?
-You reduce the fractions if possible. For example, after dividing by 12, you get terms like 2/3 and 3/4. Next, you multiply the denominators to the x terms in each factor.
How do you handle negative constants in trinomials?
-When the constant is negative, like in x² - 5x - 24, you use one positive and one negative sign in the factors because the constant term determines the signs in the factor pairs.
What is the process for factoring trinomials with opposite signs in the factors?
-You need to find two numbers that subtract to the middle term's coefficient. For example, to factor x² - 5x - 24, you find numbers that multiply to -24 and subtract to -5. The correct pair is 8 and -3.
How do you determine which factor gets the negative sign?
-The larger number is paired with the negative sign if the middle term is negative. For instance, with -5x, you place the -8 in the factor that corresponds with x, and the +3 goes in the other factor.
What happens after you factor a trinomial with negative constants?
-You divide the factored terms by the original leading coefficient, reduce the fractions, and then multiply the denominators back into the x terms.
How can you verify the factored form is correct?
-You can verify the factored form by multiplying the factors back out to see if you get the original trinomial. For example, multiplying (2x + 1)(3x - 4) should give you the original 6x² - 5x - 4.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)