Factoring Tough Trinomials Using the Box Method
Summary
TLDRThis video introduces the 'Box Method' for factoring trinomials, an alternative to the AC method. It simplifies the process by eliminating the need for factor by grouping. The method involves setting up a box with the quadratic term in the upper left, the constant in the lower right, and the middle terms derived from the product of 'a' and 'c' and the sum of 'b'. The video demonstrates the method with examples, showing how to find the middle terms and factor the trinomial into binomials. It's particularly useful for trinomials where 'a' is not 1, offering a clear and straightforward approach to factorization.
Takeaways
- 📚 The video introduces the 'Box Method' for factoring trinomials, which is a variation of the AC method.
- 🔍 The Box Method simplifies the process by eliminating the need for factor by grouping, which can be confusing for some.
- 📐 The method begins by writing the trinomial in descending order of powers, ensuring the equation is set up correctly.
- 🔢 The 'a' and 'c' values from the trinomial are multiplied to get the product, AC, and then two numbers are found that multiply to AC and add up to B.
- 📈 A box is set up with 'a' in the upper left, the constant 'c' in the lower right, and the two numbers found for the B value in the other two corners, each with an 'x'.
- 🔄 The trinomial's middle term is split into two terms that correspond to the numbers in the box, ensuring each has an 'x'.
- 🧩 The greatest common factor (GCF) of each row in the box is determined, which will correspond to the factors outside the box.
- 🔄 The GCFs from the rows are used to find the factors on the sides of the box, which when multiplied together, give the original trinomial.
- 🔍 The method is demonstrated through examples, showing how to factor trinomials like 9x^2 - 21x - 8 and 6x^2 + 13x - 5.
- 📝 The video emphasizes that the Box Method is particularly useful when 'a' is not 1, as it simplifies the factoring process for more complex trinomials.
Q & A
What is the primary focus of the video?
-The video focuses on teaching a method for factoring trinomials called the 'Box Method,' which is a variation of the AC method.
Why might the Box Method be preferred over the AC method?
-The Box Method might be preferred because it eliminates the factor by grouping step, which can be confusing for some people.
What is the first step in factoring a trinomial using the Box Method?
-The first step is to write the trinomial in descending order of powers.
What are the roles of 'a', 'b', and 'c' in the context of the Box Method?
-In the Box Method, 'a' is the coefficient of the x squared term, 'b' is the coefficient of the x term, and 'c' is the constant term.
How does the Box Method simplify the process of finding the two numbers that multiply to 'ac' and add up to 'b'?
-The Box Method simplifies this process by visually organizing the numbers in a box, which helps in identifying the two numbers more intuitively.
What is the significance of placing the x squared term and the constant term in specific corners of the box?
-The x squared term is placed in the upper left corner, and the constant term in the lower right corner of the box to set up the structure for factoring.
Why is it important to include 'x' in the two middle boxes of the Box Method?
-Including 'x' in the two middle boxes is crucial because it represents the terms that will be factored out from the trinomial.
How does the Box Method ensure that the factors are correctly identified?
-The Box Method ensures correct factor identification by using the greatest common factor of each row and checking that the products of these factors match the original trinomial.
What is the purpose of the greatest common factor (GCF) in the Box Method?
-The GCF is used to simplify each row of the box, making it easier to identify the binomial factors that will multiply to give the original trinomial.
How can one verify that the factors obtained using the Box Method are correct?
-One can verify the factors by using the FOIL method (First, Outer, Inner, Last) to multiply the binomials and check if they result in the original trinomial.
Is the Box Method suitable for all types of trinomials, or are there specific conditions for its use?
-The Box Method is suitable for most trinomials, but it is particularly effective when the coefficient 'a' of the x squared term is not 1, as it simplifies the process of finding the correct factors.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

ATHS Factoring General Trinomial

Factoring Trinomials using the AC Method

How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course

2. Ecuaciones cuadráticas completas, solución por el Método de completar el binomio
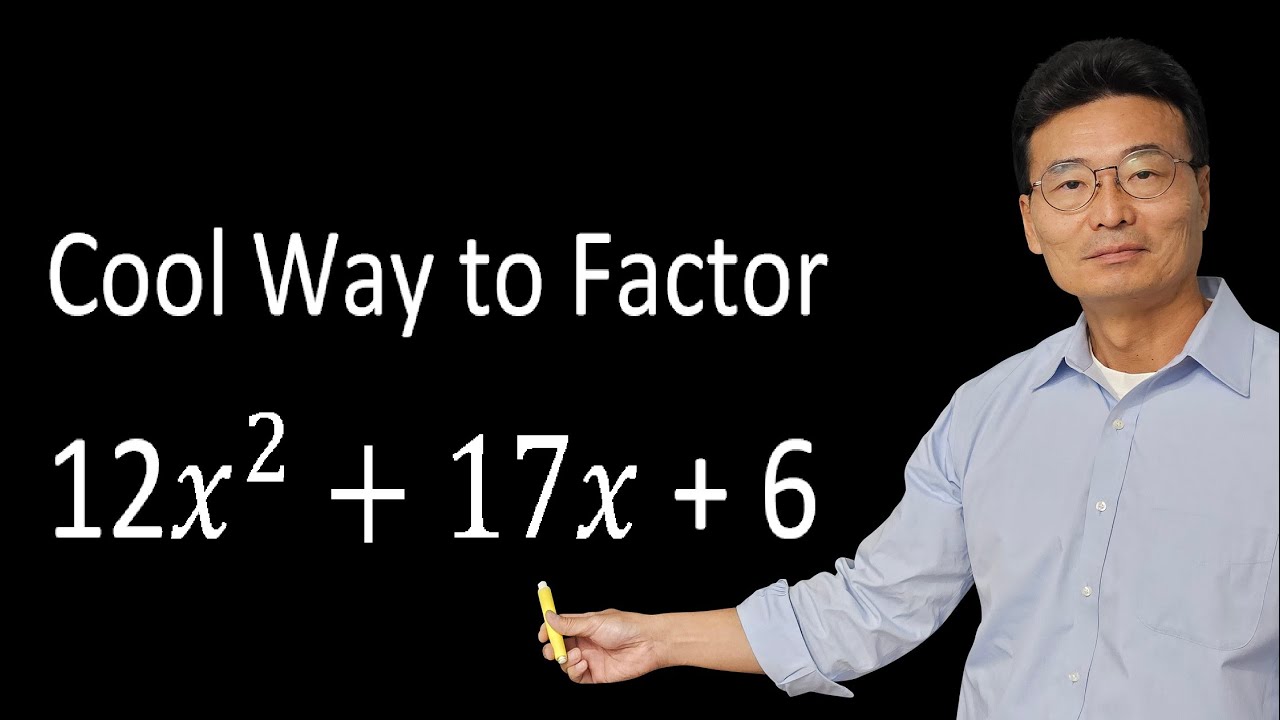
Factoring Trinomials
Factoring Trinomials The Easy Fast Way
5.0 / 5 (0 votes)